1.3 探索三角形全等的条件 第1课时课件 (共27张PPT) 2023-2024学年苏科版数学八年级上册
文档属性
| 名称 | 1.3 探索三角形全等的条件 第1课时课件 (共27张PPT) 2023-2024学年苏科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
1 . 3
探索三角形全等的条件
第1课时
利用两边夹角判定三角形全等
讨 论
1.当两个三角形的1对边或角相等时,它们全等吗
2.当两个三角形的2对边或角分别相等时,它们全等吗
当两个三角形的1对边或角相等时,它们不一定全等.
当两个三角形的2对边或角分别相等时,它们不一定全等.
3. 当两个三角形的3对边或角分别相等时,它们全等吗
当两个三角形的 3 对边分别相等时,它们一定全等;
当两个三角形的3 对角分别相等时,它们不一定全等.
交 流
1. 如图,每人用一张长方形纸剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合
剪下的所有直角三角形的两条直角边分别相等或斜边和一条直角边分别相等,则它们都能够重合。
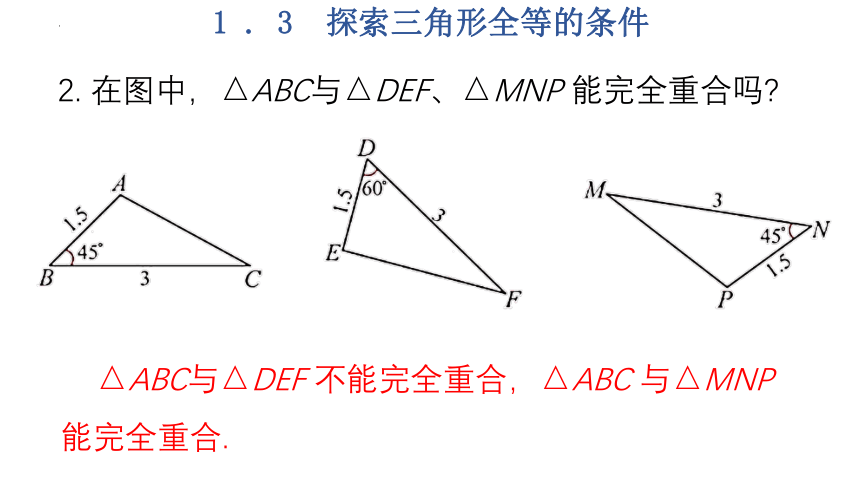
2. 在图中,△ABC与△DEF、△MNP 能完全重合吗
△ABC与△DEF 不能完全重合,△ABC 与△MNP 能完全重合.
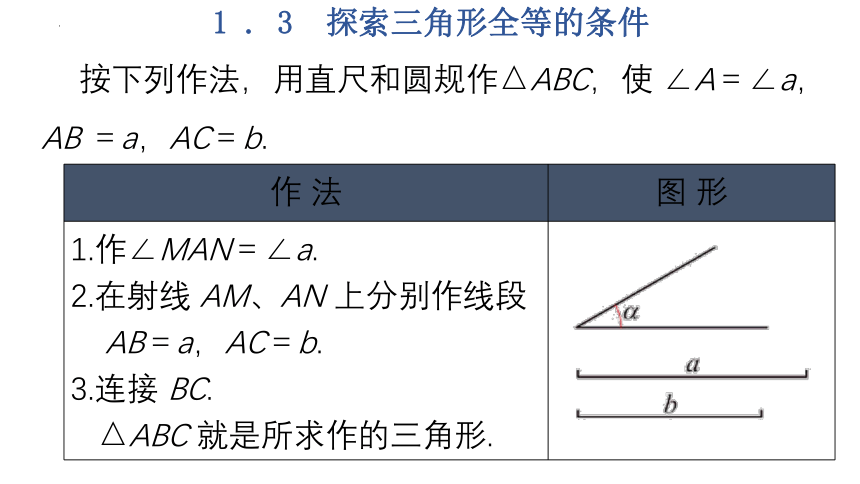
按下列作法,用直尺和圆规作△ABC,使 ∠A=∠a,AB =a,AC=b.
作 法 图 形
1.作∠MAN=∠a. 2.在射线 AM、AN 上分别作线段 AB=a,AC=b. 3.连接 BC. △ABC 就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗
实践告诉我们判定两个三角形全等的一个基本事实:
两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
书写格式:
如图,在△ABC和△A′B′C′中,
AB=A′B′,
∵ ∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′ ( SAS).
相等的元素:两边及其夹角.
2. 书写顺序:边→角→边.
3. 两边和其中一边的对角分别相等的两个三角形不
一定全等.
要点提醒:
例1 已知:如图,AB=AD,∠BAC=∠DAC.
求证:△ABC≌△ADC.
证明:在△ABC 和△ADC 中,
AB=AD(已知),
∠BAC=∠DAC(已知),
AC=AC(公共边),
∴ △ABC≌ △ADC(SAS).
其中一个三角形沿AC所在直线翻折后,能与另一个三角形重合.
已知:如图,C 是AB 的中点,AD=CE,
且AD∥CE.
求证:△ACD ≌△CBE.
练1
解题秘方:先根据条件找出两个三角形中的两条边及
其夹角对应相等,再根据“SAS”判定两
个三角形全等.
常见的隐含等角的情况:
① 公共角相等; ②对顶角相等;
③ 等角加(或减)等角,其和(或差)仍相等;
④同角或等角的余( 或补) 角相等;
⑤ 由角平分线的定义得出角相等;
⑥由垂直的定义得出角相等;
⑦ 由平行线得到同位角或内错角相等.
方法点拨:
证明:∵ C 是AB 的中点(已知),
∴ AC=CB(线段中点的定义).
∵ AD ∥ CE(已知),
∴∠CAD=∠BCE(两直线平行,同位角相等).
在△ ACD 和△ CBE 中,
AC=CB(已证),
∠CAD=∠BCE(已证),
AD=CE(已知),
∴ △ACD ≌△CBE(SAS).
读一读
图形的运动与“SAS”
本节中,我们知道了判定两个三角形全等的一个基本事实——两边及其夹角分别相等的两个三角形全等(SAS). 其实,我们可以用图形运动的方法来确认它的正确性.
如图(1),在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,BC=B′C′.
把△ABC叠合到△A′B′C′上,使 BC与B′C′重合,∠B、∠B′落在 BC的同一侧.
因为 ∠B=∠B,所以BA 落在射线B′A′上。又因为 BA=B′A′,所以点A 与点A′重合.根据“两点确定一条直线”,可以知道AC与A′C′重合。于是△ABC与△A′B′C′ 重合(如图(2)),即 △ABC≌△A′B′C′.
试仿照上面的方法,证实本节例 1中的结论.
例2 已知:如图1-8,AB、CD 相交于点E,且E是AB、
CD 的中点.
求证:△AEC≌△BED.
证明:∵E是AB、CD的中点(已知),
∴ AE=BE,CE=DE
(线段中点的定义).
在△AEC和△BED中,
AE=BE(已证),
∠AEC=∠BED(对顶角相等)
CE=DE(已证),
∴△AEC≌△BED(SAS)
其中一个三角形绕点E旋转180°后,能与另一个三角形重合.
你能证明图中AC∥DB 吗
讨 论
能. 证明如下:
∵△AEC≌△BED(已证),
∴∠A=∠B(全等三角形的对应角相等),
∴AC∥DB (内错角相等,两直线平行)
(注:证明△AEC≌△BED 的过程同例 2)
例3 已知:如图,点E、F在CD上,且CE=DF,AE=BF,
AE∥BF.
求证:△AEC ≌△BFD.
证明:∵AE // BF (已知),
∴∠AEC=∠BFD
(两直线平行,内错角相等).
在△AEC 和△BFD 中,
AE=BF(已知),
∠AEC=∠BFD(已证),
CE=DF(已知),
∴△AEC≌△BFD(SAS).
能否改变图1-9中△AEC的位置得到图1-8?
图1-9
图1-8
讨 论
根据 例3 中的已知条件,你还能证得其他新的结论吗
根据例3中的已知条件,还能证得结论:
①∠A=∠B;②∠C=∠D;
③ CF=DE; ④AC=BD;⑤AC∥BD等.
如证明 AC∥BD 过程如下:
∵△AEC≌△BFD (已证),
∴ ∠C=∠D (全等三角形的对应角相等).
∴AC∥BD (内错角相等,两直线平行)
(注:证明△AEC≌△BFD 的过程同例 3)
本课小结
利用两边夹角判定三角形全等
(1) 本节课学习了哪些主要内容?
(2) 我们是怎么探究出“SAS”判定方法的?用“SAS”
判定三角形全等应注意什么问题?
(3) 到现在为止,你学到了几种证明两个三角形全等的
方法?
1 . 3
探索三角形全等的条件
第1课时
利用两边夹角判定三角形全等
讨 论
1.当两个三角形的1对边或角相等时,它们全等吗
2.当两个三角形的2对边或角分别相等时,它们全等吗
当两个三角形的1对边或角相等时,它们不一定全等.
当两个三角形的2对边或角分别相等时,它们不一定全等.
3. 当两个三角形的3对边或角分别相等时,它们全等吗
当两个三角形的 3 对边分别相等时,它们一定全等;
当两个三角形的3 对角分别相等时,它们不一定全等.
交 流
1. 如图,每人用一张长方形纸剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合
剪下的所有直角三角形的两条直角边分别相等或斜边和一条直角边分别相等,则它们都能够重合。
2. 在图中,△ABC与△DEF、△MNP 能完全重合吗
△ABC与△DEF 不能完全重合,△ABC 与△MNP 能完全重合.
按下列作法,用直尺和圆规作△ABC,使 ∠A=∠a,AB =a,AC=b.
作 法 图 形
1.作∠MAN=∠a. 2.在射线 AM、AN 上分别作线段 AB=a,AC=b. 3.连接 BC. △ABC 就是所求作的三角形.
你作的三角形与其他同学作的三角形能完全重合吗
实践告诉我们判定两个三角形全等的一个基本事实:
两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
书写格式:
如图,在△ABC和△A′B′C′中,
AB=A′B′,
∵ ∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′ ( SAS).
相等的元素:两边及其夹角.
2. 书写顺序:边→角→边.
3. 两边和其中一边的对角分别相等的两个三角形不
一定全等.
要点提醒:
例1 已知:如图,AB=AD,∠BAC=∠DAC.
求证:△ABC≌△ADC.
证明:在△ABC 和△ADC 中,
AB=AD(已知),
∠BAC=∠DAC(已知),
AC=AC(公共边),
∴ △ABC≌ △ADC(SAS).
其中一个三角形沿AC所在直线翻折后,能与另一个三角形重合.
已知:如图,C 是AB 的中点,AD=CE,
且AD∥CE.
求证:△ACD ≌△CBE.
练1
解题秘方:先根据条件找出两个三角形中的两条边及
其夹角对应相等,再根据“SAS”判定两
个三角形全等.
常见的隐含等角的情况:
① 公共角相等; ②对顶角相等;
③ 等角加(或减)等角,其和(或差)仍相等;
④同角或等角的余( 或补) 角相等;
⑤ 由角平分线的定义得出角相等;
⑥由垂直的定义得出角相等;
⑦ 由平行线得到同位角或内错角相等.
方法点拨:
证明:∵ C 是AB 的中点(已知),
∴ AC=CB(线段中点的定义).
∵ AD ∥ CE(已知),
∴∠CAD=∠BCE(两直线平行,同位角相等).
在△ ACD 和△ CBE 中,
AC=CB(已证),
∠CAD=∠BCE(已证),
AD=CE(已知),
∴ △ACD ≌△CBE(SAS).
读一读
图形的运动与“SAS”
本节中,我们知道了判定两个三角形全等的一个基本事实——两边及其夹角分别相等的两个三角形全等(SAS). 其实,我们可以用图形运动的方法来确认它的正确性.
如图(1),在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,BC=B′C′.
把△ABC叠合到△A′B′C′上,使 BC与B′C′重合,∠B、∠B′落在 BC的同一侧.
因为 ∠B=∠B,所以BA 落在射线B′A′上。又因为 BA=B′A′,所以点A 与点A′重合.根据“两点确定一条直线”,可以知道AC与A′C′重合。于是△ABC与△A′B′C′ 重合(如图(2)),即 △ABC≌△A′B′C′.
试仿照上面的方法,证实本节例 1中的结论.
例2 已知:如图1-8,AB、CD 相交于点E,且E是AB、
CD 的中点.
求证:△AEC≌△BED.
证明:∵E是AB、CD的中点(已知),
∴ AE=BE,CE=DE
(线段中点的定义).
在△AEC和△BED中,
AE=BE(已证),
∠AEC=∠BED(对顶角相等)
CE=DE(已证),
∴△AEC≌△BED(SAS)
其中一个三角形绕点E旋转180°后,能与另一个三角形重合.
你能证明图中AC∥DB 吗
讨 论
能. 证明如下:
∵△AEC≌△BED(已证),
∴∠A=∠B(全等三角形的对应角相等),
∴AC∥DB (内错角相等,两直线平行)
(注:证明△AEC≌△BED 的过程同例 2)
例3 已知:如图,点E、F在CD上,且CE=DF,AE=BF,
AE∥BF.
求证:△AEC ≌△BFD.
证明:∵AE // BF (已知),
∴∠AEC=∠BFD
(两直线平行,内错角相等).
在△AEC 和△BFD 中,
AE=BF(已知),
∠AEC=∠BFD(已证),
CE=DF(已知),
∴△AEC≌△BFD(SAS).
能否改变图1-9中△AEC的位置得到图1-8?
图1-9
图1-8
讨 论
根据 例3 中的已知条件,你还能证得其他新的结论吗
根据例3中的已知条件,还能证得结论:
①∠A=∠B;②∠C=∠D;
③ CF=DE; ④AC=BD;⑤AC∥BD等.
如证明 AC∥BD 过程如下:
∵△AEC≌△BFD (已证),
∴ ∠C=∠D (全等三角形的对应角相等).
∴AC∥BD (内错角相等,两直线平行)
(注:证明△AEC≌△BFD 的过程同例 3)
本课小结
利用两边夹角判定三角形全等
(1) 本节课学习了哪些主要内容?
(2) 我们是怎么探究出“SAS”判定方法的?用“SAS”
判定三角形全等应注意什么问题?
(3) 到现在为止,你学到了几种证明两个三角形全等的
方法?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
