2.1.2 直线的倾斜角与斜率(含2课时)课件2023-2024学年高二数学(人教A版2019选择性必修第一册)(共28张PPT)
文档属性
| 名称 | 2.1.2 直线的倾斜角与斜率(含2课时)课件2023-2024学年高二数学(人教A版2019选择性必修第一册)(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 17:26:30 | ||
图片预览




文档简介
(共28张PPT)
在以往的几何学习中,我们常常通过直观感知、逻辑推理、度量计算等丰富研究几何图形中的形状、大小、位置关系。
十六世纪以后,由于生产和科学技术的发展,天文、力学、航海等方面都对几何学提出了新的需要。比如,德国天文学家开普勒发现行星是绕着太阳沿着椭圆轨道运行的,太阳处在这个椭圆的一个焦点上;意大利科学家伽利略发现投掷物体是沿着抛物线运动的。为了要精准地研究这些比较复杂的曲线,导致了解析几何的出现。
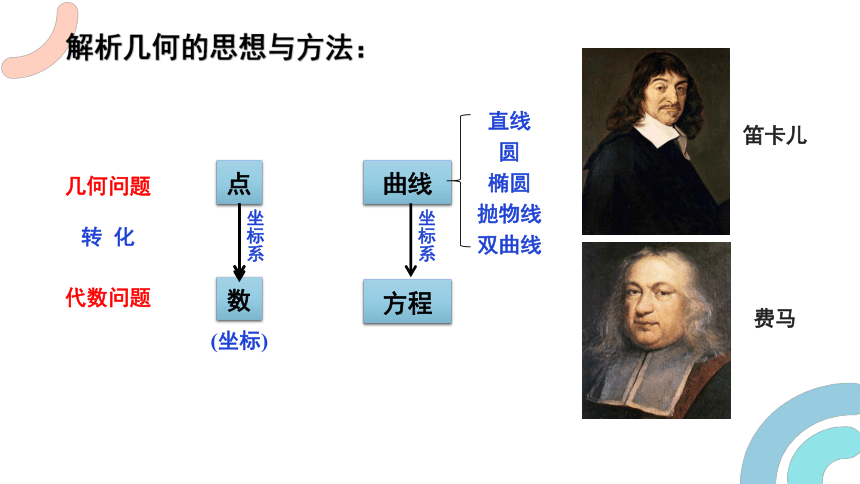
解析几何的思想与方法:
点
数
曲线
方程
坐标系
几何问题
代数问题
转 化
(坐标)
笛卡儿
费马
直线
圆
椭圆
抛物线
双曲线
坐标系
2.1.1 倾斜角与斜率
选择性必修第一册 第二章《直线和圆的方程》
问题1:如何确定一条直线的位置?
两点可确定一条直线
一点和一个方向可确定一条直线
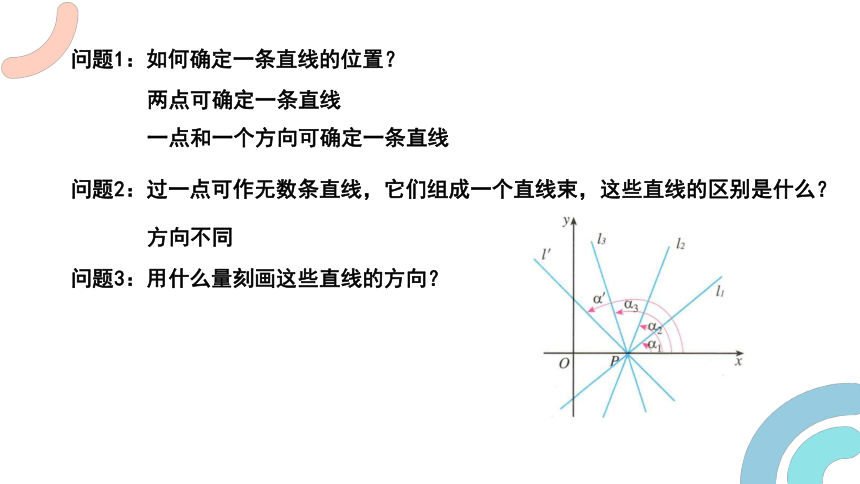
问题2:过一点可作无数条直线,它们组成一个直线束,这些直线的区别是什么?
方向不同
问题3:用什么量刻画这些直线的方向?
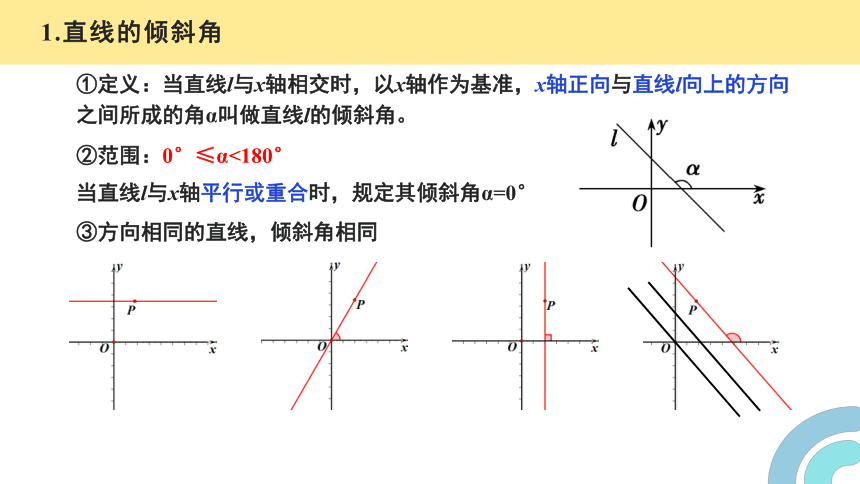
①定义:当直线l与x轴相交时,以x轴作为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角。
1.直线的倾斜角
②范围:0°≤α<180°
当直线l与x轴平行或重合时,规定其倾斜角α=0°
③方向相同的直线,倾斜角相同
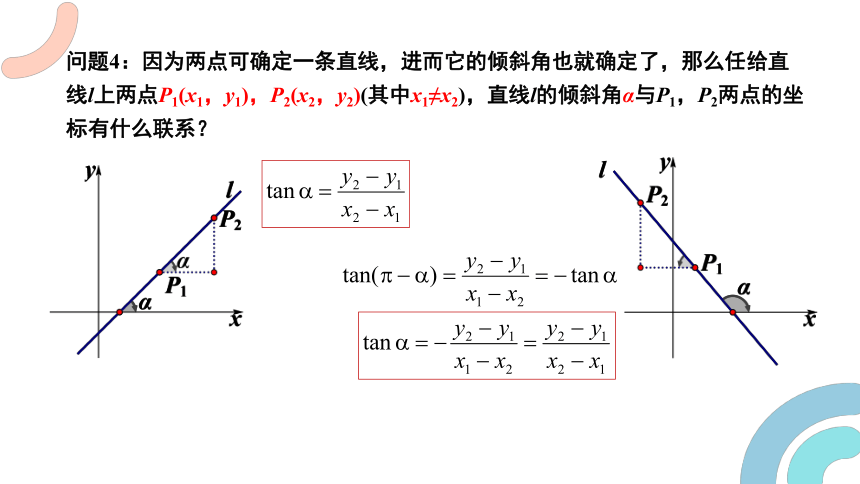
问题4:因为两点可确定一条直线,进而它的倾斜角也就确定了,那么任给直线l上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),直线l的倾斜角α与P1,P2两点的坐标有什么联系?
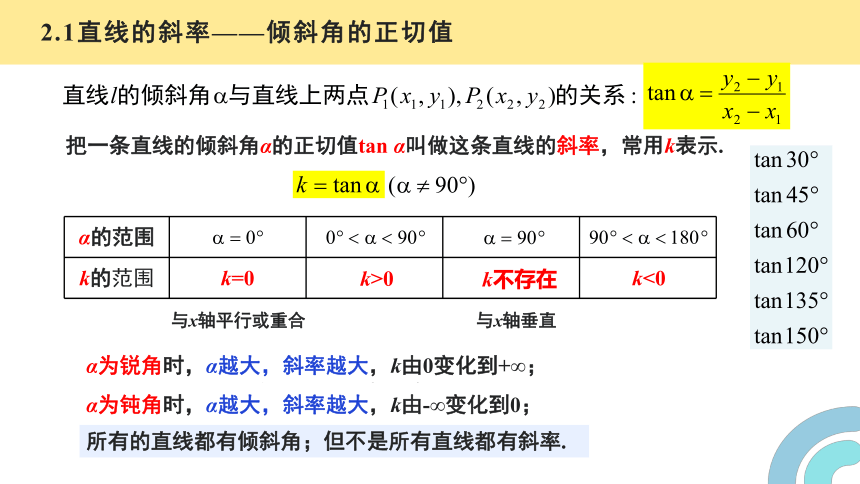
2.1直线的斜率——倾斜角的正切值
把一条直线的倾斜角α的正切值tan α叫做这条直线的斜率,常用k表示.
α的范围
k的范围 k=0
k>0
k不存在
k<0
与x轴垂直
与x轴平行或重合
直线的倾斜角越大,斜率越大( )
α为锐角时,α越大,斜率越大,k由0变化到+∞;
α为钝角时,α越大,斜率越大,k由-∞变化到0;
所有的直线都有倾斜角;但不是所有直线都有斜率.
2.2直线的斜率——两点坐标
基础练习——倾斜角与斜率的关系
基础练习——倾斜角与斜率的关系
4.(多选)若直线l的向上的方向与y轴的正方向成30°角,则直线l的倾斜角为( ).
A.30° B.60° C.120° D.150°
BC
例题讲解——求斜率或倾斜角的范围
例1.已知两点A(-3,4),B(3,2),直线l经过点P(2,-1) ,且与线段AB相交,则
l的斜率k的取值范围是________________.
[变式1]直线l过点P(1,0),且与以A(2,1),B(0,)为端点的线段有公共点,求直线l 的斜率k和倾斜角α的取值范围.
例题讲解——求斜率或倾斜角的范围
例2.(1)若直线l的倾斜角α满足45°<α<120°,求直线l的斜率k的取值范围.
(2)若直线l的斜率k满足k≥,求直线l的倾斜角α的取值范围.
(3)若直线l的斜率k满足k≤,求直线l的倾斜角α的取值范围.
(4)若直线l的斜率k满足﹣1知α求k或知k求α:
利用y=tan x的图象
2.1.2 两条直线平行和垂直的判定
选择性必修第一册 第二章《直线和圆的方程》
问题1:对于两条不重合的直线l1与l2,其倾斜角分别为α1与α2,斜率分别为k1,k2,若l1∥l2,α1与α2之间有什么关系?k1与k2之间有什么关系?
已知两条不重合的直线l1,l2,则“l1∥l2”是“两条直线斜率相等”的_________条件
必要不充分
1.两条直线平行的判定
对于斜率分别为k1,k2的两条直线l1,l2,
可用斜率相等证三点共线.
练习1.若三点A(2,1),B(﹣2,m),C(6,8)在同一条直线上,则m的值为______.
问题2:对于两条直线l1与l2,其方向向量分别为与,斜率分别为k1,k2,若l1⊥l2,与之间有什么关系?k1与k2之间有什么关系?
2.两条直线垂直的判定
对于斜率分别为k1,k2的两条直线l1,l2,
[例1]已知直线l1过点A(3,a),B(a-2,3),直线l2过点C(2,3),D(﹣1,a-2),
若l1⊥l2,求实数a的值.
2.两条直线垂直的判定
练习2.已知定点A(-1,3),B(4,2),以AB为直径作圆,与x轴有交点P,则交点P的坐标是 .
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
例2.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
例4.已知A(一6,0),B(3,6),P(0,3),Q(6,—6),试判断直线AB与PQ的位置关系.
例3.已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
例5.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习3.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A、B、C、D四点,试判定图形ABCD的形状.
直角梯形
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习3.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A、B、C、D四点,试判定图形ABCD的形状.
直角梯形
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习4.已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),则第四个顶点D的坐标为________.
练习5.已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,求点D的坐标.
题型点拨——用斜率关系判断直线的位置关系或形状
析:kAB=3,kBC=0
则kAB·kBC=0≠-1,即AB与BC不垂直
①由AD//BC,BC⊥CD求D
②由AB//DC,AB⊥AD求D
分类讨论思想
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
【小结】与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
在以往的几何学习中,我们常常通过直观感知、逻辑推理、度量计算等丰富研究几何图形中的形状、大小、位置关系。
十六世纪以后,由于生产和科学技术的发展,天文、力学、航海等方面都对几何学提出了新的需要。比如,德国天文学家开普勒发现行星是绕着太阳沿着椭圆轨道运行的,太阳处在这个椭圆的一个焦点上;意大利科学家伽利略发现投掷物体是沿着抛物线运动的。为了要精准地研究这些比较复杂的曲线,导致了解析几何的出现。
解析几何的思想与方法:
点
数
曲线
方程
坐标系
几何问题
代数问题
转 化
(坐标)
笛卡儿
费马
直线
圆
椭圆
抛物线
双曲线
坐标系
2.1.1 倾斜角与斜率
选择性必修第一册 第二章《直线和圆的方程》
问题1:如何确定一条直线的位置?
两点可确定一条直线
一点和一个方向可确定一条直线
问题2:过一点可作无数条直线,它们组成一个直线束,这些直线的区别是什么?
方向不同
问题3:用什么量刻画这些直线的方向?
①定义:当直线l与x轴相交时,以x轴作为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角。
1.直线的倾斜角
②范围:0°≤α<180°
当直线l与x轴平行或重合时,规定其倾斜角α=0°
③方向相同的直线,倾斜角相同
问题4:因为两点可确定一条直线,进而它的倾斜角也就确定了,那么任给直线l上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),直线l的倾斜角α与P1,P2两点的坐标有什么联系?
2.1直线的斜率——倾斜角的正切值
把一条直线的倾斜角α的正切值tan α叫做这条直线的斜率,常用k表示.
α的范围
k的范围 k=0
k>0
k不存在
k<0
与x轴垂直
与x轴平行或重合
直线的倾斜角越大,斜率越大( )
α为锐角时,α越大,斜率越大,k由0变化到+∞;
α为钝角时,α越大,斜率越大,k由-∞变化到0;
所有的直线都有倾斜角;但不是所有直线都有斜率.
2.2直线的斜率——两点坐标
基础练习——倾斜角与斜率的关系
基础练习——倾斜角与斜率的关系
4.(多选)若直线l的向上的方向与y轴的正方向成30°角,则直线l的倾斜角为( ).
A.30° B.60° C.120° D.150°
BC
例题讲解——求斜率或倾斜角的范围
例1.已知两点A(-3,4),B(3,2),直线l经过点P(2,-1) ,且与线段AB相交,则
l的斜率k的取值范围是________________.
[变式1]直线l过点P(1,0),且与以A(2,1),B(0,)为端点的线段有公共点,求直线l 的斜率k和倾斜角α的取值范围.
例题讲解——求斜率或倾斜角的范围
例2.(1)若直线l的倾斜角α满足45°<α<120°,求直线l的斜率k的取值范围.
(2)若直线l的斜率k满足k≥,求直线l的倾斜角α的取值范围.
(3)若直线l的斜率k满足k≤,求直线l的倾斜角α的取值范围.
(4)若直线l的斜率k满足﹣1
利用y=tan x的图象
2.1.2 两条直线平行和垂直的判定
选择性必修第一册 第二章《直线和圆的方程》
问题1:对于两条不重合的直线l1与l2,其倾斜角分别为α1与α2,斜率分别为k1,k2,若l1∥l2,α1与α2之间有什么关系?k1与k2之间有什么关系?
已知两条不重合的直线l1,l2,则“l1∥l2”是“两条直线斜率相等”的_________条件
必要不充分
1.两条直线平行的判定
对于斜率分别为k1,k2的两条直线l1,l2,
可用斜率相等证三点共线.
练习1.若三点A(2,1),B(﹣2,m),C(6,8)在同一条直线上,则m的值为______.
问题2:对于两条直线l1与l2,其方向向量分别为与,斜率分别为k1,k2,若l1⊥l2,与之间有什么关系?k1与k2之间有什么关系?
2.两条直线垂直的判定
对于斜率分别为k1,k2的两条直线l1,l2,
[例1]已知直线l1过点A(3,a),B(a-2,3),直线l2过点C(2,3),D(﹣1,a-2),
若l1⊥l2,求实数a的值.
2.两条直线垂直的判定
练习2.已知定点A(-1,3),B(4,2),以AB为直径作圆,与x轴有交点P,则交点P的坐标是 .
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
例2.已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
例4.已知A(一6,0),B(3,6),P(0,3),Q(6,—6),试判断直线AB与PQ的位置关系.
例3.已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
例5.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习3.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A、B、C、D四点,试判定图形ABCD的形状.
直角梯形
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习3.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A、B、C、D四点,试判定图形ABCD的形状.
直角梯形
题型点拨——用斜率关系判断直线的位置关系或形状
先画图预判
再用斜率验证
练习4.已知矩形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),则第四个顶点D的坐标为________.
练习5.已知点A(0,3),B(-1,0),C(3,0),且四边形ABCD为直角梯形,求点D的坐标.
题型点拨——用斜率关系判断直线的位置关系或形状
析:kAB=3,kBC=0
则kAB·kBC=0≠-1,即AB与BC不垂直
①由AD//BC,BC⊥CD求D
②由AB//DC,AB⊥AD求D
分类讨论思想
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
【小结】与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
与斜率有关的最值或范围问题
