2.4 线段、角的轴对称性(1)课件(共36张PPT)苏科版数学八年级上册
文档属性
| 名称 | 2.4 线段、角的轴对称性(1)课件(共36张PPT)苏科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览








文档简介
(共36张PPT)
2 . 4
线段、角的轴对称性
回顾旧知
线段是轴对称图形吗?它的对称轴是什么?
什么叫线段的垂直平分线?
知识点 1
线段的垂直平分线的性质
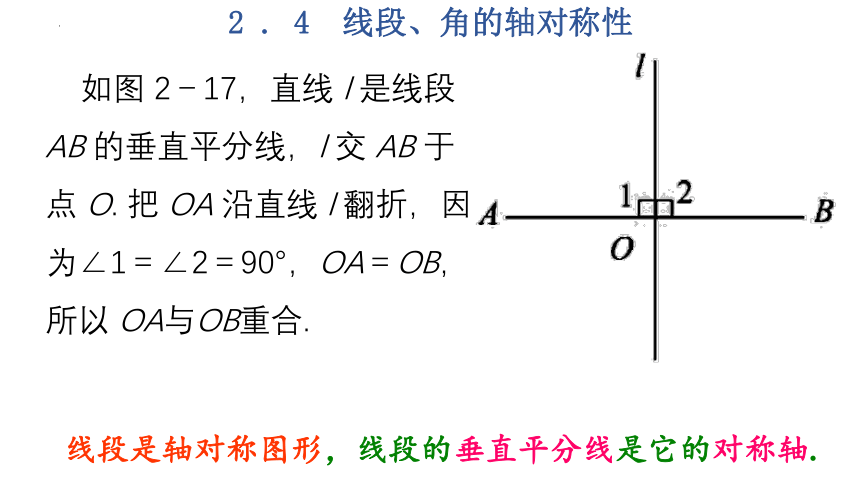
如图 2-17,直线 l 是线段AB 的垂直平分线,l 交 AB 于点 O. 把 OA 沿直线 l 翻折,因为∠1=∠2=90°,OA=OB,所以 OA与OB重合.
线段是轴对称图形,线段的垂直平分线是它的对称轴.
思 考
如图2-18,线段 AB 的垂直平分线 l 交 AB 于点O,点P在上 PA 与 PB 相等吗
我们可以运用图形运动的方法,利用线段的轴对称性,证明 PA=PB .
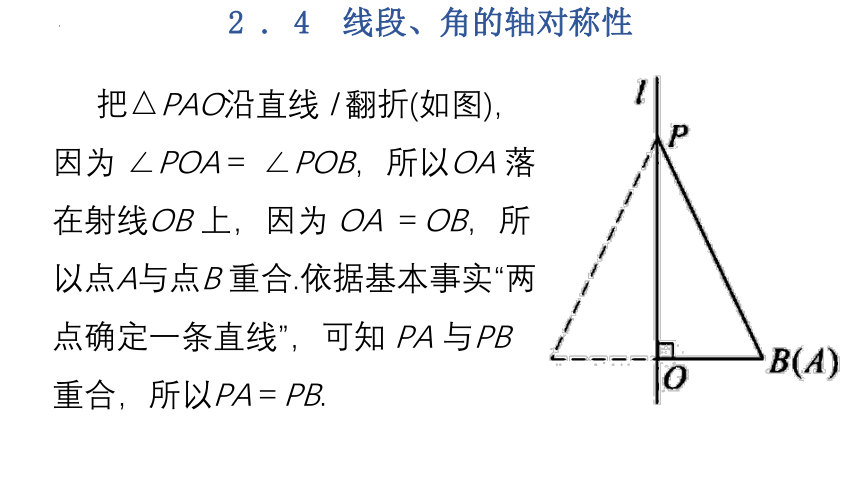
把△PAO沿直线 l 翻折(如图),因为 ∠POA= ∠POB,所以OA 落在射线OB 上,因为 OA =OB,所以点A与点B 重合.依据基本事实“两点确定一条直线”,可知 PA 与PB 重合,所以PA=PB.
于是,我们得到如下定理:
线段垂直平分线上的点到线段两端的距离相等.
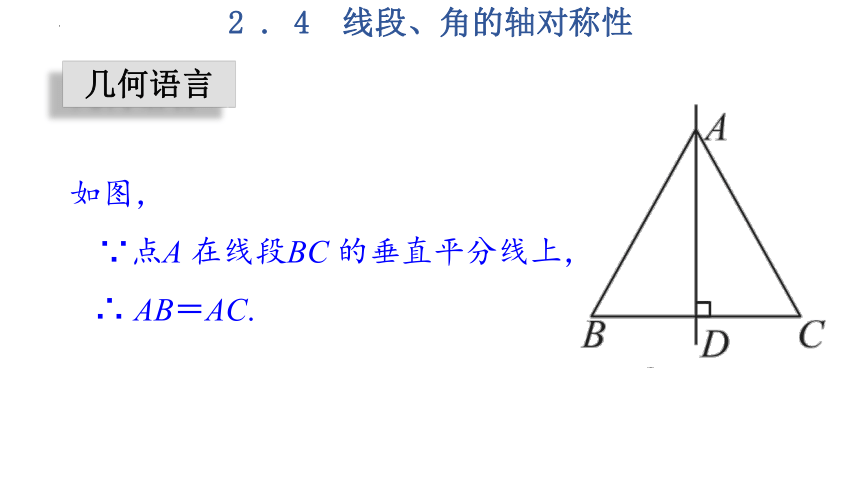
如图,
∵点A 在线段BC 的垂直平分线上,
∴ AB=AC.
几何语言
线段有两条对称轴,线段的垂直平分线是它的对称轴,线段自身所在的直线也是它的对称轴.
易错提醒
特别解读
1. 线段的垂直平分线的性质中的“距离”是“该点与这条线段两个端点的距离”.
2. 用线段的垂直平分线的性质可直接证明线段相等,不必再用三角形全等来证明,因此它为证明线段相等提供了新方法.
线段的垂直平分线外的点到这条线段两端的距离相等吗 为什么
讨 论
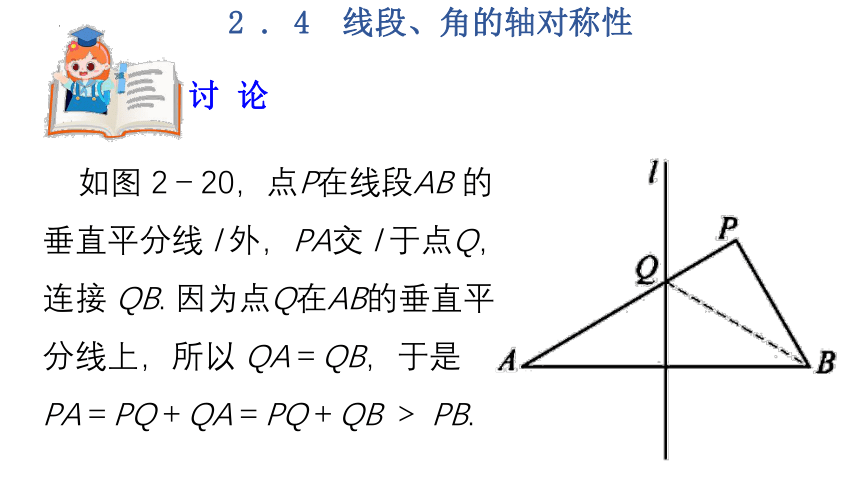
如图 2-20,点P在线段AB 的垂直平分线 l 外,PA交 l 于点Q,连接 QB. 因为点Q在AB的垂直平分线上,所以 QA=QB,于是 PA=PQ+QA=PQ+QB > PB.
练1
如图,在△ABC 中,AB 的垂直平分线分别交 AB、BC 于点D、E,连接AE. 若 AE=4,EC=2,则BC 的长是
( )
A. 2 B. 4
C. 6 D. 8
C
方法点拨
利用线段垂直平分线的性质进行线段间的转化,是一种常用的解题方法. 本题中解题的关键是利用线段垂直平分线的性质将BC 的长转化为线段
AE+EC 的长,即可求解.
解:∵直线DE 是AB 的垂直平分线,
∴ BE=AE.
∴ BC=BE+EC
=AE+EC
=4+2
=6.
练 习
1. 利用网格画线段 PQ 的垂直平分线 :
l
解:如图所示.
2. 如图,要在公路旁设一个公共汽车站,车站应设在什
么地方,才能使 A、B 两村到车站的距离相等
解:如图所示,连接 AB,作线段 AB 的垂直平分线l,直线l交公路于点 C,则点C就是汽车站的位置,此时 A,B 两村到车站的距离相等.
知识点 2
线段的垂直平分线的判定
思 考
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段两端的距离相等.反过来,如果一个点到一条线段两端的距离相等,那么这个点在这条线段的垂直平分线上吗
若点Q在线段 AB 上,且 QA =QB,则Q是线段 AB 的中点,点Q在线段AB的垂直平分线上(如图 2-21(1)).
若点Q在线段 AB 外,且 QA=QB,则作 QM⊥AB,垂足为 M (如图 2-21(2)).
由∠QMA=∠QMB=90°,QA=QB,QM=QM,可证 Rt△QAM ≌ Rt△QBM (HL).
由此可知AM=BM,即点Q在线
段AB的垂直平分线上.
于是,我们得到如下定理:
到线段两端距离相等的点在线段的垂直平分线上.
线段的垂直平分线是到线段两端距离相等的点的集合.
几何语言
如图,
∵ AB=AC,
∴点A 在线段BC 的垂直平分线上.
按下列作法,用直尺和圆规作线段 AB 的垂直平分线:
操 作
作 法 图 形
1.分别以点 A、B 为圆心,大于 AB 的长 为半径画弧,两弧相交于点 C、D. 2.过 C、D 两点作直线. 直线 CD 就是线段 AB 的垂直平分线.
交 流
在△ABC 中,用直尺和圆规分别作AB、AC的垂直平分线l1、l2,l1、l2 相交于点 O,再作 BC 的垂直平分线, 你有什么发现
BC 的垂直平分线过点O.
特别提醒
证明一个点在一条线段的垂直平分线上,还可以利用线段垂直平分线的定义进行推理,思路有两种:
一是作垂直,证平分;
二是取中点,证垂直.
例1 已知:如图2-22,在三△ABC中,AB、AC 的垂直
平分线 l1、l2 相交于点 O.
求证:点 O 在 BC 的垂直平分线上.
证明:连接 OA、OB、OC.
∵点O在AB 的垂直平分线l1 上,
∴ OA=OB
(线段垂直平分线上的点
到线段两端的距离相等).
同理 OA=OC.
∴OB=OC.
∴点 O 在 BC 的垂直平分线上
(到线段两端距离相等的点
在线段的垂直平分线上).
练2
如图,AD 为∠BAC 的平分线,交BC 于点D,AE=AF. 请判断线段AD 所在的直线是否为线段EF 的垂直平分线,若是,请给予证明;若不是,请说明理由.
教你一招
判断线段垂直平分线的两种方法:
一是定义法,二是判定定理.
一般习惯用定义法进行判断,而利用判定定理判断更简单. 用判定定理判定一条直线是线段的垂直平分线时,一定要证明直线上有两个不同的点到线段两个端点的距离相等.
解:线段AD 所在的直线是线段EF 的垂直平分线.
证明如下:连接DE、DF.
∵ AD 为∠BAC 的平分线,
∴∠EAD=∠FAD.
在△AED 和△ AFD 中,
AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△ AED ≌△ AFD.
∴ DE=DF.
∴点D 在线段EF 的垂直平分线上.
∵ AE=AF,
∴点A 在线段EF 的垂直平分线上.
∴线段AD 所在的直线是线段EF 的垂直平分线.
切忌只证明一个点在直线上,就说过该点的直线是线段的垂直平分线.
练 习
1. 利用网格在图中找一点 O,使OA=OB=OC.
O
2. 直线l 外有点 A、B,若要在 l 上找一点,使这点与点
A、B 的距离相等,这样的点一定能找到吗 请你画图
表示各种可能的情况.
解:不一定能找到,各种可能情况如图所示.
2 . 4
线段、角的轴对称性
回顾旧知
线段是轴对称图形吗?它的对称轴是什么?
什么叫线段的垂直平分线?
知识点 1
线段的垂直平分线的性质
如图 2-17,直线 l 是线段AB 的垂直平分线,l 交 AB 于点 O. 把 OA 沿直线 l 翻折,因为∠1=∠2=90°,OA=OB,所以 OA与OB重合.
线段是轴对称图形,线段的垂直平分线是它的对称轴.
思 考
如图2-18,线段 AB 的垂直平分线 l 交 AB 于点O,点P在上 PA 与 PB 相等吗
我们可以运用图形运动的方法,利用线段的轴对称性,证明 PA=PB .
把△PAO沿直线 l 翻折(如图),因为 ∠POA= ∠POB,所以OA 落在射线OB 上,因为 OA =OB,所以点A与点B 重合.依据基本事实“两点确定一条直线”,可知 PA 与PB 重合,所以PA=PB.
于是,我们得到如下定理:
线段垂直平分线上的点到线段两端的距离相等.
如图,
∵点A 在线段BC 的垂直平分线上,
∴ AB=AC.
几何语言
线段有两条对称轴,线段的垂直平分线是它的对称轴,线段自身所在的直线也是它的对称轴.
易错提醒
特别解读
1. 线段的垂直平分线的性质中的“距离”是“该点与这条线段两个端点的距离”.
2. 用线段的垂直平分线的性质可直接证明线段相等,不必再用三角形全等来证明,因此它为证明线段相等提供了新方法.
线段的垂直平分线外的点到这条线段两端的距离相等吗 为什么
讨 论
如图 2-20,点P在线段AB 的垂直平分线 l 外,PA交 l 于点Q,连接 QB. 因为点Q在AB的垂直平分线上,所以 QA=QB,于是 PA=PQ+QA=PQ+QB > PB.
练1
如图,在△ABC 中,AB 的垂直平分线分别交 AB、BC 于点D、E,连接AE. 若 AE=4,EC=2,则BC 的长是
( )
A. 2 B. 4
C. 6 D. 8
C
方法点拨
利用线段垂直平分线的性质进行线段间的转化,是一种常用的解题方法. 本题中解题的关键是利用线段垂直平分线的性质将BC 的长转化为线段
AE+EC 的长,即可求解.
解:∵直线DE 是AB 的垂直平分线,
∴ BE=AE.
∴ BC=BE+EC
=AE+EC
=4+2
=6.
练 习
1. 利用网格画线段 PQ 的垂直平分线 :
l
解:如图所示.
2. 如图,要在公路旁设一个公共汽车站,车站应设在什
么地方,才能使 A、B 两村到车站的距离相等
解:如图所示,连接 AB,作线段 AB 的垂直平分线l,直线l交公路于点 C,则点C就是汽车站的位置,此时 A,B 两村到车站的距离相等.
知识点 2
线段的垂直平分线的判定
思 考
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段两端的距离相等.反过来,如果一个点到一条线段两端的距离相等,那么这个点在这条线段的垂直平分线上吗
若点Q在线段 AB 上,且 QA =QB,则Q是线段 AB 的中点,点Q在线段AB的垂直平分线上(如图 2-21(1)).
若点Q在线段 AB 外,且 QA=QB,则作 QM⊥AB,垂足为 M (如图 2-21(2)).
由∠QMA=∠QMB=90°,QA=QB,QM=QM,可证 Rt△QAM ≌ Rt△QBM (HL).
由此可知AM=BM,即点Q在线
段AB的垂直平分线上.
于是,我们得到如下定理:
到线段两端距离相等的点在线段的垂直平分线上.
线段的垂直平分线是到线段两端距离相等的点的集合.
几何语言
如图,
∵ AB=AC,
∴点A 在线段BC 的垂直平分线上.
按下列作法,用直尺和圆规作线段 AB 的垂直平分线:
操 作
作 法 图 形
1.分别以点 A、B 为圆心,大于 AB 的长 为半径画弧,两弧相交于点 C、D. 2.过 C、D 两点作直线. 直线 CD 就是线段 AB 的垂直平分线.
交 流
在△ABC 中,用直尺和圆规分别作AB、AC的垂直平分线l1、l2,l1、l2 相交于点 O,再作 BC 的垂直平分线, 你有什么发现
BC 的垂直平分线过点O.
特别提醒
证明一个点在一条线段的垂直平分线上,还可以利用线段垂直平分线的定义进行推理,思路有两种:
一是作垂直,证平分;
二是取中点,证垂直.
例1 已知:如图2-22,在三△ABC中,AB、AC 的垂直
平分线 l1、l2 相交于点 O.
求证:点 O 在 BC 的垂直平分线上.
证明:连接 OA、OB、OC.
∵点O在AB 的垂直平分线l1 上,
∴ OA=OB
(线段垂直平分线上的点
到线段两端的距离相等).
同理 OA=OC.
∴OB=OC.
∴点 O 在 BC 的垂直平分线上
(到线段两端距离相等的点
在线段的垂直平分线上).
练2
如图,AD 为∠BAC 的平分线,交BC 于点D,AE=AF. 请判断线段AD 所在的直线是否为线段EF 的垂直平分线,若是,请给予证明;若不是,请说明理由.
教你一招
判断线段垂直平分线的两种方法:
一是定义法,二是判定定理.
一般习惯用定义法进行判断,而利用判定定理判断更简单. 用判定定理判定一条直线是线段的垂直平分线时,一定要证明直线上有两个不同的点到线段两个端点的距离相等.
解:线段AD 所在的直线是线段EF 的垂直平分线.
证明如下:连接DE、DF.
∵ AD 为∠BAC 的平分线,
∴∠EAD=∠FAD.
在△AED 和△ AFD 中,
AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△ AED ≌△ AFD.
∴ DE=DF.
∴点D 在线段EF 的垂直平分线上.
∵ AE=AF,
∴点A 在线段EF 的垂直平分线上.
∴线段AD 所在的直线是线段EF 的垂直平分线.
切忌只证明一个点在直线上,就说过该点的直线是线段的垂直平分线.
练 习
1. 利用网格在图中找一点 O,使OA=OB=OC.
O
2. 直线l 外有点 A、B,若要在 l 上找一点,使这点与点
A、B 的距离相等,这样的点一定能找到吗 请你画图
表示各种可能的情况.
解:不一定能找到,各种可能情况如图所示.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
