2023-2024学年苏科版数学八年级上册2.5 等腰三角形的轴对称性 第1课时 课件(共28张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册2.5 等腰三角形的轴对称性 第1课时 课件(共28张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 50.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
课时导入
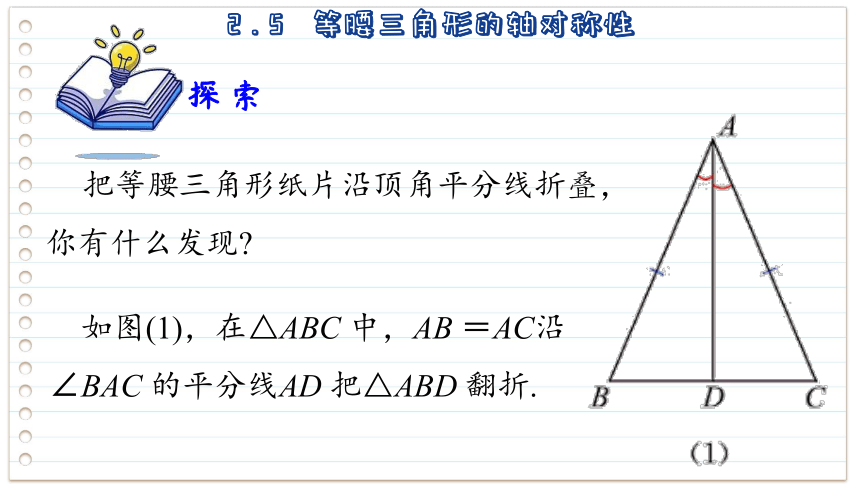
看到下边三角形了吗,它有何特点呢?
我们今天来探讨一下等腰三角形的性质.
腰
腰
顶角
底角
底角
底边
2 . 5
等腰三角形的轴对称性
第1课时
等腰三角形的性质
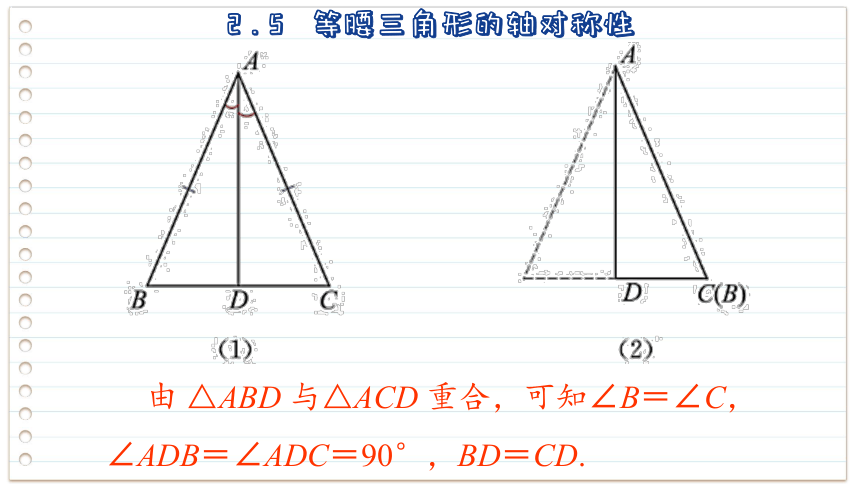
把等腰三角形纸片沿顶角平分线折叠,你有什么发现
如图(1),在△ABC 中,AB =AC沿∠BAC 的平分线AD 把△ABD 翻折.
探 索
因为∠BAD=∠CAD,
所以AB 落在射线 AC 上.
因为AB=AC,
所以点 B 与点 C 重合,
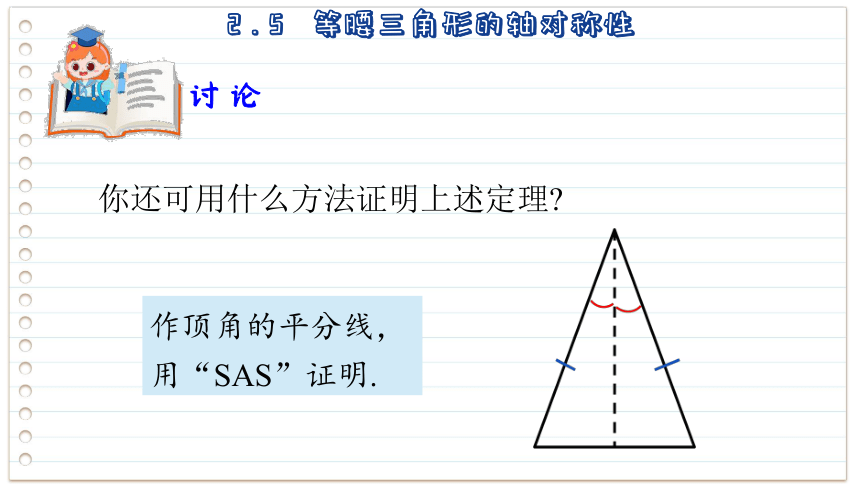
从而△ABD 与△ACD 重合(2).
等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴.
由 △ABD 与△ACD 重合,可知∠B=∠C,∠ADB=∠ADC=90°,BD=CD.
于是,我们得到如下定理:
等腰三角形的两底角相等(简称“等边对等角”).
等腰三角形底边上的高线、中线及顶角平分线重合.
讨 论
你还可用什么方法证明上述定理
作顶角的平分线,用“SAS”证明.
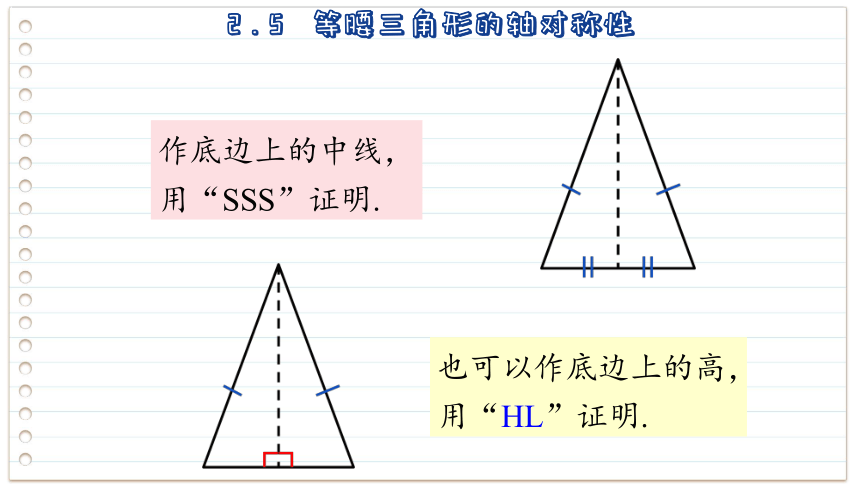
作底边上的中线,用“SSS”证明.
也可以作底边上的高,用“HL”证明.
几何语言:
如图,在△ ABC 中,
∵ AB=AC,
∴∠B =∠ C.
性质1
等腰三角形的两底角相等 (简称“等边对等角”).
作用:是证明角相等的常用方法,应用它证角相等时可省去三角形全等的证明,因而更简便.
特别提醒
性质2
等腰三角形底边上的高线、中线及顶角平分线重合
(简称“三线合一”).
(1) ∵ AB=AC,AD⊥BC,
∴ AD 平分∠ BAC,BD=DC.
(2)∵ AB=AC,BD=DC,
∴ AD⊥BC,AD 平分∠BAC.
(3)∵ AB=AC,AD 平分∠BAC,
∴ BD=DC,AD ⊥ BC.
几何语言:
练习
如图, 在△ABC 中,AB=AC,AD 平分∠BAC.
(1) 求∠ADB 的度数;
(2) 若∠BAC=100°,求∠B、∠C 的度数;
(3) 若BC=3 cm,求BD 的长.
(1) 在等腰三角形中,运用“三线合一”时,已知其中“一线”,就可以得到另外“两线”. 根据等腰三角形的“三线合一”的性质可以得到等线段、等角以及两条线段互相垂直.
(2) “等边对等角”的前提是在同一个三角形中.
特别提醒
(1) 求∠ADB 的度数;
解:∵ AB=AC,AD平分∠BAC,
∴ AD ⊥ BC,
∴∠ ADB=90° .
(2) 若∠BAC=100°,求∠B、∠C 的度数;
解:在△ABC 中,
∵ AB=AC,∠BAC=100°,
∴ ∠B =∠C=×(180 °- ∠BAC)
= ×(180 °-100°)
= 40°.
(3) 若BC=3 cm,求BD 的长.
解:∵ AB=AC,AD 平分∠BAC,
∴ AD 是BC 边上的中线,
∴ BD= BC= ×3=1.5(cm),
即BD 的长是1.5 cm.
操 作
按下列作法,用直尺和圆规作等腰三角形 ABC,使底边 BC=a,高AD=h.
作 法 图 形
1. 作线段 BC=a. 2. 作线段 BC的垂直平分线MN,MN交BC 于点 D. 3. 在 MN 上截取线段 DA,使 DA=h. 4. 连接 AB、AC. △ABC 就是所求作的等腰三角形.
例 1 已知:如图2-30,在△ABC 中,AB=AC,点D
在BC 上,目AD=BD.
求证:∠ADB=∠BAC.
思考与表述
要证 ∠ADB=∠BAC,
由于 ∠BAC=∠1+∠2,
∠ADB=∠C+∠2.
只要证 ∠1=∠C.
只要找与∠1相等且与∠C也相等的角.
怎么想 怎么写
证明:
∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB 是△ADC 的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
练 习
1. 在 △ABC 中,AB=AC,点D在 BC 上.
如果∠BAD =∠CAD,那么AD⊥BC,BD=CD;
如果 BD=CD,那么∠_______=∠_______,________⊥________;
如果 AD⊥BC,那么________________,________.
BAD
CAD
AD
BC
∠BAD=∠CAD
BD=CD
2. 在 △ABC 中,AB=AC.
(1) 如果∠B=70°,那么∠C=_______°,
∠A=_______°;
(2) 如果∠A=70°,那么∠B= _______°,
∠C=_______°;
(3) 如果有一个角等于120°,那么∠A= _______°,
∠B =_______°,∠C = _______°.
70
40
55
55
120
30
30
(4) 如果有一个角等于 50°,那么另两个角等于多少度
解:当顶角为 50°,即∠A = 50°时,另两个角∠B=∠C =(180° - 50°) ÷2 = 65°;
当底角为 50°,如∠B=50°时,则另两个角∠C=50°,∠A=180° - 50° × 2 = 80°.
3. 在如图的房屋人字梁架中,AB=AC,∠BAC = 110°,
AD⊥BC.
求∠B、∠C、∠BAD、∠CAD 的度数.
解:∵AB = AC,∠BAC = 110°,
∴ ∠B=∠C ==35°(等边对等角).
又∵AD⊥BC,
∴AD 平分∠BAC(等腰三角形底边上的高线、顶角平分线重合),
即∠BAD=∠CAD=∠BAC=55°.
本课结束
This lesson is over
THANKS!
课时导入
看到下边三角形了吗,它有何特点呢?
我们今天来探讨一下等腰三角形的性质.
腰
腰
顶角
底角
底角
底边
2 . 5
等腰三角形的轴对称性
第1课时
等腰三角形的性质
把等腰三角形纸片沿顶角平分线折叠,你有什么发现
如图(1),在△ABC 中,AB =AC沿∠BAC 的平分线AD 把△ABD 翻折.
探 索
因为∠BAD=∠CAD,
所以AB 落在射线 AC 上.
因为AB=AC,
所以点 B 与点 C 重合,
从而△ABD 与△ACD 重合(2).
等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴.
由 △ABD 与△ACD 重合,可知∠B=∠C,∠ADB=∠ADC=90°,BD=CD.
于是,我们得到如下定理:
等腰三角形的两底角相等(简称“等边对等角”).
等腰三角形底边上的高线、中线及顶角平分线重合.
讨 论
你还可用什么方法证明上述定理
作顶角的平分线,用“SAS”证明.
作底边上的中线,用“SSS”证明.
也可以作底边上的高,用“HL”证明.
几何语言:
如图,在△ ABC 中,
∵ AB=AC,
∴∠B =∠ C.
性质1
等腰三角形的两底角相等 (简称“等边对等角”).
作用:是证明角相等的常用方法,应用它证角相等时可省去三角形全等的证明,因而更简便.
特别提醒
性质2
等腰三角形底边上的高线、中线及顶角平分线重合
(简称“三线合一”).
(1) ∵ AB=AC,AD⊥BC,
∴ AD 平分∠ BAC,BD=DC.
(2)∵ AB=AC,BD=DC,
∴ AD⊥BC,AD 平分∠BAC.
(3)∵ AB=AC,AD 平分∠BAC,
∴ BD=DC,AD ⊥ BC.
几何语言:
练习
如图, 在△ABC 中,AB=AC,AD 平分∠BAC.
(1) 求∠ADB 的度数;
(2) 若∠BAC=100°,求∠B、∠C 的度数;
(3) 若BC=3 cm,求BD 的长.
(1) 在等腰三角形中,运用“三线合一”时,已知其中“一线”,就可以得到另外“两线”. 根据等腰三角形的“三线合一”的性质可以得到等线段、等角以及两条线段互相垂直.
(2) “等边对等角”的前提是在同一个三角形中.
特别提醒
(1) 求∠ADB 的度数;
解:∵ AB=AC,AD平分∠BAC,
∴ AD ⊥ BC,
∴∠ ADB=90° .
(2) 若∠BAC=100°,求∠B、∠C 的度数;
解:在△ABC 中,
∵ AB=AC,∠BAC=100°,
∴ ∠B =∠C=×(180 °- ∠BAC)
= ×(180 °-100°)
= 40°.
(3) 若BC=3 cm,求BD 的长.
解:∵ AB=AC,AD 平分∠BAC,
∴ AD 是BC 边上的中线,
∴ BD= BC= ×3=1.5(cm),
即BD 的长是1.5 cm.
操 作
按下列作法,用直尺和圆规作等腰三角形 ABC,使底边 BC=a,高AD=h.
作 法 图 形
1. 作线段 BC=a. 2. 作线段 BC的垂直平分线MN,MN交BC 于点 D. 3. 在 MN 上截取线段 DA,使 DA=h. 4. 连接 AB、AC. △ABC 就是所求作的等腰三角形.
例 1 已知:如图2-30,在△ABC 中,AB=AC,点D
在BC 上,目AD=BD.
求证:∠ADB=∠BAC.
思考与表述
要证 ∠ADB=∠BAC,
由于 ∠BAC=∠1+∠2,
∠ADB=∠C+∠2.
只要证 ∠1=∠C.
只要找与∠1相等且与∠C也相等的角.
怎么想 怎么写
证明:
∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB 是△ADC 的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
练 习
1. 在 △ABC 中,AB=AC,点D在 BC 上.
如果∠BAD =∠CAD,那么AD⊥BC,BD=CD;
如果 BD=CD,那么∠_______=∠_______,________⊥________;
如果 AD⊥BC,那么________________,________.
BAD
CAD
AD
BC
∠BAD=∠CAD
BD=CD
2. 在 △ABC 中,AB=AC.
(1) 如果∠B=70°,那么∠C=_______°,
∠A=_______°;
(2) 如果∠A=70°,那么∠B= _______°,
∠C=_______°;
(3) 如果有一个角等于120°,那么∠A= _______°,
∠B =_______°,∠C = _______°.
70
40
55
55
120
30
30
(4) 如果有一个角等于 50°,那么另两个角等于多少度
解:当顶角为 50°,即∠A = 50°时,另两个角∠B=∠C =(180° - 50°) ÷2 = 65°;
当底角为 50°,如∠B=50°时,则另两个角∠C=50°,∠A=180° - 50° × 2 = 80°.
3. 在如图的房屋人字梁架中,AB=AC,∠BAC = 110°,
AD⊥BC.
求∠B、∠C、∠BAD、∠CAD 的度数.
解:∵AB = AC,∠BAC = 110°,
∴ ∠B=∠C ==35°(等边对等角).
又∵AD⊥BC,
∴AD 平分∠BAC(等腰三角形底边上的高线、顶角平分线重合),
即∠BAD=∠CAD=∠BAC=55°.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
