2023-2024学年苏科版数学八年级上册3.1 勾股能理 课件(共34张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册3.1 勾股能理 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 49.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 17:46:49 | ||
图片预览






文档简介
(共34张PPT)
3 . 1
勾股定理
课时导入
1955 年希腊发行了一枚纪念邮票,邮票上的图案是根据一个著名的数学定理设计的.
观察这枚邮票上的图案,数一数图案中 3个正方形内小方格的个数,你有哪此发现
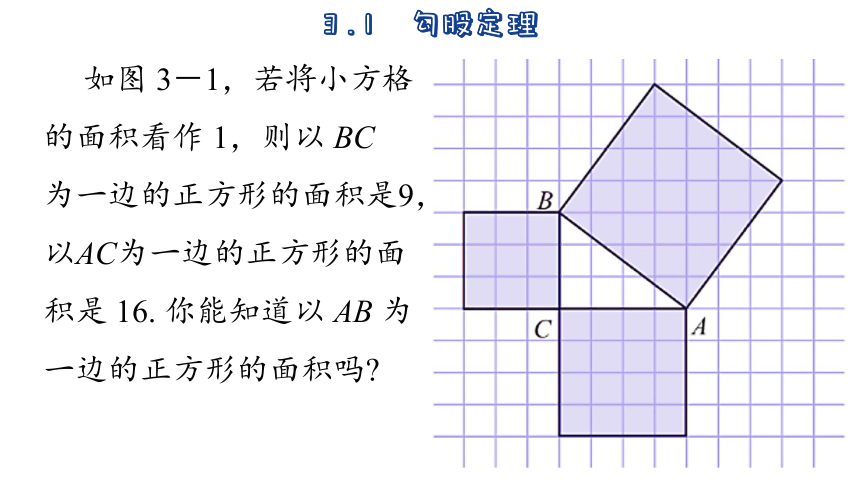
如图 3-1,若将小方格的面积看作 1,则以 BC 为一边的正方形的面积是9,以AC为一边的正方形的面积是 16. 你能知道以 AB 为一边的正方形的面积吗
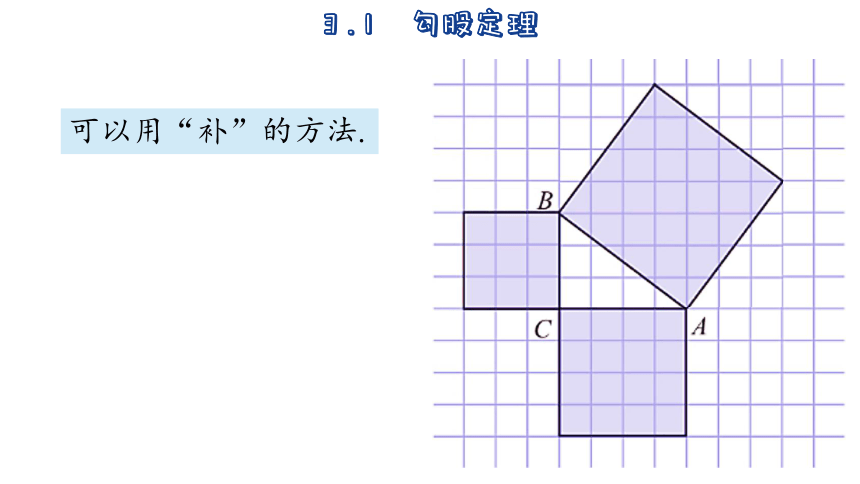
可以用“补”的方法.
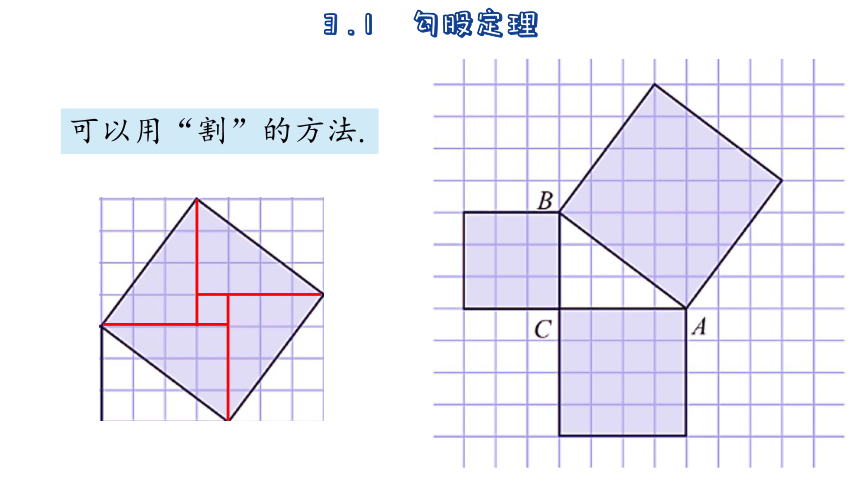
可以用“割”的方法.
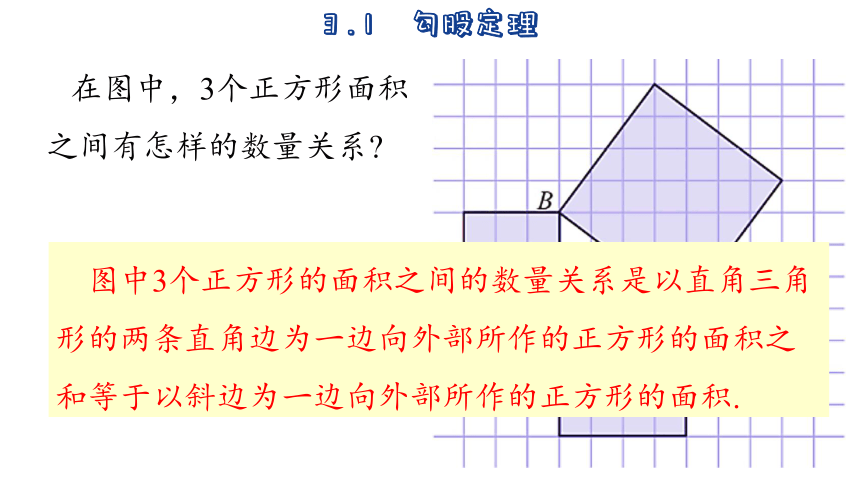
在图中,3个正方形面积之间有怎样的数量关系
图中3个正方形的面积之间的数量关系是以直角三角形的两条直角边为一边向外部所作的正方形的面积之和等于以斜边为一边向外部所作的正方形的面积.
操 作
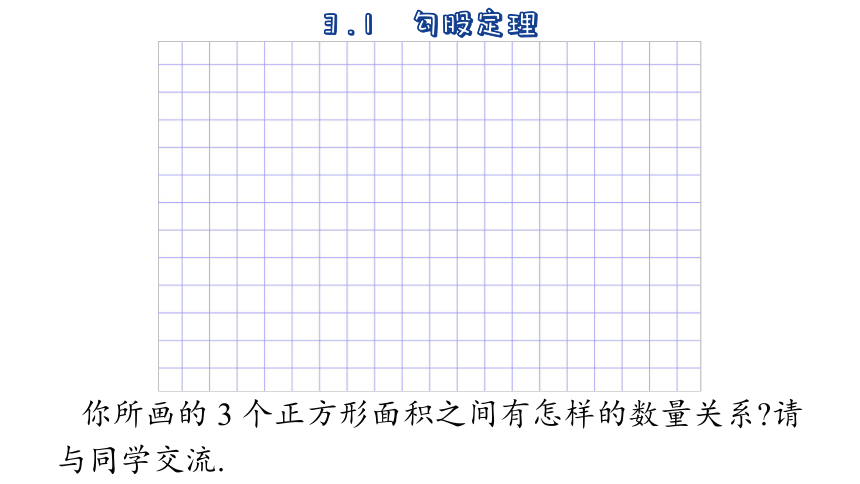
在下面的方格纸上,任意画一个顶点都在格点上的直角三角形并分别以这个直角三角形的各边为一边向三角形外部作正方形,仿照上面的方法计算以斜边为一边的正方形的面积.
你所画的 3 个正方形面积之间有怎样的数量关系 请与同学交流.
直角三角形的斜边、直角边有如下关系:
勾股定理 直角三角形两条直角边 a、b 的平方和等于斜边 c 的平方.
a2+b2=c2
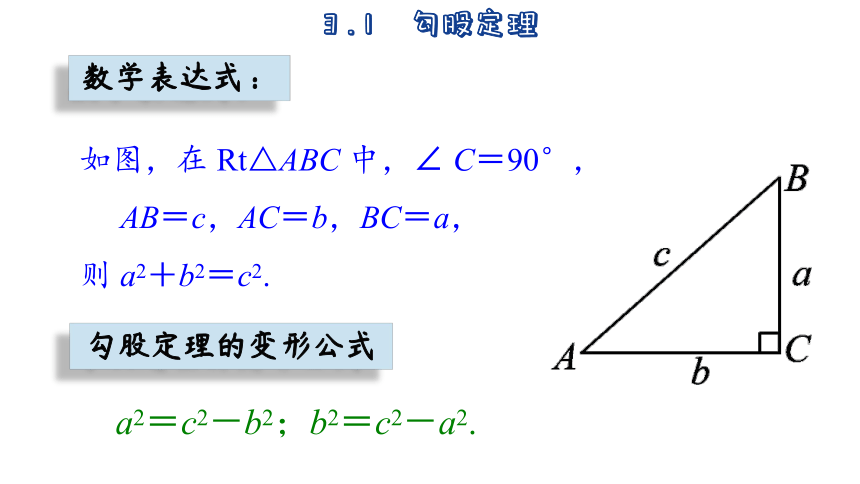
数学表达式:
如图,在 Rt△ABC 中,∠ C=90°,
AB=c,AC=b,BC=a,
则 a2+b2=c2.
勾股定理的变形公式
a2=c2-b2;b2=c2-a2.
我国古代把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 据《周算经》记载,公元前 1000 多年就发现了“勾三股四弦五”的结论.
练习
在Rt△ABC 中, ∠A,∠B,∠C 的对边分别为 a,b,c,∠C=90°.
(1) 已知 a=3,b=4,求c;
(2) 已知 c=17,a=8,求b;
(3) 已知 a∶b = 5∶12,c=13,求a 和b.
解法提醒
在一个直角三角形中:
1. 已知两条边长,若求斜边,则直接利用勾股定理的公式;若求直角边,则利用勾股定理的变形公式;
2. 已知一条边长以及另外两条边之间的数量关系,则需要设未知数表示另外两条边,然后根据勾股定理的公式列方程求解.
(1) 已知 a=3,b=4,求c;
解:∵∠C=90°,a=3,b=4,
∴由勾股定理,得
c2=a2+b2=32+42=25,
∴ c=5.
(2) 已知 c=17,a=8,求b;
解:∵∠C=90°,c=17,a=8,
∴由勾股定理,得
b2=c2-a2=172-82=225,
∴ b=15.
(3) 已知 a∶b = 5∶12,c=13,求a 和b.
解:∵ a∶b = 5∶12,
∴设a=5k,b=12k(k > 0),
∴ 由勾股定理,得(5k)2+ (12k)2=132,
解得 k=1 (k=-1 不符合题意,舍去),
∴ a=5,b=12.
练 习
1. 求下列直角三角形中未知边的长.
解:①由勾股定理,得x2=52+122=169,∴x=13.
②由勾股定理,得x2=172-82=225,∴x=15.
③由勾股定理,得x2=202-162=144,∴x=12.
2. 求下列图中 x、y、z 的值.
解:81+144=x2,
x2=225,
x=15.
解:y2+144=169,
y2=25,
y=5.
解:z2+576=625,
z2=49,
z=7.
3. 如图,△ABC 和△DEF 都不是直角三角形,分别以
△ABC和△DEF的各边为一边向三角形外部作正方形,
其中两个小正方形面积的和等于大正方形的面积吗
解:两个小正方形面积的和不等于大正方形的面积.
第一个图中△ABC 为锐角三角形,分别以 AC,BC,AB 为边的正方形的面积分别是 5,8,9,
∵5+8>9,
∴两个小正方形面积的和大于大正方形的面积;
第二个图中△DEF为钟角三角形,分别以 DE,EF,DF 为边的正方形的面积分别是 18,9,45,
∵18+9<45,
∴两个小正方形面积的和小于大正方形的面积.
事实上,以上结论对于所有的锐角三角形和钟角二角形都成立.
数学实验室
1. 制作 4 张如图 3-2 的直角三角形纸片.
2. 小明用这 4 张直角三角形纸片拼成图 3-3. 试用两种
不同的方法计算图 3-3的面积,你有什么发现
方法一:
图3-3的面积= (a+b)2;
方法二:
图3-3的面积=4×ab+c2.
由 (a+b)2 = 4× ab+c2 ,
可得 a2 + b2 = c2.
勾股定理得到验证.
3. 如图 3-4,把这 4 张纸片拼成一个边长为c的正方形,它的面积为 c2,你能用图3-4验证勾股定理吗
图3-4可以看成是由4个直角三角形与1个边长为(b-a)的小正方形组成的.它的面积为 4×ab+(b-a)2= a2+b2.
a2 + b2 = c2. 勾股定理得到验证.
公元3世纪,我国数学家赵爽曾用图 3-4 验证了勾股定理,这个图形被称为“弦图”.
2002 年国际数学家大会在北京召开,为弘扬我国古代数学文明.大会选用了“弦图”作为会标的中心图案 (如图 3-5).
探 索
把一个直立的火柴盒放倒. 你能用不同的方法计算梯形ABCD的面积,再次验证勾股定理吗
利用该图验证勾股定理方法如下:
如图,梯形 ABCD 的面积:
S梯形ABCD=(AB+CD) BC
= (a+b)(a+b)
= (a+b)2
S梯形ABCD = S△ABE+S△CDE+S△AED,
即(a+b)2 = ab+ ab+ c2
整理可得 a2+b2=c2
练 习
在 Rt△ABC中,∠C=90°.
(1) 如果 BC=9,AC=12,那么AB=________;
(2) 如果 BC=8,AB=10,那么AC=________;
(3) 如果 AB=13,AC=12,那么BC=________;
(4) 如果 AB=61,BC=11,那么AC=________.
15
6
5
60
本课结束
This lesson is over
THANKS!
3 . 1
勾股定理
课时导入
1955 年希腊发行了一枚纪念邮票,邮票上的图案是根据一个著名的数学定理设计的.
观察这枚邮票上的图案,数一数图案中 3个正方形内小方格的个数,你有哪此发现
如图 3-1,若将小方格的面积看作 1,则以 BC 为一边的正方形的面积是9,以AC为一边的正方形的面积是 16. 你能知道以 AB 为一边的正方形的面积吗
可以用“补”的方法.
可以用“割”的方法.
在图中,3个正方形面积之间有怎样的数量关系
图中3个正方形的面积之间的数量关系是以直角三角形的两条直角边为一边向外部所作的正方形的面积之和等于以斜边为一边向外部所作的正方形的面积.
操 作
在下面的方格纸上,任意画一个顶点都在格点上的直角三角形并分别以这个直角三角形的各边为一边向三角形外部作正方形,仿照上面的方法计算以斜边为一边的正方形的面积.
你所画的 3 个正方形面积之间有怎样的数量关系 请与同学交流.
直角三角形的斜边、直角边有如下关系:
勾股定理 直角三角形两条直角边 a、b 的平方和等于斜边 c 的平方.
a2+b2=c2
数学表达式:
如图,在 Rt△ABC 中,∠ C=90°,
AB=c,AC=b,BC=a,
则 a2+b2=c2.
勾股定理的变形公式
a2=c2-b2;b2=c2-a2.
我国古代把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 据《周算经》记载,公元前 1000 多年就发现了“勾三股四弦五”的结论.
练习
在Rt△ABC 中, ∠A,∠B,∠C 的对边分别为 a,b,c,∠C=90°.
(1) 已知 a=3,b=4,求c;
(2) 已知 c=17,a=8,求b;
(3) 已知 a∶b = 5∶12,c=13,求a 和b.
解法提醒
在一个直角三角形中:
1. 已知两条边长,若求斜边,则直接利用勾股定理的公式;若求直角边,则利用勾股定理的变形公式;
2. 已知一条边长以及另外两条边之间的数量关系,则需要设未知数表示另外两条边,然后根据勾股定理的公式列方程求解.
(1) 已知 a=3,b=4,求c;
解:∵∠C=90°,a=3,b=4,
∴由勾股定理,得
c2=a2+b2=32+42=25,
∴ c=5.
(2) 已知 c=17,a=8,求b;
解:∵∠C=90°,c=17,a=8,
∴由勾股定理,得
b2=c2-a2=172-82=225,
∴ b=15.
(3) 已知 a∶b = 5∶12,c=13,求a 和b.
解:∵ a∶b = 5∶12,
∴设a=5k,b=12k(k > 0),
∴ 由勾股定理,得(5k)2+ (12k)2=132,
解得 k=1 (k=-1 不符合题意,舍去),
∴ a=5,b=12.
练 习
1. 求下列直角三角形中未知边的长.
解:①由勾股定理,得x2=52+122=169,∴x=13.
②由勾股定理,得x2=172-82=225,∴x=15.
③由勾股定理,得x2=202-162=144,∴x=12.
2. 求下列图中 x、y、z 的值.
解:81+144=x2,
x2=225,
x=15.
解:y2+144=169,
y2=25,
y=5.
解:z2+576=625,
z2=49,
z=7.
3. 如图,△ABC 和△DEF 都不是直角三角形,分别以
△ABC和△DEF的各边为一边向三角形外部作正方形,
其中两个小正方形面积的和等于大正方形的面积吗
解:两个小正方形面积的和不等于大正方形的面积.
第一个图中△ABC 为锐角三角形,分别以 AC,BC,AB 为边的正方形的面积分别是 5,8,9,
∵5+8>9,
∴两个小正方形面积的和大于大正方形的面积;
第二个图中△DEF为钟角三角形,分别以 DE,EF,DF 为边的正方形的面积分别是 18,9,45,
∵18+9<45,
∴两个小正方形面积的和小于大正方形的面积.
事实上,以上结论对于所有的锐角三角形和钟角二角形都成立.
数学实验室
1. 制作 4 张如图 3-2 的直角三角形纸片.
2. 小明用这 4 张直角三角形纸片拼成图 3-3. 试用两种
不同的方法计算图 3-3的面积,你有什么发现
方法一:
图3-3的面积= (a+b)2;
方法二:
图3-3的面积=4×ab+c2.
由 (a+b)2 = 4× ab+c2 ,
可得 a2 + b2 = c2.
勾股定理得到验证.
3. 如图 3-4,把这 4 张纸片拼成一个边长为c的正方形,它的面积为 c2,你能用图3-4验证勾股定理吗
图3-4可以看成是由4个直角三角形与1个边长为(b-a)的小正方形组成的.它的面积为 4×ab+(b-a)2= a2+b2.
a2 + b2 = c2. 勾股定理得到验证.
公元3世纪,我国数学家赵爽曾用图 3-4 验证了勾股定理,这个图形被称为“弦图”.
2002 年国际数学家大会在北京召开,为弘扬我国古代数学文明.大会选用了“弦图”作为会标的中心图案 (如图 3-5).
探 索
把一个直立的火柴盒放倒. 你能用不同的方法计算梯形ABCD的面积,再次验证勾股定理吗
利用该图验证勾股定理方法如下:
如图,梯形 ABCD 的面积:
S梯形ABCD=(AB+CD) BC
= (a+b)(a+b)
= (a+b)2
S梯形ABCD = S△ABE+S△CDE+S△AED,
即(a+b)2 = ab+ ab+ c2
整理可得 a2+b2=c2
练 习
在 Rt△ABC中,∠C=90°.
(1) 如果 BC=9,AC=12,那么AB=________;
(2) 如果 BC=8,AB=10,那么AC=________;
(3) 如果 AB=13,AC=12,那么BC=________;
(4) 如果 AB=61,BC=11,那么AC=________.
15
6
5
60
本课结束
This lesson is over
THANKS!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
