2023-2024学年苏科版数学八年级上册4.1 平方根 课件(共38张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册4.1 平方根 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 52.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 17:56:06 | ||
图片预览









文档简介
(共38张PPT)
4 . 1
平方根
课时导入
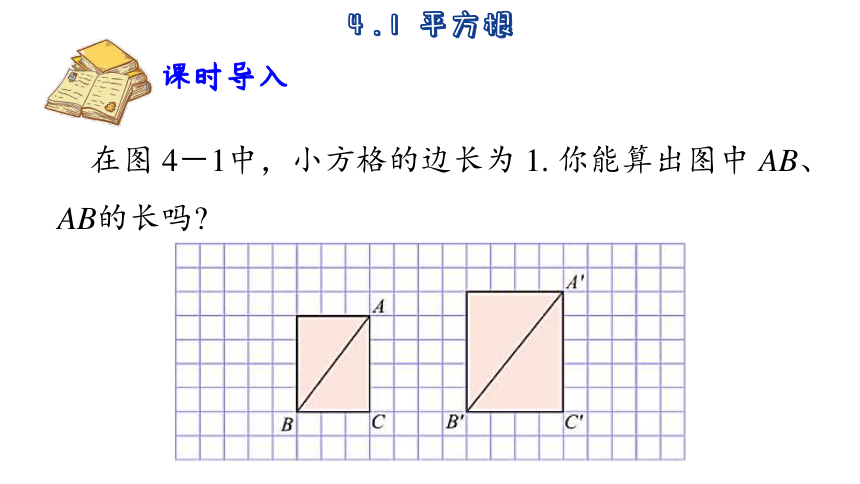
在图 4-1中,小方格的边长为 1. 你能算出图中 AB、AB的长吗
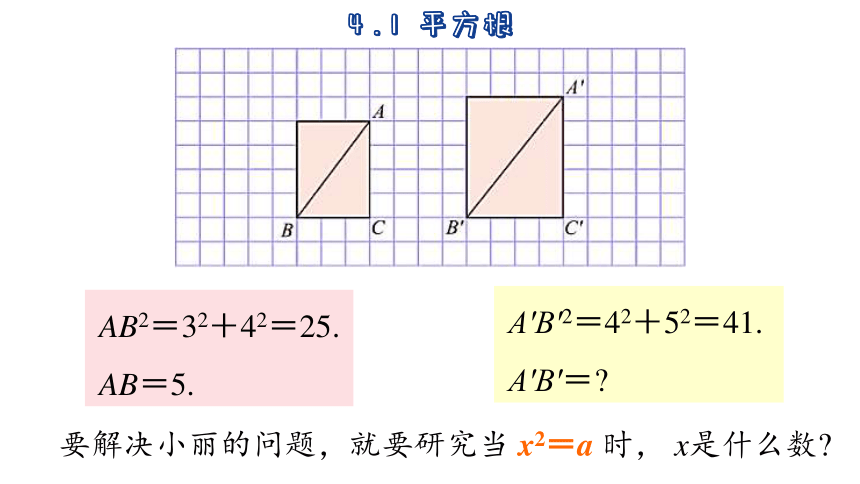
AB2=32+42=25.
AB=5.
A′B′2=42+52=41.
A′B′=
要解决小丽的问题,就要研究当 x2=a 时, x是什么数
当 x2=4 时,因为 22=4,(-2)2=4,所以 x=±2;
当 x2=100 时,因为 102=100,(-10)2=100,所以 x=±10;
当 x2=169 时,因为132=169,(-13)2=169,所以 x=±13.
可以看出,使 x2=a (a>0) 成立的数有两个,它们互为相反数.
如果 x2=a (a >0) 那么叫做 a 的平方根,也称为二次方根.
知识点 1 平方根
定 义
正数 a 的两个平方根记作± ,读作正、负根号a.
正数a 的正的平方根记作,
正数a 的负的平方根记作-.
表示方法
例如,2 的平方根记作± .
1. 求一个正数的平方根,先找出平方等于这个正数的数,这样的数有两个,它们互为相反数,因而这两个数均为这个正数的平方根.
2. (a≥0)实际上是省略了 2 中的2,2 叫做
根指数.
特别解读
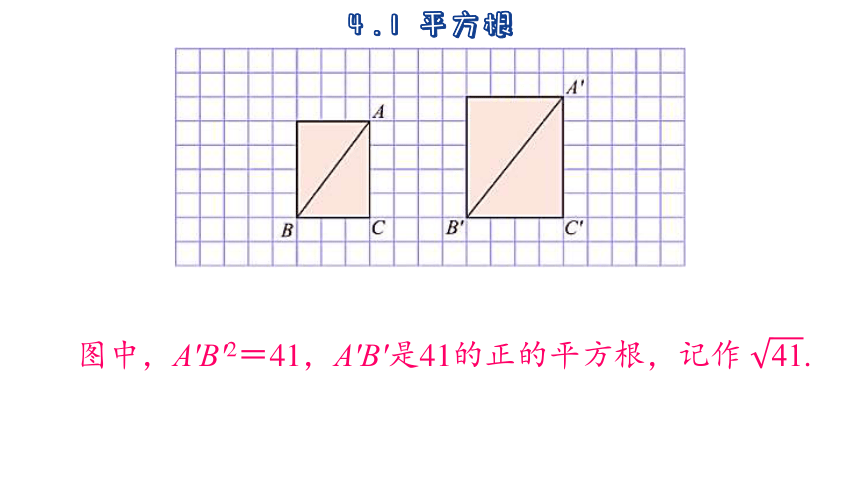
图中,A′B′2=41,A′B′是41的正的平方根,记作 .
我们曾将两个边长为 1 的正方形剪拼成一个边长为 a 的正方形,它的面积为 2,即 a2 = 2,a是2的正的平方根,记作 .
1
1
交 流
下列各数有平方根吗 如果有,请写出来;如果没有,请说明理由.
9,5,,0, -, -8,-36.
9,5,,0, -, -8,-36.
∵9>0,∴9有平方根,平方根是±.
∵5>0,∴5有平方根,平方根是±.
∵>0,∴ 有平方根,平方根是±.
0有平方根,0的平方根是0.
9,5,,0, -, -8,-36.
∵>0,∴- 没有平方根.
∵ -8<0,∴-8 没有平方根.
∵-36<0,∴-36 没有平方根.
一个正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
求一个数的平方根的运算叫做开平方.
例1 求下列各数的平方根:
(1) 25; (2) ; (3) 15; (4) 0.09.
解:(1) 25 的平方根是±,即±5;
(2) 的平方根是±,即±;
(3) 15 的平方根是± ;
(4) 0.09 的平方根是± ,即±0.3.
(1) 一个正数的平方根是2a-1 和a-5,则这个正数是多少?
练1
解:根据题意,得(2a-1) +(a-5)=0,
解得 a=2,
∴这个正数为(2a-1)2= (2×2-1)2=9.
(2) 已知2a-1 与-a+2 是 m 的平方根,求 m 的值.
解:根据题意,分以下两种情况:
① 当2a-1=-a+2 时,a=1,
∴ m= (2a-1)2= (2×1-1)2=1.
② 当(2a-1) +(-a+2) =0 时,a=-1,
∴ m= (2a-1)2=[2×(-1)-1]2= (-3)2=9.
故m 的值为1 或9.
练 习
写出下列各数的平方根:
81,289,0,2,2.56,0.81.
解:81的平方根是±,即±9;
289 的平方根是±,即±17;
0的平方根是0;
2= , 2的平方根是± ,即±;
2.56的平方根是±,即±1.6;
0.81的平方根是±,即±0.9.
知识点 2 算术平方根
定 义
我们知道,正数a有两个平方根±,我们把正数 a 的正的平方根,叫做 a 的算术平方根.
0 的平方根也叫做 0 的算术平方根,即 =0.
表示方法
正数a 的算术平方根表示为, 读作根号a,a 叫做被开方数.
例如,4 的平方根是±,即±2,其中2叫做4的算术平方根;
2 的平方根是±,其中叫做 2 的算术平方根.
(1) 算术平方根 具有双重非负性:
① 被开方数a 是非负数,即a ≥ 0;
② 算术平方根是非负数,即 ≥0.
(2) 算术平方根是它本身的数只有0 和1.
特别解读:
1. 区分清楚算术平方根是平方根中的一个;
2. 求一个正数的平方根时,不能遗漏负的平方根.
易错警示
例2 求下列各数的算术平方根:
(1) 625; (2) 0.008 1; (3) 7.
解:(1) 625 的算术平方根是,即 25;
(2) 0.0081的算术平方根是,即 0.09;
(3) 7 的算术平方根是 .
练2
求下列各数的算术平方根:
(1) 2 ; (2) (-5)2; (3) ; (4)7.
解:(1)因为 ()2 ==2,
所以 2 的算术平方根是 ,即 = .
(2) 因为(-5)2 = 52,
所以(-5)2 的算术平方根是5,即 (-5)2 = 5.
(3) 因为 = 9,9 的算术平方根是3,
所以 的算术平方根是3.
(4) 7 的算术平方根是 .
求一个数的算术平方根必须明确两点:
1. 这个数是非负数;
2 .求出的算术平方根(结果)必须是非负数.
知识储备
例3 ()2、()2、 有意义吗 如果有,求它的值.
解: ()2表示“3 的算术平方根的平方”,根据算术平方根的意义,得()2 = 3.
没有意义, ()2 也就没有意义.
表示-5 的平方 (即 25) 的算术平方根, =5.
例 4 “欲穷千里目,更上一层楼”. 说的是登得高看得远。如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则 d≈,其中 R 是地球半径,约等于6400 km.
小丽站在海边的一块岩石上,眼睛离海平面的高度h为 20 m,她观测到远处一艘船刚露出海平面,求此时d的值.
解:由 R=6400 km,h=0.02 km,
得 d≈
==16(km).
练3
已知直角三角形的两边长分别为3 和4,求第三边的长.
解:当两条直角边的长分别为3 和4 时,第三边的长为 = =5;
当斜边的长为4,一条直角边的长为3 时,第三边的长为 = .
思 考
1. ()2 等于多少 ()2 呢
()2=(0.1)2 = 0.01.
()2=5.
2. 等于多少 等于多少
=16.
=16.
练 习
1. 写出下列各数的算术平方根:
0.01, ,0,10, (-)2.
解:0.01的算术平方根是,即0.1;
的算术平方根是,即.
0 的算术平方根是0;
10 的算术平方根是;
(-)2的算术平方根是.
2. ()2、()2、、 有意义吗 如果有,
求它的值.
解: ()2、、 有意义,
()2 =4, = , =2.
()2无意义.
本课小结
平方根
1. 定义:
若x2=a,则x叫做a的平方根.
2. 性质:
一个正数有两个平方根,它们互为相反数,
0的平方根是0,负数没有平方根.
3. 平方根与开平方间的关系:
(1)开平方是求平方根的运算;
(2)平方根是开平方运算的结果.
4. 求一个非负数的平方根的方法:
① 求一个非负数a的平方根,就是要把平方后等于a的
数找出来,从而求出a的所有平方根;
② 求带分数的平方根时,应先将带分数化为假分数,
这也是常出错的地方.
注意:正数的平方根有两个,前面必定有“±”号.
4 . 1
平方根
课时导入
在图 4-1中,小方格的边长为 1. 你能算出图中 AB、AB的长吗
AB2=32+42=25.
AB=5.
A′B′2=42+52=41.
A′B′=
要解决小丽的问题,就要研究当 x2=a 时, x是什么数
当 x2=4 时,因为 22=4,(-2)2=4,所以 x=±2;
当 x2=100 时,因为 102=100,(-10)2=100,所以 x=±10;
当 x2=169 时,因为132=169,(-13)2=169,所以 x=±13.
可以看出,使 x2=a (a>0) 成立的数有两个,它们互为相反数.
如果 x2=a (a >0) 那么叫做 a 的平方根,也称为二次方根.
知识点 1 平方根
定 义
正数 a 的两个平方根记作± ,读作正、负根号a.
正数a 的正的平方根记作,
正数a 的负的平方根记作-.
表示方法
例如,2 的平方根记作± .
1. 求一个正数的平方根,先找出平方等于这个正数的数,这样的数有两个,它们互为相反数,因而这两个数均为这个正数的平方根.
2. (a≥0)实际上是省略了 2 中的2,2 叫做
根指数.
特别解读
图中,A′B′2=41,A′B′是41的正的平方根,记作 .
我们曾将两个边长为 1 的正方形剪拼成一个边长为 a 的正方形,它的面积为 2,即 a2 = 2,a是2的正的平方根,记作 .
1
1
交 流
下列各数有平方根吗 如果有,请写出来;如果没有,请说明理由.
9,5,,0, -, -8,-36.
9,5,,0, -, -8,-36.
∵9>0,∴9有平方根,平方根是±.
∵5>0,∴5有平方根,平方根是±.
∵>0,∴ 有平方根,平方根是±.
0有平方根,0的平方根是0.
9,5,,0, -, -8,-36.
∵>0,∴- 没有平方根.
∵ -8<0,∴-8 没有平方根.
∵-36<0,∴-36 没有平方根.
一个正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
求一个数的平方根的运算叫做开平方.
例1 求下列各数的平方根:
(1) 25; (2) ; (3) 15; (4) 0.09.
解:(1) 25 的平方根是±,即±5;
(2) 的平方根是±,即±;
(3) 15 的平方根是± ;
(4) 0.09 的平方根是± ,即±0.3.
(1) 一个正数的平方根是2a-1 和a-5,则这个正数是多少?
练1
解:根据题意,得(2a-1) +(a-5)=0,
解得 a=2,
∴这个正数为(2a-1)2= (2×2-1)2=9.
(2) 已知2a-1 与-a+2 是 m 的平方根,求 m 的值.
解:根据题意,分以下两种情况:
① 当2a-1=-a+2 时,a=1,
∴ m= (2a-1)2= (2×1-1)2=1.
② 当(2a-1) +(-a+2) =0 时,a=-1,
∴ m= (2a-1)2=[2×(-1)-1]2= (-3)2=9.
故m 的值为1 或9.
练 习
写出下列各数的平方根:
81,289,0,2,2.56,0.81.
解:81的平方根是±,即±9;
289 的平方根是±,即±17;
0的平方根是0;
2= , 2的平方根是± ,即±;
2.56的平方根是±,即±1.6;
0.81的平方根是±,即±0.9.
知识点 2 算术平方根
定 义
我们知道,正数a有两个平方根±,我们把正数 a 的正的平方根,叫做 a 的算术平方根.
0 的平方根也叫做 0 的算术平方根,即 =0.
表示方法
正数a 的算术平方根表示为, 读作根号a,a 叫做被开方数.
例如,4 的平方根是±,即±2,其中2叫做4的算术平方根;
2 的平方根是±,其中叫做 2 的算术平方根.
(1) 算术平方根 具有双重非负性:
① 被开方数a 是非负数,即a ≥ 0;
② 算术平方根是非负数,即 ≥0.
(2) 算术平方根是它本身的数只有0 和1.
特别解读:
1. 区分清楚算术平方根是平方根中的一个;
2. 求一个正数的平方根时,不能遗漏负的平方根.
易错警示
例2 求下列各数的算术平方根:
(1) 625; (2) 0.008 1; (3) 7.
解:(1) 625 的算术平方根是,即 25;
(2) 0.0081的算术平方根是,即 0.09;
(3) 7 的算术平方根是 .
练2
求下列各数的算术平方根:
(1) 2 ; (2) (-5)2; (3) ; (4)7.
解:(1)因为 ()2 ==2,
所以 2 的算术平方根是 ,即 = .
(2) 因为(-5)2 = 52,
所以(-5)2 的算术平方根是5,即 (-5)2 = 5.
(3) 因为 = 9,9 的算术平方根是3,
所以 的算术平方根是3.
(4) 7 的算术平方根是 .
求一个数的算术平方根必须明确两点:
1. 这个数是非负数;
2 .求出的算术平方根(结果)必须是非负数.
知识储备
例3 ()2、()2、 有意义吗 如果有,求它的值.
解: ()2表示“3 的算术平方根的平方”,根据算术平方根的意义,得()2 = 3.
没有意义, ()2 也就没有意义.
表示-5 的平方 (即 25) 的算术平方根, =5.
例 4 “欲穷千里目,更上一层楼”. 说的是登得高看得远。如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则 d≈,其中 R 是地球半径,约等于6400 km.
小丽站在海边的一块岩石上,眼睛离海平面的高度h为 20 m,她观测到远处一艘船刚露出海平面,求此时d的值.
解:由 R=6400 km,h=0.02 km,
得 d≈
==16(km).
练3
已知直角三角形的两边长分别为3 和4,求第三边的长.
解:当两条直角边的长分别为3 和4 时,第三边的长为 = =5;
当斜边的长为4,一条直角边的长为3 时,第三边的长为 = .
思 考
1. ()2 等于多少 ()2 呢
()2=(0.1)2 = 0.01.
()2=5.
2. 等于多少 等于多少
=16.
=16.
练 习
1. 写出下列各数的算术平方根:
0.01, ,0,10, (-)2.
解:0.01的算术平方根是,即0.1;
的算术平方根是,即.
0 的算术平方根是0;
10 的算术平方根是;
(-)2的算术平方根是.
2. ()2、()2、、 有意义吗 如果有,
求它的值.
解: ()2、、 有意义,
()2 =4, = , =2.
()2无意义.
本课小结
平方根
1. 定义:
若x2=a,则x叫做a的平方根.
2. 性质:
一个正数有两个平方根,它们互为相反数,
0的平方根是0,负数没有平方根.
3. 平方根与开平方间的关系:
(1)开平方是求平方根的运算;
(2)平方根是开平方运算的结果.
4. 求一个非负数的平方根的方法:
① 求一个非负数a的平方根,就是要把平方后等于a的
数找出来,从而求出a的所有平方根;
② 求带分数的平方根时,应先将带分数化为假分数,
这也是常出错的地方.
注意:正数的平方根有两个,前面必定有“±”号.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
