2023-2024学年苏科版数学八年级上册5.2 平面直角坐标系 第2课时 课件(共52张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册5.2 平面直角坐标系 第2课时 课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 17:59:42 | ||
图片预览








文档简介
(共52张PPT)
5 . 2
平面直角坐标系
第2课时
用坐标表示平移
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
1、平移的定义
回顾旧知
(2) 经过平移后,对应点所连的线段 平行且相等;
2、平移的性质
(1) 平移不改变图形的形状和大小,只改变形图
形的位置.
例3 如图,点B、点C在轴上,试在第一象限内画以BC 为底、面积为 10 的等腰三角形ABC,并写出点 A、点 B、点 C的坐标.
解:点 B、C的坐标分别为B(1,0)、C(5,0),BC=4.根据题意,可知等腰三角形 ABC的高为5,点A在 BC 的垂直平分线上,它的横坐标为 3,纵坐标为 5,即 A(3,5).所画ABC 如图.
A
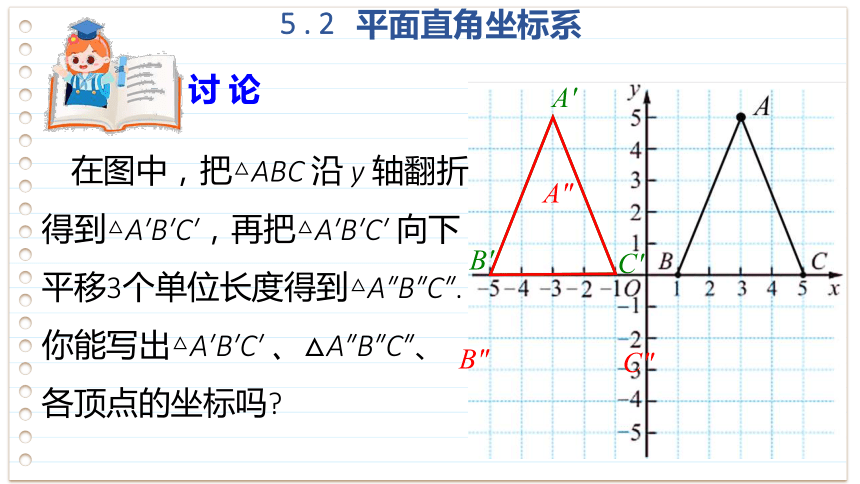
讨 论
在图中,把△ABC 沿 y 轴翻折得到△A′B′C′,再把△A′B′C′ 向下平移3个单位长度得到△A″B″C″. 你能写出△A′B′C′ 、△A″B″C″、各顶点的坐标吗
A′
B′
C′
A″
B″
C″
A′
B′
C′
A″
B″
C″
A′ (-3,5),
B′ (-1,0),
C′ (-5,0).
A″ (-3,2),
B″ (-1,-3),
C″ (-5,-3).
数学实验室
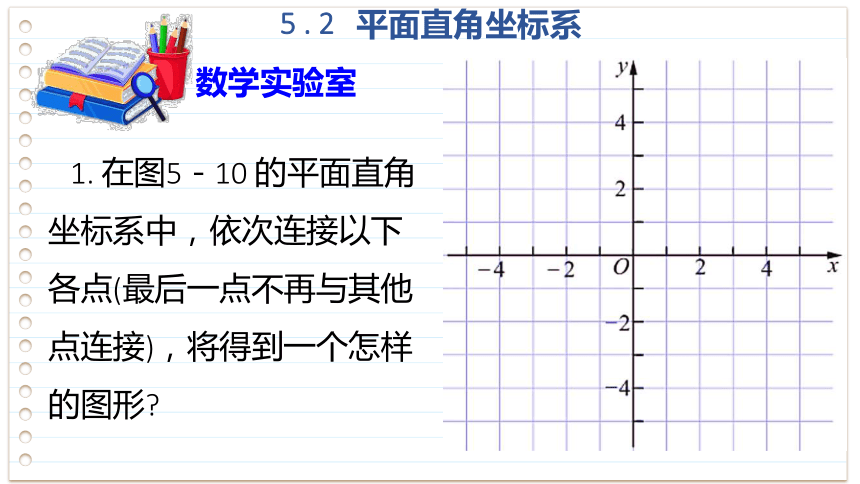
1. 在图5-10 的平面直角坐标系中,依次连接以下各点(最后一点不再与其他点连接),将得到一个怎样的图形
(0.5,4),(0,0),(1,3),
(2,3),(3,2),(3,0),
(1,-1),(2,-1),
(1,-3),(0,-1),
(-1,-3),(-2,-1),
(-1,-1),(-3,0),
(-3,2),(-2,3),
(-1,3),(0,0),(-0.5,4).
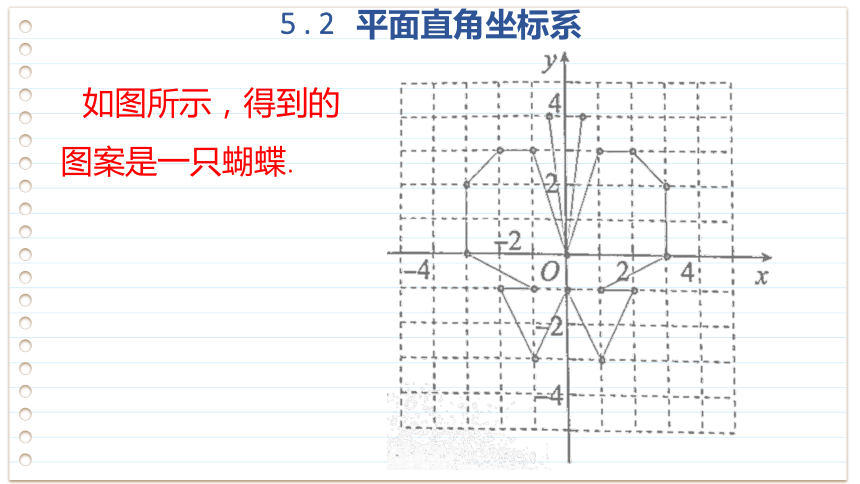
如图所示,得到的图案是一只蝴蝶.
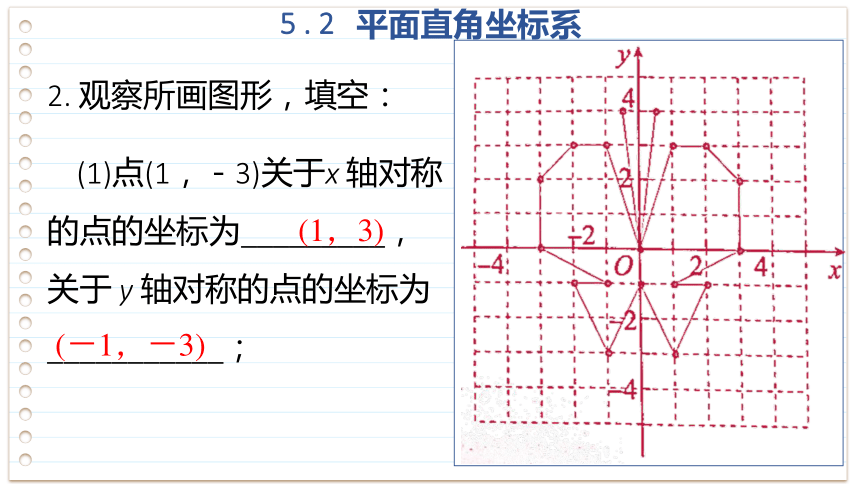
2. 观察所画图形,填空:
(1)点(1,-3)关于x 轴对称的点的坐标为_________,关于 y 轴对称的点的坐标为___________;
(1,3)
(-1,-3)
(2)点(-1,3)关于 x 轴对称的点的坐标为__________,关于 y 轴对称的点的坐标为___________.
一般地,点 P(a,b)关于x 轴对称的点的坐标为______,关于 y 轴对称的点的坐标为________.
(-1,-3)
(1,3)
(a,-b)
(-a,b)
3. 在图 5-11中,把线段 AB 先向右平移 7个单位长度,再向上平移 2个单位长度,得到线段 A′B′. 试分别写出点A、B、A′、B′的坐标.
A(-4,1),B(-2,3),
A′(3,3),B′(5,5).
A′
B′
(1) 你能说出点A与点A′、点 B与点 B′的坐标之间的关系吗
A′
B′
点A′的横坐标比点A的横坐标大7,点A′的纵坐标比点A的纵坐标大 2;点B′的横坐标比点B 的横坐标大 7,点B′的纵坐标比点B′的纵坐标大2.
(2) 如果点C(m,n)是线段AB 上的任意一点,那么当AB 平移到A′B′后,写出与点 C 对应的点C′的坐标.
A′
B′
C′ (m+7,n+2).
思 考
如果一个点的纵坐标不变,横坐标改变,那么这个点的位置发生怎样的变化 如果一个点的横坐标不变,纵坐标改变呢
如果一个点的纵坐标不变,横坐标改变,那么该点将向左或向右平移;如果一个点的横坐标不变,纵坐标改变,那么该点将向上或向下平移.
在平面直角坐标系中,点P(a,b)向右(或向左)平移n(n>0)个单位长度,则点P 的纵坐标不变,横坐标加上(或减去)n;
点P(a,b)向上(或向下)平移n(n>0)个单位长度,则点P 的横坐标不变,纵坐标加上(或减去)n.
规 律 总 结
点 P(a,b) 关于 x 轴对称的点的坐标为(a,-b),关于 y 轴对称的点的坐标为(-a,b),关于原点对称的点的坐标为(-a,-b).
将点P(a,b)绕原点旋转180°,得P′(-a,b).
平面内点P(a,b)到原点O 的距离OP=.
练 4
在平面直角坐标系中,点M 的坐标为(1,-3).如果把点M 先向左平移5 个单位长度,再向上平移3 个单位长度得到点M′,则M′的坐标为( )
A. (6,0) B. (6,- 6)
C. (- 4,0) D. (- 4,- 6)
C
练 5
如果点 P (-2,b)和点 Q (a,-3) 关于x 轴对称,则a+b 的值是( )
A. -1 B . 1
C . -5 D . 5
B
练 习
(1) 写出图①中点A、B、M、N
的坐标;
A (2,3),B (3,0),
M (1,1.5),N (2.5,1.5).
(2) 指出图①经过怎样的运动可以得到图②、图③、图④,并分别写出这3 个图中
与点 A、B、M、N 对应的
点A′、B′、M′、N′的坐标.
图②是由图①向右平移 2 个单位长度得到的;
图②中A′(4,3),B′(5,0),M′(3,1.5),N′(4.5,1.5)
图③是由图①沿x轴翻折得到的;
图中A′(2,-3),B′(3,0),M′(1,-1.5),N′(2.5,-1.5)
图④是由图①以点O为中心,顺时针旋转 90°得到的.
图④中A′(3,-2),B′(0,-3),M′(1.5,-1),N′(1.5,-2.5).
本课小结
用坐标表示平移
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
第3课时
用坐标表示地理位置
在茫茫的大海上,“北斗导航系统能对渔船进行准确定位. ”以便及时掌握各种情况.这个系统是怎样定位的呢,答案就在本节中.
思 考
如图 5-12,电视机厂通过由电脑控制的机械手,把各种元器件准确插入线路板上的焊孔,然后通过焊接工序将它们焊牢.
如果你是工程师,那么你怎样向机械手下达指令,使它把元器件准确插入相应的焊孔?
如果在线路板上建立平面直角坐标系,用坐标表示焊孔 A、B 的位置,那么向电脑输入点 A、B 的坐标后,机械手就会按坐标指示的“地址”将有关元器件准确插入焊孔 A、B.
例如,建立如图 5-13 的平面直角坐标系,则点 A 的坐标为(a,d),点B的坐标为(b,c).
(1) 选择一个适当的点为原点;
(2) 过原点在两个互相垂直的方向上分别作出
x 轴、y 轴;
(3) 根据具体问题确定单位长度.
建立平面直角坐标系的一般步骤
(1) 坐标轴的方向通常取水平方向为x轴,竖直方向为y轴;
(2)平面直角坐标系变化时,坐标平面内各点的坐标也发生变化,但各点之间的相对位置并不会发生变化.
特别解读
尝 试
在图5-14 中,以“中心广场”为坐标原点,以正东方向为 x 轴正方向、正北方向为 y 轴正方向,画出平面直角坐标系. 说出各旅游景点的位置 (小方格的边长为 1个长度单位).
画平面直角坐标系如图所示.
O(0,0),A(5,7),B(-8,5),C(-11,1),D(-8,-3),E(-12,-8),F(3,-6)
例4 已知正方形 ABCD 的边长为 4,建立适当的平面直角坐标系,分别写出各顶点的坐标.
解:如图 ,以点 A 为坐标原点,分别以边 AB、AD所在直线为x轴、y轴建立平面直角坐标系,点A的坐标为(0,0).
∵ AB=AD=4,
∴ 点B的坐标为(4,0),
点 D的坐标为(0,4).
∵ DC=AB,BC=AD,
∴ 点C的坐标为(4,4).
讨 论
还能建立不同的平面直角坐标系表示例4中正方形各顶点的坐标吗
根据实际问题的需要,建立恰当的平面直角坐标系,可以使一些点的坐标较为简明,便于研究和解决问题.
练 6
根据下面的条件画一幅示意图,并在图中标出各个景点的位置和坐标.
菊花园:从中心广场向北走150 m,再向东走150 m;
湖心亭:从中心广场向西走150 m,再向北走100 m;
松风亭:从中心广场向西走100 m,再向南走50 m;
育德泉:从中心广场向北走200 m.
练 习
1. 根据某动物园的平面示意图,以大门所在的位置为坐
标原点,以正东方向为x 轴正方向、正北方向为 y 轴
正方向,以l cm为单位长度,建立平面直角坐标系,
用坐标表示猴山、驼峰、百鸟园和熊猫馆的位置。
略
2. 在△PAB 中,PA=PB,AB=2. 建立适当的平面直角
坐标系,分别写出△PAB 是等边三角形、等腰直角三
角形时各顶点的坐标.
解:(1)当△PAB 是等边三角形时,建立如图1所示的平面直角坐标系.
∵AB=BP=AP=2,∠BOP=90°,
∴OA=OB=1,OP==.
∴ A(-1,0),B(1,0),
P(0, ). (答案不唯一)
(2)当△PAB 是等腰直角三角形时,建立如图2所示的平面直角坐标系.
∵PA=PB,
∴∠APB=90°,∠BOP=90°.
∴ OA=OB=OP=1,
∴ A(-1,0),B(1,0),P(0,1)
(答案不唯一)
本课小结
用坐标表示地理位置
利用平面直角坐标系表示地理位置的方法:
(1) 建立平面直角坐标系,选择一个适当的参照点为原
点,确定 x 轴、y 轴及其正方向.
(2) 根据具体问题确定适当的单位长度.
(3) 在坐标平面内画出这些点,写出各点的坐标和各个
地点的名称.
另外表示地理位置的方法还有:
方位角和距离定位法、网格定位法、区域定位法、经纬定位法等,不管哪种定位法,都需要两个独立的条件.
读一读
有趣的坐标系
如果平面直角坐标系中点的横坐标、纵坐标表示某种实际意义的量那么我们就能设计出一些有趣的坐标系,来表达自然界和人类社会中的一些现象或规律.
在图(1)的平面直角坐标系中,横坐标表示“年人口自然增长率”,纵坐标表示“预期寿命”.
你能写出图中“中国”、“英国”、“世界”、“孟加拉国”这些点的坐标吗 你能说明这些点的坐标的实际含义吗
某地一名中学生在完成了对自家院子里的土壤结构组成的勘测后,用图(2)的坐标
系表示他勘测的结果: 空气
为 22%,固体颗粒为 50%,
水为28%. 你知道这个坐标
系所表示的意义和规律吗
找一找,你的周围有没有一些事物或现象是可以用坐标来表示的.
5 . 2
平面直角坐标系
第2课时
用坐标表示平移
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
1、平移的定义
回顾旧知
(2) 经过平移后,对应点所连的线段 平行且相等;
2、平移的性质
(1) 平移不改变图形的形状和大小,只改变形图
形的位置.
例3 如图,点B、点C在轴上,试在第一象限内画以BC 为底、面积为 10 的等腰三角形ABC,并写出点 A、点 B、点 C的坐标.
解:点 B、C的坐标分别为B(1,0)、C(5,0),BC=4.根据题意,可知等腰三角形 ABC的高为5,点A在 BC 的垂直平分线上,它的横坐标为 3,纵坐标为 5,即 A(3,5).所画ABC 如图.
A
讨 论
在图中,把△ABC 沿 y 轴翻折得到△A′B′C′,再把△A′B′C′ 向下平移3个单位长度得到△A″B″C″. 你能写出△A′B′C′ 、△A″B″C″、各顶点的坐标吗
A′
B′
C′
A″
B″
C″
A′
B′
C′
A″
B″
C″
A′ (-3,5),
B′ (-1,0),
C′ (-5,0).
A″ (-3,2),
B″ (-1,-3),
C″ (-5,-3).
数学实验室
1. 在图5-10 的平面直角坐标系中,依次连接以下各点(最后一点不再与其他点连接),将得到一个怎样的图形
(0.5,4),(0,0),(1,3),
(2,3),(3,2),(3,0),
(1,-1),(2,-1),
(1,-3),(0,-1),
(-1,-3),(-2,-1),
(-1,-1),(-3,0),
(-3,2),(-2,3),
(-1,3),(0,0),(-0.5,4).
如图所示,得到的图案是一只蝴蝶.
2. 观察所画图形,填空:
(1)点(1,-3)关于x 轴对称的点的坐标为_________,关于 y 轴对称的点的坐标为___________;
(1,3)
(-1,-3)
(2)点(-1,3)关于 x 轴对称的点的坐标为__________,关于 y 轴对称的点的坐标为___________.
一般地,点 P(a,b)关于x 轴对称的点的坐标为______,关于 y 轴对称的点的坐标为________.
(-1,-3)
(1,3)
(a,-b)
(-a,b)
3. 在图 5-11中,把线段 AB 先向右平移 7个单位长度,再向上平移 2个单位长度,得到线段 A′B′. 试分别写出点A、B、A′、B′的坐标.
A(-4,1),B(-2,3),
A′(3,3),B′(5,5).
A′
B′
(1) 你能说出点A与点A′、点 B与点 B′的坐标之间的关系吗
A′
B′
点A′的横坐标比点A的横坐标大7,点A′的纵坐标比点A的纵坐标大 2;点B′的横坐标比点B 的横坐标大 7,点B′的纵坐标比点B′的纵坐标大2.
(2) 如果点C(m,n)是线段AB 上的任意一点,那么当AB 平移到A′B′后,写出与点 C 对应的点C′的坐标.
A′
B′
C′ (m+7,n+2).
思 考
如果一个点的纵坐标不变,横坐标改变,那么这个点的位置发生怎样的变化 如果一个点的横坐标不变,纵坐标改变呢
如果一个点的纵坐标不变,横坐标改变,那么该点将向左或向右平移;如果一个点的横坐标不变,纵坐标改变,那么该点将向上或向下平移.
在平面直角坐标系中,点P(a,b)向右(或向左)平移n(n>0)个单位长度,则点P 的纵坐标不变,横坐标加上(或减去)n;
点P(a,b)向上(或向下)平移n(n>0)个单位长度,则点P 的横坐标不变,纵坐标加上(或减去)n.
规 律 总 结
点 P(a,b) 关于 x 轴对称的点的坐标为(a,-b),关于 y 轴对称的点的坐标为(-a,b),关于原点对称的点的坐标为(-a,-b).
将点P(a,b)绕原点旋转180°,得P′(-a,b).
平面内点P(a,b)到原点O 的距离OP=.
练 4
在平面直角坐标系中,点M 的坐标为(1,-3).如果把点M 先向左平移5 个单位长度,再向上平移3 个单位长度得到点M′,则M′的坐标为( )
A. (6,0) B. (6,- 6)
C. (- 4,0) D. (- 4,- 6)
C
练 5
如果点 P (-2,b)和点 Q (a,-3) 关于x 轴对称,则a+b 的值是( )
A. -1 B . 1
C . -5 D . 5
B
练 习
(1) 写出图①中点A、B、M、N
的坐标;
A (2,3),B (3,0),
M (1,1.5),N (2.5,1.5).
(2) 指出图①经过怎样的运动可以得到图②、图③、图④,并分别写出这3 个图中
与点 A、B、M、N 对应的
点A′、B′、M′、N′的坐标.
图②是由图①向右平移 2 个单位长度得到的;
图②中A′(4,3),B′(5,0),M′(3,1.5),N′(4.5,1.5)
图③是由图①沿x轴翻折得到的;
图中A′(2,-3),B′(3,0),M′(1,-1.5),N′(2.5,-1.5)
图④是由图①以点O为中心,顺时针旋转 90°得到的.
图④中A′(3,-2),B′(0,-3),M′(1.5,-1),N′(1.5,-2.5).
本课小结
用坐标表示平移
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
第3课时
用坐标表示地理位置
在茫茫的大海上,“北斗导航系统能对渔船进行准确定位. ”以便及时掌握各种情况.这个系统是怎样定位的呢,答案就在本节中.
思 考
如图 5-12,电视机厂通过由电脑控制的机械手,把各种元器件准确插入线路板上的焊孔,然后通过焊接工序将它们焊牢.
如果你是工程师,那么你怎样向机械手下达指令,使它把元器件准确插入相应的焊孔?
如果在线路板上建立平面直角坐标系,用坐标表示焊孔 A、B 的位置,那么向电脑输入点 A、B 的坐标后,机械手就会按坐标指示的“地址”将有关元器件准确插入焊孔 A、B.
例如,建立如图 5-13 的平面直角坐标系,则点 A 的坐标为(a,d),点B的坐标为(b,c).
(1) 选择一个适当的点为原点;
(2) 过原点在两个互相垂直的方向上分别作出
x 轴、y 轴;
(3) 根据具体问题确定单位长度.
建立平面直角坐标系的一般步骤
(1) 坐标轴的方向通常取水平方向为x轴,竖直方向为y轴;
(2)平面直角坐标系变化时,坐标平面内各点的坐标也发生变化,但各点之间的相对位置并不会发生变化.
特别解读
尝 试
在图5-14 中,以“中心广场”为坐标原点,以正东方向为 x 轴正方向、正北方向为 y 轴正方向,画出平面直角坐标系. 说出各旅游景点的位置 (小方格的边长为 1个长度单位).
画平面直角坐标系如图所示.
O(0,0),A(5,7),B(-8,5),C(-11,1),D(-8,-3),E(-12,-8),F(3,-6)
例4 已知正方形 ABCD 的边长为 4,建立适当的平面直角坐标系,分别写出各顶点的坐标.
解:如图 ,以点 A 为坐标原点,分别以边 AB、AD所在直线为x轴、y轴建立平面直角坐标系,点A的坐标为(0,0).
∵ AB=AD=4,
∴ 点B的坐标为(4,0),
点 D的坐标为(0,4).
∵ DC=AB,BC=AD,
∴ 点C的坐标为(4,4).
讨 论
还能建立不同的平面直角坐标系表示例4中正方形各顶点的坐标吗
根据实际问题的需要,建立恰当的平面直角坐标系,可以使一些点的坐标较为简明,便于研究和解决问题.
练 6
根据下面的条件画一幅示意图,并在图中标出各个景点的位置和坐标.
菊花园:从中心广场向北走150 m,再向东走150 m;
湖心亭:从中心广场向西走150 m,再向北走100 m;
松风亭:从中心广场向西走100 m,再向南走50 m;
育德泉:从中心广场向北走200 m.
练 习
1. 根据某动物园的平面示意图,以大门所在的位置为坐
标原点,以正东方向为x 轴正方向、正北方向为 y 轴
正方向,以l cm为单位长度,建立平面直角坐标系,
用坐标表示猴山、驼峰、百鸟园和熊猫馆的位置。
略
2. 在△PAB 中,PA=PB,AB=2. 建立适当的平面直角
坐标系,分别写出△PAB 是等边三角形、等腰直角三
角形时各顶点的坐标.
解:(1)当△PAB 是等边三角形时,建立如图1所示的平面直角坐标系.
∵AB=BP=AP=2,∠BOP=90°,
∴OA=OB=1,OP==.
∴ A(-1,0),B(1,0),
P(0, ). (答案不唯一)
(2)当△PAB 是等腰直角三角形时,建立如图2所示的平面直角坐标系.
∵PA=PB,
∴∠APB=90°,∠BOP=90°.
∴ OA=OB=OP=1,
∴ A(-1,0),B(1,0),P(0,1)
(答案不唯一)
本课小结
用坐标表示地理位置
利用平面直角坐标系表示地理位置的方法:
(1) 建立平面直角坐标系,选择一个适当的参照点为原
点,确定 x 轴、y 轴及其正方向.
(2) 根据具体问题确定适当的单位长度.
(3) 在坐标平面内画出这些点,写出各点的坐标和各个
地点的名称.
另外表示地理位置的方法还有:
方位角和距离定位法、网格定位法、区域定位法、经纬定位法等,不管哪种定位法,都需要两个独立的条件.
读一读
有趣的坐标系
如果平面直角坐标系中点的横坐标、纵坐标表示某种实际意义的量那么我们就能设计出一些有趣的坐标系,来表达自然界和人类社会中的一些现象或规律.
在图(1)的平面直角坐标系中,横坐标表示“年人口自然增长率”,纵坐标表示“预期寿命”.
你能写出图中“中国”、“英国”、“世界”、“孟加拉国”这些点的坐标吗 你能说明这些点的坐标的实际含义吗
某地一名中学生在完成了对自家院子里的土壤结构组成的勘测后,用图(2)的坐标
系表示他勘测的结果: 空气
为 22%,固体颗粒为 50%,
水为28%. 你知道这个坐标
系所表示的意义和规律吗
找一找,你的周围有没有一些事物或现象是可以用坐标来表示的.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
