2023-2024学年苏科版数学八年级上册6.1 函数 课件(共40张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册6.1 函数 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 49.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 18:01:34 | ||
图片预览









文档简介
(共40张PPT)
6 . 1
函 数
课时导入
一辆长途客车从杭州驶向
上海,全程哪些量不变?
哪些量在变?
第1课时
变 量
列车从甲地驶往乙地,在 16∶17 到16∶22 这个时段列车行驶过程中,哪些量没有变化 哪些量不断变化
在这个时段里,电子显示屏上的“200km/h”没变过.
列车行驶的时间在不断变化.
甲、乙两地间的路程不变.
列车离甲地越来越远离乙地越来越近.
常量与变量
在某一变化过程中,数值保持不变的量叫做常量,
可以取不同数值的量叫做变量.
例如,在上述的列车行驶过程中,列车行驶的速度,甲、乙两地的路程是常量;列车行驶的时间,列车离甲、乙两地间的路程是变量.
(1) “常量”是已知数,是指在整个变化过程中保持不变的量;但“常量”不等于“常数”,它可以是数值不变的字母. 如在匀速运动中的速度v 就是一个常量.
(2) 变量与常量是相对的,前提是“在一个变化过程中”,一个量在某一变化过程中是常量,而在另一个变化过程中,它可能是变量. 如在 s=vt 中,当s 一定时,v 和t 为变量,s 为常量;当t 一定时,s 和v 为变量,t 为常量.
1. 变量、常量与字母的指数没有关系,如
y=100-2x2
中,x,y 是变量,而不能说x2 是变量;
2. 指出一个变化过程中的常量时,应连同它前面的符号.
特别提醒:
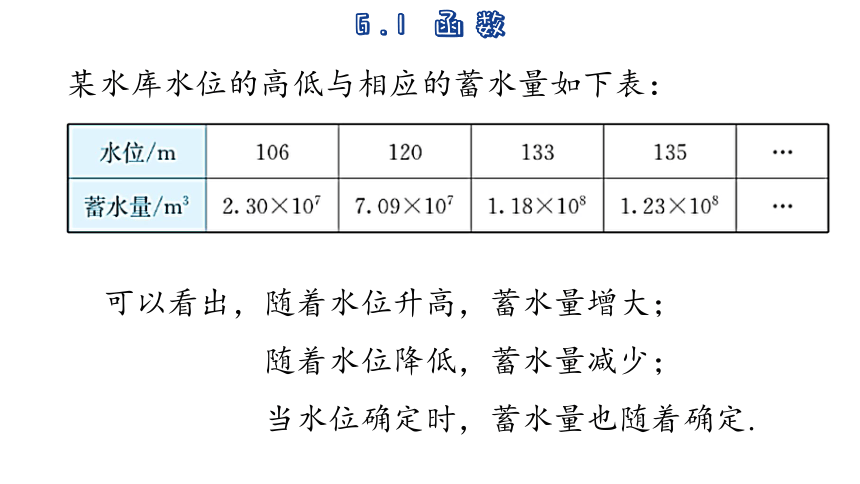
某水库水位的高低与相应的蓄水量如下表:
可以看出,随着水位升高,蓄水量增大;
随着水位降低,蓄水量减少;
当水位确定时,蓄水量也随着确定.
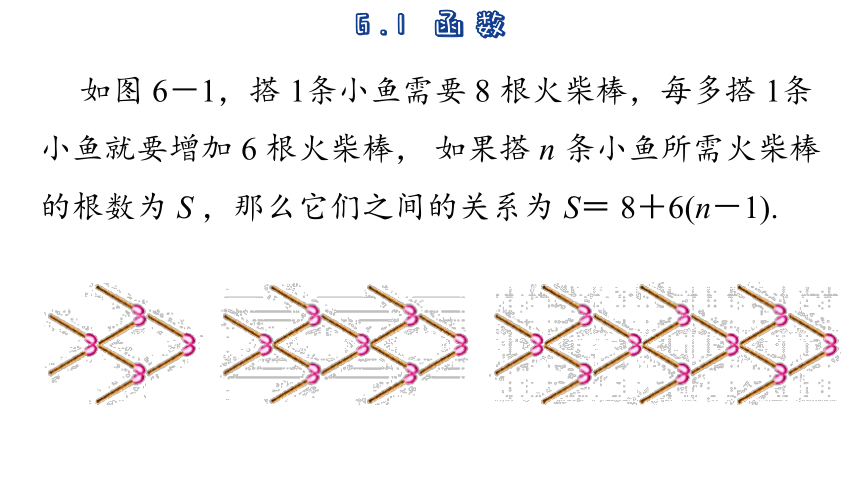
如图 6-1,搭 1条小鱼需要 8 根火柴棒,每多搭 1条小鱼就要增加 6 根火柴棒, 如果搭 n 条小鱼所需火柴棒的根数为 S ,那么它们之间的关系为 S= 8+6(n-1).
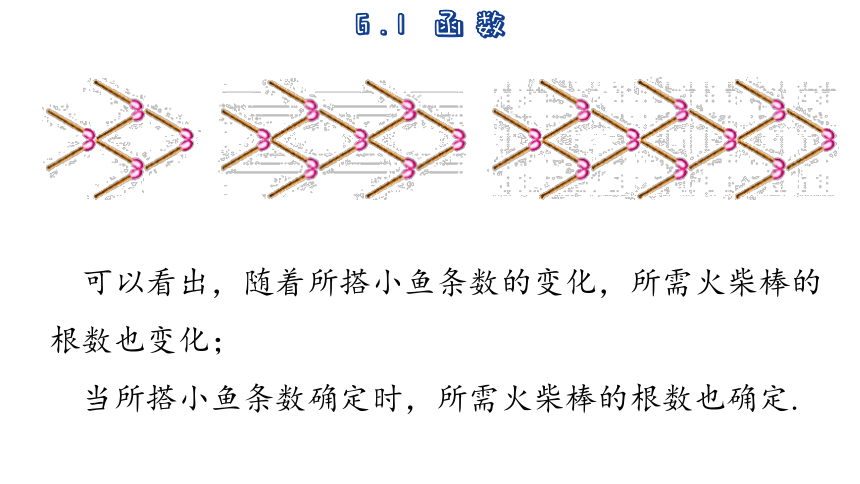
可以看出,随着所搭小鱼条数的变化,所需火柴棒的根数也变化;
当所搭小鱼条数确定时,所需火柴棒的根数也确定.
如图 6-2,把水滴激起的波纹看成是一个不断向外扩展的圆,它的面积随着半径的变化而变化,随着半径的确定而确定.
上述的每个变化过程中都有两个变量,并且其中一个变量变化时另一个变量也随着变化;一个变量确定时,另一个变量也随着确定.
尝 试
你还能举出一些类似的实例吗
一天的气温随着一天时间的变化而变化;
汽车在路上匀速行驶时,行驶的路程,随时间的变化而变化等.(答案不唯一)
练 1
分别指出下列关系中的变量和常量:
(1) 圆面积公式 S=πr2 (S表示面积,r表示半径);
(2) 在三角形ABC中,它的底边长a一定,底边上的高
是h, 则三角形的面积 S=ah.
解:r,S是变量,π是常量;
解:S,h 是变量, ,a是常量.
本课小结
变 量
判断一个量是常量还是变量的方法:
看这个量所在的变化过程中.该量的值是否发生改变(或者说是否会取不同的数值).其中在变化过程中,数值始终不变的量是常量,可以取不同数值的量是变量.
第2课时
函 数
根据经验,跳远的距离 s=0.085v2(v是助跑的速度,0<v<10.5米/秒),其中变量s随着哪一个量的变化而变化?
一般地,在一个变化过程中的两个变量 x 和 y ,如果对于x的每一个值,y 都有唯一的值与它对应,那么我们称 y 是 x 的函数,x 是自变量.
函 数
例如,在上面的实际例子中,水库蓄水量是水位高低的函数,搭“小鱼”所需火柴棒的根数是所搭“小鱼”条数的函数,圆面积是圆半径的函数.
交 流
用一根长 2 m 的铁丝围成一个长方形.
(1) 当长方形的宽为 0.1m时,长为多少
当长方形的宽为 0.1 m 时,长为:
×(2-0.1×2)=0.9 (m).
(2) 当长方形的宽为 0.2m时,长为多少
当长方形的宽为 0.2 m 时,长为:
×(2-0.2×2)=0.8 (m).
(3) 这个长方形的长是宽的函数吗 为什么
长方形的周长一定时,长是宽的函数. 因为当长方形的周长一定时,长随宽的变化而变化,对于宽的每一个确定值,长都有唯一的值与它对应,所以这个长方形的长是宽的函数.
练 习
1.“沙漏”是我国古代一种计量时间的仪器 ,它
根据一个容器里的细沙漏到另一个容器中的数量来
计量时间 . 请说出这个变化过程中的自变量.
解:在这一变化过程中,时间是随细沙流动的数量来确定的,故时间是细沙流动的数量的函数细沙从一个容器漏到另一个容器中的数量是自变量.
2. 按图示的运算程序,每输入一个实数 ,
便可输出一个对应的实数 y. y是 x 的函
数吗 为什么
解:y是x的函数由运算程序可得 y=5(x+2) -4=5x+6,显然,对于x的每一个值,y都有唯一的值与它对应,符合函数的定义,所以,是的函数.
交 流
汽车以 100 km/h 的速度匀速行驶,行驶的时间为 t (h),行驶的路程为 y (km),怎样表示 y与 t 的关系
可以列表表示.
可以在平面直角坐标系中画图表示.
可以列式表示.
y=100t .
像 y=100t、S=8+6(n-1)等表示两个变量之间函数关系的式子称为函数表达式.
例1 汽车油箱内有油 40 L,每行驶100km耗油10L,求行驶过程中油箱内剩余油量 Q (L) 与行驶路程 s (km)的函数表达式.
解:汽车行驶100 km 耗油10 L,行驶 s km 耗油 10 L,所以Q(L)与s(km)之间的函数表达式为:
Q = 40 - 10 ,即 Q = 40 - .
思 考
汽车行驶 250 km 时,油箱里还有多少油
就是计算当s=250时代数式 40- 的值.
当s=250时,Q=40-250=15(L),即油箱里还有15 L油.
在太阳和月球引力的影响下,海水定时涨落的现象称为海洋潮沟涨落的水位高低称为潮位。图6-4 是我国某海港某天的实时潮位图.
在图6-4中,潮位仪绘制的平滑曲线,揭示了这一天潮位 y (m)与时间 t (h)之间的函数关系.
像这样,在平面直角坐标系中,以函数的自变量的值为横坐标、对应的函数值为纵坐标的点所组成的图形叫做这个函数的图像.
例2 小明骑自行车从甲地到乙地,图 6-5 中的折线表示小明行驶的路程 s (km)与所用时间 t (h)之间的函数关系。试根据函数图像回答下列问题:
(1) 小明从甲地到乙地用了多少时间
解:小明从甲地到乙地用了7h.
(2) 小明出发 5 h 时,距离甲地多少路程
当t=5时,s=30.小明出发5 h时,距离甲地30 km.
(3) 折线中有一条平行于 t 轴的线段,它的意义是什么
当t从2变化到4 时,s的值不变,说明小明在途中滞留了2h.
在实际问题中,自变量的取值通常有一定的范围.
例如,例1中自变量 s 的取值范围是 0≤t≤400,
例2中自变量 t 的取值范围是 0≤t≤7.
练 习
1. 商店有 100 支铅笔. 如果卖出 x 支,还剩 y 支,
那么 y=________________________________;
当 x 的值越来越大时,y的值会发生什么变化
100-x (0<x<100,x为自然数)
当 x 的值越来越大时,y 的值越来越小,直至为0.
2. 甲、乙两人出门散步,用 20 min走了900 m后,甲随即按原速返回;乙遇到一位朋友,并与朋友交谈了 10 min 后,用 15 min 回到家里. 在下列 4 个图像中,哪一个表示甲离家的路程 s (m)与时间 t (min)之间的函数关系 哪一个表示乙离家的路程与时间之间的函数关系
解:图②表示甲离家的路程 s(m)与时间t(min)之间的函数关系.
解:图④表示乙离家的路程 s(m)与时间t(min)之间的函数关系.
本课小结
函 数
1.函数:在变化过程中,有两个变量x和y,并且对
于每一个x的值,y都有唯一的值与其对应.
2. 自变量的取值范围要使所给函数解析式有意义.
3. 函数值:
如果在自变量取值范围内给定一个数值a,函数对应的值为b,那么b叫做自变量的值为a时的函数值.
6 . 1
函 数
课时导入
一辆长途客车从杭州驶向
上海,全程哪些量不变?
哪些量在变?
第1课时
变 量
列车从甲地驶往乙地,在 16∶17 到16∶22 这个时段列车行驶过程中,哪些量没有变化 哪些量不断变化
在这个时段里,电子显示屏上的“200km/h”没变过.
列车行驶的时间在不断变化.
甲、乙两地间的路程不变.
列车离甲地越来越远离乙地越来越近.
常量与变量
在某一变化过程中,数值保持不变的量叫做常量,
可以取不同数值的量叫做变量.
例如,在上述的列车行驶过程中,列车行驶的速度,甲、乙两地的路程是常量;列车行驶的时间,列车离甲、乙两地间的路程是变量.
(1) “常量”是已知数,是指在整个变化过程中保持不变的量;但“常量”不等于“常数”,它可以是数值不变的字母. 如在匀速运动中的速度v 就是一个常量.
(2) 变量与常量是相对的,前提是“在一个变化过程中”,一个量在某一变化过程中是常量,而在另一个变化过程中,它可能是变量. 如在 s=vt 中,当s 一定时,v 和t 为变量,s 为常量;当t 一定时,s 和v 为变量,t 为常量.
1. 变量、常量与字母的指数没有关系,如
y=100-2x2
中,x,y 是变量,而不能说x2 是变量;
2. 指出一个变化过程中的常量时,应连同它前面的符号.
特别提醒:
某水库水位的高低与相应的蓄水量如下表:
可以看出,随着水位升高,蓄水量增大;
随着水位降低,蓄水量减少;
当水位确定时,蓄水量也随着确定.
如图 6-1,搭 1条小鱼需要 8 根火柴棒,每多搭 1条小鱼就要增加 6 根火柴棒, 如果搭 n 条小鱼所需火柴棒的根数为 S ,那么它们之间的关系为 S= 8+6(n-1).
可以看出,随着所搭小鱼条数的变化,所需火柴棒的根数也变化;
当所搭小鱼条数确定时,所需火柴棒的根数也确定.
如图 6-2,把水滴激起的波纹看成是一个不断向外扩展的圆,它的面积随着半径的变化而变化,随着半径的确定而确定.
上述的每个变化过程中都有两个变量,并且其中一个变量变化时另一个变量也随着变化;一个变量确定时,另一个变量也随着确定.
尝 试
你还能举出一些类似的实例吗
一天的气温随着一天时间的变化而变化;
汽车在路上匀速行驶时,行驶的路程,随时间的变化而变化等.(答案不唯一)
练 1
分别指出下列关系中的变量和常量:
(1) 圆面积公式 S=πr2 (S表示面积,r表示半径);
(2) 在三角形ABC中,它的底边长a一定,底边上的高
是h, 则三角形的面积 S=ah.
解:r,S是变量,π是常量;
解:S,h 是变量, ,a是常量.
本课小结
变 量
判断一个量是常量还是变量的方法:
看这个量所在的变化过程中.该量的值是否发生改变(或者说是否会取不同的数值).其中在变化过程中,数值始终不变的量是常量,可以取不同数值的量是变量.
第2课时
函 数
根据经验,跳远的距离 s=0.085v2(v是助跑的速度,0<v<10.5米/秒),其中变量s随着哪一个量的变化而变化?
一般地,在一个变化过程中的两个变量 x 和 y ,如果对于x的每一个值,y 都有唯一的值与它对应,那么我们称 y 是 x 的函数,x 是自变量.
函 数
例如,在上面的实际例子中,水库蓄水量是水位高低的函数,搭“小鱼”所需火柴棒的根数是所搭“小鱼”条数的函数,圆面积是圆半径的函数.
交 流
用一根长 2 m 的铁丝围成一个长方形.
(1) 当长方形的宽为 0.1m时,长为多少
当长方形的宽为 0.1 m 时,长为:
×(2-0.1×2)=0.9 (m).
(2) 当长方形的宽为 0.2m时,长为多少
当长方形的宽为 0.2 m 时,长为:
×(2-0.2×2)=0.8 (m).
(3) 这个长方形的长是宽的函数吗 为什么
长方形的周长一定时,长是宽的函数. 因为当长方形的周长一定时,长随宽的变化而变化,对于宽的每一个确定值,长都有唯一的值与它对应,所以这个长方形的长是宽的函数.
练 习
1.“沙漏”是我国古代一种计量时间的仪器 ,它
根据一个容器里的细沙漏到另一个容器中的数量来
计量时间 . 请说出这个变化过程中的自变量.
解:在这一变化过程中,时间是随细沙流动的数量来确定的,故时间是细沙流动的数量的函数细沙从一个容器漏到另一个容器中的数量是自变量.
2. 按图示的运算程序,每输入一个实数 ,
便可输出一个对应的实数 y. y是 x 的函
数吗 为什么
解:y是x的函数由运算程序可得 y=5(x+2) -4=5x+6,显然,对于x的每一个值,y都有唯一的值与它对应,符合函数的定义,所以,是的函数.
交 流
汽车以 100 km/h 的速度匀速行驶,行驶的时间为 t (h),行驶的路程为 y (km),怎样表示 y与 t 的关系
可以列表表示.
可以在平面直角坐标系中画图表示.
可以列式表示.
y=100t .
像 y=100t、S=8+6(n-1)等表示两个变量之间函数关系的式子称为函数表达式.
例1 汽车油箱内有油 40 L,每行驶100km耗油10L,求行驶过程中油箱内剩余油量 Q (L) 与行驶路程 s (km)的函数表达式.
解:汽车行驶100 km 耗油10 L,行驶 s km 耗油 10 L,所以Q(L)与s(km)之间的函数表达式为:
Q = 40 - 10 ,即 Q = 40 - .
思 考
汽车行驶 250 km 时,油箱里还有多少油
就是计算当s=250时代数式 40- 的值.
当s=250时,Q=40-250=15(L),即油箱里还有15 L油.
在太阳和月球引力的影响下,海水定时涨落的现象称为海洋潮沟涨落的水位高低称为潮位。图6-4 是我国某海港某天的实时潮位图.
在图6-4中,潮位仪绘制的平滑曲线,揭示了这一天潮位 y (m)与时间 t (h)之间的函数关系.
像这样,在平面直角坐标系中,以函数的自变量的值为横坐标、对应的函数值为纵坐标的点所组成的图形叫做这个函数的图像.
例2 小明骑自行车从甲地到乙地,图 6-5 中的折线表示小明行驶的路程 s (km)与所用时间 t (h)之间的函数关系。试根据函数图像回答下列问题:
(1) 小明从甲地到乙地用了多少时间
解:小明从甲地到乙地用了7h.
(2) 小明出发 5 h 时,距离甲地多少路程
当t=5时,s=30.小明出发5 h时,距离甲地30 km.
(3) 折线中有一条平行于 t 轴的线段,它的意义是什么
当t从2变化到4 时,s的值不变,说明小明在途中滞留了2h.
在实际问题中,自变量的取值通常有一定的范围.
例如,例1中自变量 s 的取值范围是 0≤t≤400,
例2中自变量 t 的取值范围是 0≤t≤7.
练 习
1. 商店有 100 支铅笔. 如果卖出 x 支,还剩 y 支,
那么 y=________________________________;
当 x 的值越来越大时,y的值会发生什么变化
100-x (0<x<100,x为自然数)
当 x 的值越来越大时,y 的值越来越小,直至为0.
2. 甲、乙两人出门散步,用 20 min走了900 m后,甲随即按原速返回;乙遇到一位朋友,并与朋友交谈了 10 min 后,用 15 min 回到家里. 在下列 4 个图像中,哪一个表示甲离家的路程 s (m)与时间 t (min)之间的函数关系 哪一个表示乙离家的路程与时间之间的函数关系
解:图②表示甲离家的路程 s(m)与时间t(min)之间的函数关系.
解:图④表示乙离家的路程 s(m)与时间t(min)之间的函数关系.
本课小结
函 数
1.函数:在变化过程中,有两个变量x和y,并且对
于每一个x的值,y都有唯一的值与其对应.
2. 自变量的取值范围要使所给函数解析式有意义.
3. 函数值:
如果在自变量取值范围内给定一个数值a,函数对应的值为b,那么b叫做自变量的值为a时的函数值.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
