2023-2024学年苏科版数学八年级上册4.3 实数 课件(共51张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册4.3 实数 课件(共51张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 56.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 18:04:42 | ||
图片预览






文档简介
(共51张PPT)
4 . 3
实 数
回顾旧知
什么是有理数?有理数怎样分类?
有理数
整 数
分 数
有理数
正有理数
负有理数
0
第1课时
实数及其分类
尝 试
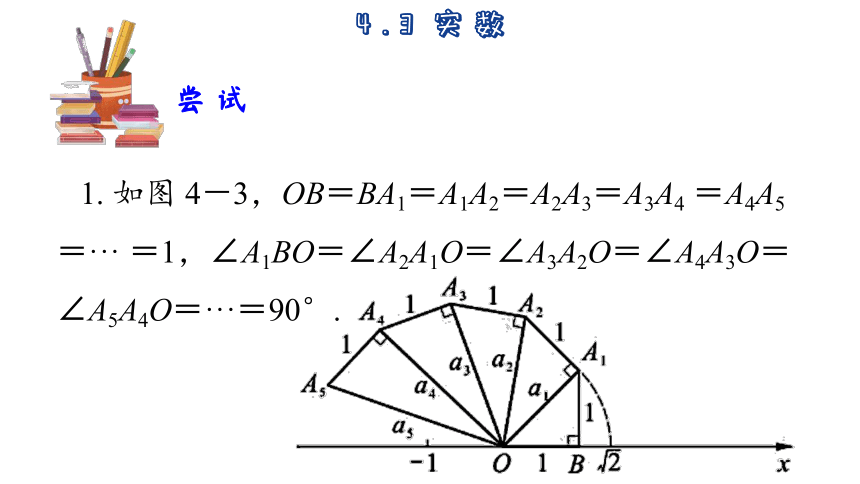
1. 如图 4-3,OB=BA1=A1A2=A2A3=A3A4 =A4A5=··· =1,∠A1BO=∠A2A1O=∠A3A2O=∠A4A3O=∠A5A4O=···=90°.
试计算 a12、a22、a32、a42、a52,你能说出 a1、a2、a3、a4、a5 的值吗
a1=,a2 = ······
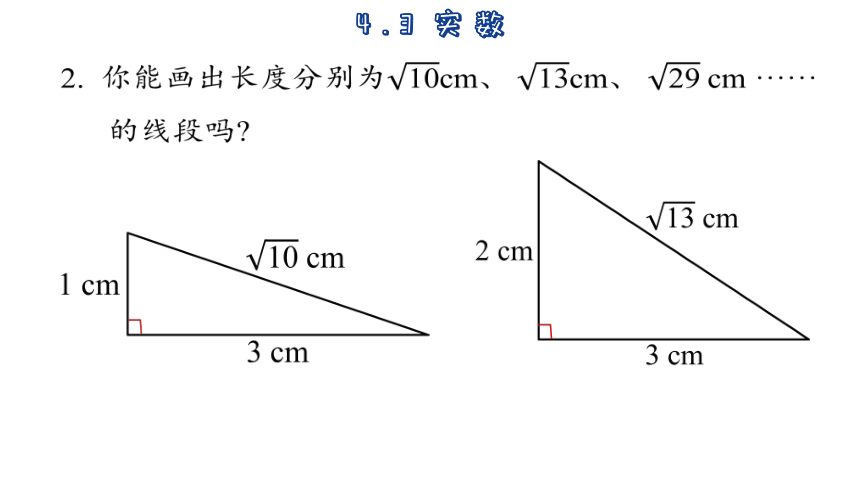
2. 你能画出长度分别为cm、 cm、 cm ······
的线段吗
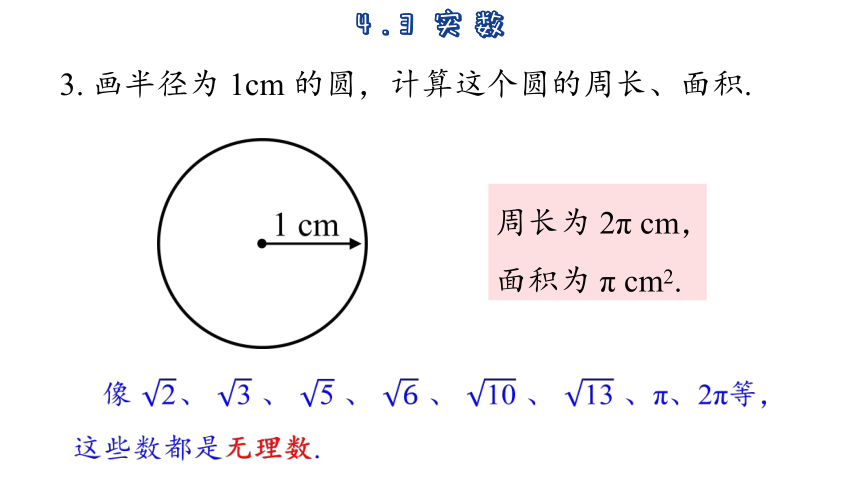
3. 画半径为 1cm 的圆,计算这个圆的周长、面积.
周长为 2π cm,
面积为 π cm2.
像 、 、 、 、 、 、π、2π等,这些数都是无理数.
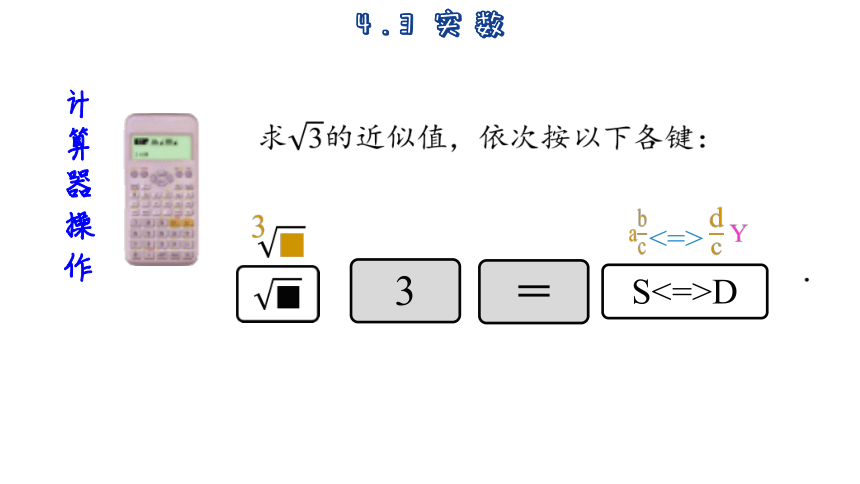
计算器操作
求的近似值,依次按以下各键:
·
3
=
S<=>D
a
Y
<=>
知识点 1 无理数
定义:
无限不循环小数叫做无理数.
小数位数无限,小数形式为不循环.
判断标准
(1) 开方开不尽的数,如 , ,···;
(2) 含有π的一类数: π, π,π+1,···;
(3) 以无限不循环小数的形式出现的特定结构的数,如 0.101 001 000 1…(每相邻两个1之间依次多一个0)
三种常见形式:
(1) 无理数都是无限小数,但无限小数不一定是无理数;
(2) 带根号的数不一定都是无理数,不带根号的数也不一定就是有理数.
易错提醒:
知识点 2 实 数
有理数和无理数统称为实数.
实数的概念
实数可以分类如下:
实数
有理数
无理数
正有理数
负有理数
0
正无理数
负无理数
有限小数或循环小数
无限不循环小数
练 1
把下列各数填入相应的集合内:
-, -,, , - ,0, -π, -,
-4.0,3.1010010001···(每相邻两个1之间0的个数逐次加1)
有理数集合:{ … } ;
无理数集合:{ … } ;
整数集合:{ … } ;
分数集合:{ … } ;
正实数集合:{ … } ;
负实数集合:{ … }
-,,-,0,-,-4.0
-,,-π,-,3.1010010001···
- ,0,
-, , -,-4.0
, ,- ,3.1010010001···
-,-,-,-π,-,-4.0
无理数可以用数轴上的点来表示,例如,在图 4-4 中,点 A 表示,点 B 表示.
知识点 3 实 数与数轴
探 索
试在图 4-4 中画出表示、 的点.
如图所示,点 C 表示 ,点 D 表示 .
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数,实数与数轴上的点一一对应.
实数与数轴间的关系:
可用两点所表示的实数来表示,即点A、点B 在数轴上表示的实数分别为x1、x2,
则 AB= |x1-x2| .
数轴上两点间的距离
练 2
请在如图所示的数轴上分别作出表示 - 和 的点.
解: 如图, 表示- 和 的点分别是A、B.
练 2
点 A 在数轴上表示的数为 3 ,点B 在数轴上表示的数为-5,则A、B两点之间的距离为 .
解:由题意得︱ 3-(- 5 )︱ = 3 + 5 .
练 习
把下列各数填入相应的括号内:
4 ,-,0.,,,, , -,0.010 010 001 000 01···.
(1) 有理数:{ ···};
(2) 无理数:{ ···};
(3) 正实数:{ ···};
(4) 负实数:{ ···};
4 ,0.,,,-,
-,, , 0.010 010 001 000 01···
4 ,0.,,, ,0.010 010 001 000 01···
-,,-,
本课小结
实数及其分类
1、无限不循环的小数 叫做无理数.
有理数和无理数统称实数.
2、实数与数轴上的点是一一对应的.
3、同样的,平面直角坐标系中的点与有序实数对是
一一对应的.
第2课时
实数的性质
有理数的绝对值、相反数、倒数的意义,有理数大小比较的方法有理数的运算性质、运算律,在实数范围内都仍然适用.
在实数范围内,不仅可以进行加、减、乘、除、乘方运算,而且可以进行开立方运算以及非负实数的开平方运算.
知识点 4 实数的性质
思考
(1) 的相反数是________,-π的相反数是______,
0的相反数是______;
(2) | | = _______, |-π|=______, |0|= ______.
π
0
π
0
-
(1) 相反数:实数a 的相反数为-a,若a、b 互为相反数,则a+b=0;
(2) 倒数:非零实数 a 的倒数为 , 若a、b 互为倒数,则 ab=1;
相关概念
|a|=
a (a≥0),
a (a<0),
在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
(2) 对实数的有关概念进行辨析时,错误的说法只需举一个反例即可.
特别提醒:
比较实数的大小
(1) 定义法:正数大于0,负数小于0,
正数大于一切负数;
(2) 性质法:两个正数, 绝对值大的数大;
两个负数,绝对值大的数反而小.
练 3
求下列各数的相反数、倒数和绝对值.
(1) , (2) - ,(3) , (4) 2- .
相反数:
倒数:
绝对值:
-
-
-
-2
2-
知识点 5 实数的运算
1. 在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
2. 实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c=a(bc);
乘法分配律:(a+b)c=ac+bc.
练 4
计算:
(1) +|-6| -22; (2) ()-1 +( -1)0 - ;
(3) -(-1)2 -(π -1)0+2-1.
解:(1)原式=2+6 - 4=4.
(2) 原式=3+1 - 2=2.
(3) 原式=2 -1-1+ = .
例1 用计算器比较-与- 的大小.
解:依次按以下各键: ,
计算器显示的结果为- 2.080 083 823.
依次按以下各键:
,
计算器显示的结果为- 2.080 024 038.
因为- 2.080083 823 < - 2.080 024 038,
所以-< - .
例2 用计算器计算:
(1) +π; (2) 3×- ;
(3) +3-(+ ).
解:(1) 依次按以下各键:
计算器显示的结果为 5.377 660 631,
即 + π ≈5.377 660 631;
解:(2)依次按以下各键:
,
计算器显示的结果为 2.982 719 637,
即3×- ≈2.982 719 637;
(2) 3×- ;
(3) +3-(+ ).
解:+3-(+ ) = +3--
= 3-.
依次按以下各键:
计算器显示的结果为 0.763 932 022 5,
即+3-(+ ) ≈ 0.763 932 0225.
交 流
先通过估算比较下列各组数的大小,再用计算器验证:
(1) -与-1.5;
| - | = ,| -1.5 | = 1.5,
∵()2=3 > 1.52 =2.25,
∴ | - | > | -1.5 | ,
∴ -< - 1.5.
(2) 与0.5.
∵5 >4,
∴ > 2,
∴ > 1,
∴ > ,即 >0.5.
练 习
1. 估算(精确到个位):
(1) ; (2) .
解:(1)∵64<68<72.25,
∴8<<8.5,
∴ ≈8.
解:(2)∵91.125<120<125,
∴4.5<<5,
∴≈5.
2. 用计算器比较下列各组数的大小:
(1) 与; (2) 与;
(3) 与.
<
>
<
3. 用计算器计算:
(1) 3×-2π; (2) -2×+5× ;
(3) -(+ ).
≈ - 2.040 544 62.
≈ 1.827 469 294.
≈ - 1.555 683 434.
阅 读
证明 是无理数
我们可以用下面的方法证明 是无理数:
假设是有理数,那么可以写成 (m、n是正整数,且没有大于1的公约数),即= .
根据平方根的意义,() = 2,即 =2,2n2=m2.
由于上式左边是偶数,所以右边也是偶数,从而可知 m 是偶数.
设 m=2p(p是正整数),
把 m=2p 代入 2n2=m2,得2n2=4p2,即 n2=2p2.
因此,n也是偶数.
于是,m、n 都是 2的倍数,这与 m、n 没有大于1的公约数相矛盾.
因此,= 是不可能的,也就是说不是有理数,它是无理数.
本课小结
实数的性质
1. 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
3. 在进行实数的运算时,有理数的运算法则及运算性
质同样适用.
2. 实数的大小比较方法有:利用数轴比较、利用绝对
值比较、求平方比较、求差比较、求商比较和计
算近似值比较等方法.
4 . 3
实 数
回顾旧知
什么是有理数?有理数怎样分类?
有理数
整 数
分 数
有理数
正有理数
负有理数
0
第1课时
实数及其分类
尝 试
1. 如图 4-3,OB=BA1=A1A2=A2A3=A3A4 =A4A5=··· =1,∠A1BO=∠A2A1O=∠A3A2O=∠A4A3O=∠A5A4O=···=90°.
试计算 a12、a22、a32、a42、a52,你能说出 a1、a2、a3、a4、a5 的值吗
a1=,a2 = ······
2. 你能画出长度分别为cm、 cm、 cm ······
的线段吗
3. 画半径为 1cm 的圆,计算这个圆的周长、面积.
周长为 2π cm,
面积为 π cm2.
像 、 、 、 、 、 、π、2π等,这些数都是无理数.
计算器操作
求的近似值,依次按以下各键:
·
3
=
S<=>D
a
Y
<=>
知识点 1 无理数
定义:
无限不循环小数叫做无理数.
小数位数无限,小数形式为不循环.
判断标准
(1) 开方开不尽的数,如 , ,···;
(2) 含有π的一类数: π, π,π+1,···;
(3) 以无限不循环小数的形式出现的特定结构的数,如 0.101 001 000 1…(每相邻两个1之间依次多一个0)
三种常见形式:
(1) 无理数都是无限小数,但无限小数不一定是无理数;
(2) 带根号的数不一定都是无理数,不带根号的数也不一定就是有理数.
易错提醒:
知识点 2 实 数
有理数和无理数统称为实数.
实数的概念
实数可以分类如下:
实数
有理数
无理数
正有理数
负有理数
0
正无理数
负无理数
有限小数或循环小数
无限不循环小数
练 1
把下列各数填入相应的集合内:
-, -,, , - ,0, -π, -,
-4.0,3.1010010001···(每相邻两个1之间0的个数逐次加1)
有理数集合:{ … } ;
无理数集合:{ … } ;
整数集合:{ … } ;
分数集合:{ … } ;
正实数集合:{ … } ;
负实数集合:{ … }
-,,-,0,-,-4.0
-,,-π,-,3.1010010001···
- ,0,
-, , -,-4.0
, ,- ,3.1010010001···
-,-,-,-π,-,-4.0
无理数可以用数轴上的点来表示,例如,在图 4-4 中,点 A 表示,点 B 表示.
知识点 3 实 数与数轴
探 索
试在图 4-4 中画出表示、 的点.
如图所示,点 C 表示 ,点 D 表示 .
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数,实数与数轴上的点一一对应.
实数与数轴间的关系:
可用两点所表示的实数来表示,即点A、点B 在数轴上表示的实数分别为x1、x2,
则 AB= |x1-x2| .
数轴上两点间的距离
练 2
请在如图所示的数轴上分别作出表示 - 和 的点.
解: 如图, 表示- 和 的点分别是A、B.
练 2
点 A 在数轴上表示的数为 3 ,点B 在数轴上表示的数为-5,则A、B两点之间的距离为 .
解:由题意得︱ 3-(- 5 )︱ = 3 + 5 .
练 习
把下列各数填入相应的括号内:
4 ,-,0.,,,, , -,0.010 010 001 000 01···.
(1) 有理数:{ ···};
(2) 无理数:{ ···};
(3) 正实数:{ ···};
(4) 负实数:{ ···};
4 ,0.,,,-,
-,, , 0.010 010 001 000 01···
4 ,0.,,, ,0.010 010 001 000 01···
-,,-,
本课小结
实数及其分类
1、无限不循环的小数 叫做无理数.
有理数和无理数统称实数.
2、实数与数轴上的点是一一对应的.
3、同样的,平面直角坐标系中的点与有序实数对是
一一对应的.
第2课时
实数的性质
有理数的绝对值、相反数、倒数的意义,有理数大小比较的方法有理数的运算性质、运算律,在实数范围内都仍然适用.
在实数范围内,不仅可以进行加、减、乘、除、乘方运算,而且可以进行开立方运算以及非负实数的开平方运算.
知识点 4 实数的性质
思考
(1) 的相反数是________,-π的相反数是______,
0的相反数是______;
(2) | | = _______, |-π|=______, |0|= ______.
π
0
π
0
-
(1) 相反数:实数a 的相反数为-a,若a、b 互为相反数,则a+b=0;
(2) 倒数:非零实数 a 的倒数为 , 若a、b 互为倒数,则 ab=1;
相关概念
|a|=
a (a≥0),
a (a<0),
在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
(2) 对实数的有关概念进行辨析时,错误的说法只需举一个反例即可.
特别提醒:
比较实数的大小
(1) 定义法:正数大于0,负数小于0,
正数大于一切负数;
(2) 性质法:两个正数, 绝对值大的数大;
两个负数,绝对值大的数反而小.
练 3
求下列各数的相反数、倒数和绝对值.
(1) , (2) - ,(3) , (4) 2- .
相反数:
倒数:
绝对值:
-
-
-
-2
2-
知识点 5 实数的运算
1. 在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
2. 实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c=a(bc);
乘法分配律:(a+b)c=ac+bc.
练 4
计算:
(1) +|-6| -22; (2) ()-1 +( -1)0 - ;
(3) -(-1)2 -(π -1)0+2-1.
解:(1)原式=2+6 - 4=4.
(2) 原式=3+1 - 2=2.
(3) 原式=2 -1-1+ = .
例1 用计算器比较-与- 的大小.
解:依次按以下各键: ,
计算器显示的结果为- 2.080 083 823.
依次按以下各键:
,
计算器显示的结果为- 2.080 024 038.
因为- 2.080083 823 < - 2.080 024 038,
所以-< - .
例2 用计算器计算:
(1) +π; (2) 3×- ;
(3) +3-(+ ).
解:(1) 依次按以下各键:
计算器显示的结果为 5.377 660 631,
即 + π ≈5.377 660 631;
解:(2)依次按以下各键:
,
计算器显示的结果为 2.982 719 637,
即3×- ≈2.982 719 637;
(2) 3×- ;
(3) +3-(+ ).
解:+3-(+ ) = +3--
= 3-.
依次按以下各键:
计算器显示的结果为 0.763 932 022 5,
即+3-(+ ) ≈ 0.763 932 0225.
交 流
先通过估算比较下列各组数的大小,再用计算器验证:
(1) -与-1.5;
| - | = ,| -1.5 | = 1.5,
∵()2=3 > 1.52 =2.25,
∴ | - | > | -1.5 | ,
∴ -< - 1.5.
(2) 与0.5.
∵5 >4,
∴ > 2,
∴ > 1,
∴ > ,即 >0.5.
练 习
1. 估算(精确到个位):
(1) ; (2) .
解:(1)∵64<68<72.25,
∴8<<8.5,
∴ ≈8.
解:(2)∵91.125<120<125,
∴4.5<<5,
∴≈5.
2. 用计算器比较下列各组数的大小:
(1) 与; (2) 与;
(3) 与.
<
>
<
3. 用计算器计算:
(1) 3×-2π; (2) -2×+5× ;
(3) -(+ ).
≈ - 2.040 544 62.
≈ 1.827 469 294.
≈ - 1.555 683 434.
阅 读
证明 是无理数
我们可以用下面的方法证明 是无理数:
假设是有理数,那么可以写成 (m、n是正整数,且没有大于1的公约数),即= .
根据平方根的意义,() = 2,即 =2,2n2=m2.
由于上式左边是偶数,所以右边也是偶数,从而可知 m 是偶数.
设 m=2p(p是正整数),
把 m=2p 代入 2n2=m2,得2n2=4p2,即 n2=2p2.
因此,n也是偶数.
于是,m、n 都是 2的倍数,这与 m、n 没有大于1的公约数相矛盾.
因此,= 是不可能的,也就是说不是有理数,它是无理数.
本课小结
实数的性质
1. 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
3. 在进行实数的运算时,有理数的运算法则及运算性
质同样适用.
2. 实数的大小比较方法有:利用数轴比较、利用绝对
值比较、求平方比较、求差比较、求商比较和计
算近似值比较等方法.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
