2023-2024学年苏科版数学八年级上册第1章 全等三角形 小结与思考 课件(共38张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册第1章 全等三角形 小结与思考 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 62.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 18:18:27 | ||
图片预览







文档简介
(共38张PPT)
第1章
全等三角形
小结与思考
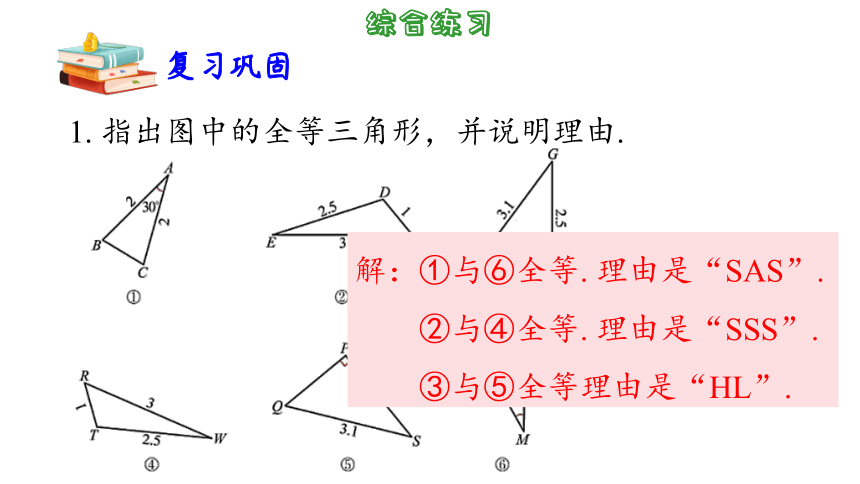
1. 本章知识结构:
全等图形
全等三角形
对应边相等,对应角相等.
两个三角形全等的条件
两个直角三角形全等的条件
斜边、直角边(HL)
边角边(SAS)
角边角(ASA),角角边(AAS)
边边边(SSS)
2. 全等三角形具有“对应边相等,对应角相等”的性质:判定两个三角形全等,通常需要 3 个条件,其中至少要有 1 对边相等,本章中用判定两个三角形全等的基本事实及推论,证明了有关全等三角形的一些命题,证明过程必须言必有据,证明过程的表达必须清晰、简明、有条理,全等三角形的性质与判定有什么关系
3. 本章探索了用直尺和圆规平分已知角、过一点作已知直线的垂线,你能说明这些作图的道理吗
4. 确认图形的性质,通常运用推理的方法,有时也可以运用图形运动的方法. 本章中,我们通过图形的运动探索并确认了一些图形的性质.
5. 举例说明三角形全等在生活中的应用.
复习题
复习巩固
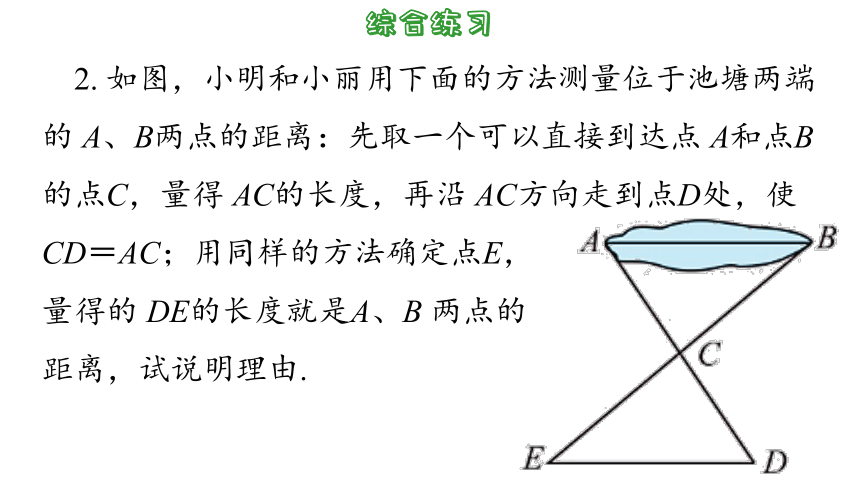
1. 指出图中的全等三角形,并说明理由.
解:①与⑥全等. 理由是“SAS”.
②与④全等. 理由是“SSS”.
③与⑤全等理由是“HL”.
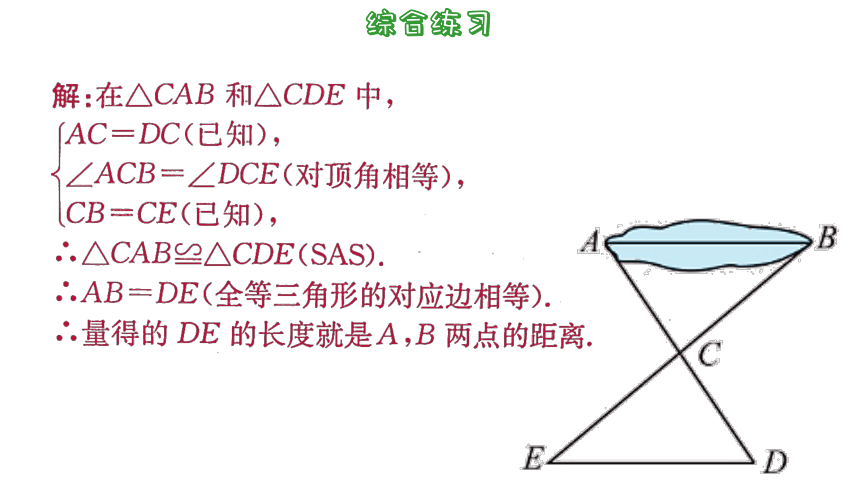
2. 如图,小明和小丽用下面的方法测量位于池塘两端的 A、B两点的距离:先取一个可以直接到达点 A和点B的点C,量得 AC的长度,再沿 AC方向走到点D处,使 CD=AC;用同样的方法确定点E,
量得的 DE的长度就是A、B 两点的
距离,试说明理由.
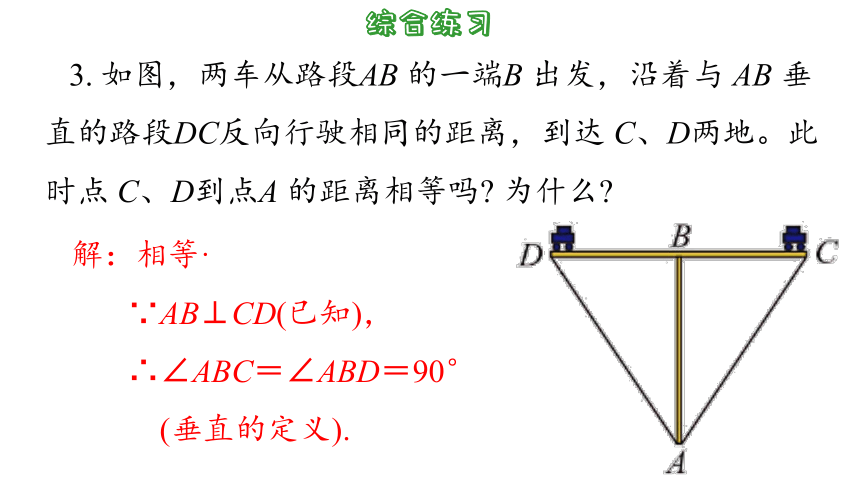
3. 如图,两车从路段AB 的一端B 出发,沿着与 AB 垂直的路段DC反向行驶相同的距离,到达 C、D两地。此时点 C、D到点A 的距离相等吗 为什么
解:相等·
∵AB⊥CD(已知),
∴∠ABC=∠ABD=90°
(垂直的定义).
在△ABC 和△ABD 中,
AB=AB(公共边),
∠ABC=∠ABD(已证)
CB=DB(已知),∴△ABC≌△ABD(SAS).
∴AC=AD
(全等三角形的对应边相等).
4. 已知:如图,在△ABC中,AB=AC,BE、CD是中线.
求证:BE=CD.
证明:∵BE,CD 是中线(已知),
∴AD=AB,AE=AC
(三角形中线的定义).
∵AB=AC (已知),
∴AD=AE (等量代换).
在△ABE 和△ACD 中,
AE=AD(已证),
∠A=∠A(公共角),
AB=AC (已知),
∴△ABE≌△ACD(SAS).
∴BE=CD
(全等三角形的对应边相等).
5. 已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分
别为S、N、Q,且MS=PS.
求证:△MNS ≌ △SQP.
证明:∵MS⊥PS (已知),
∴∠MSN+∠PSQ=90°.
∵MN⊥SN(已知),
∴∠N=90°(垂直的定义).
∴∠M+∠MSN=90° (直角三角形的两个锐角互余).
∴∠M=∠PSQ (同角的余角相等).
∵SN⊥PQ (已知),
∴∠SQP=90°(垂直的定义)
∴∠SQP=∠N (等量代换)
在△MNS 和△SQP中,
∴△MNS≌△SQP(AAS)
∠N=∠SQP(已证)
∠M=∠PSQ(已证)
MS=SP(已知),
6. 已知:如图,AB//CD,AB = CD,AD、BC相交于点O,点E、F在AD上,且BE//CF.
求证:BE=CF.
证明:∵AB∥CD,BE∥CF(已知),
∴∠A=∠D,∠BEO=∠CFO
(两直线平行,内错角相等).
∴∠AEB=∠DFC(等角的补角相等).
在△ABE 和△DCF 中,
∠AEB=∠DFC (已证),
∠A=∠D (已证),
AB=DC (已知),
∴△ABE≌△DCF(AAS).
∴BE=CF
(全等三角形的对应边相等).
7. 已知:如图,AB=DC,AC =DB,AC、DB相交于点O.
求证: △AOB ≌ △DOC.
证明:在△ABC 和△DCB 中,
AB=DC(已知),
AC=DB(已知),
BC=CB(公共边),
∴△ABC≌△DCB(SSS)
∴∠BAC=∠CDB
(全等三角形的对应角相等).
在△AOB 和△DOC 中,
∠AOB=∠DOC(对顶角相等),
∠BAO=∠CDO (已证),
AB=DC(已知),∴△AOB≌△DOC(AAS).
8. 已知:如图,△AOD ≌ △BOC.
求证: △AOC ≌ △BOD.
证明:∵△AOD≌△BOC(已知),
∴ OA=OB,OD=OC
(全等三角形的对应边相等),
∠AOD=∠BOC (全等三角形的对应角相等).
∴∠AOD-∠COD=∠BOC-∠COD (等式的性质),
即∠AOC=∠BOD.
在△AOC 和△BOD 中,
OA=OB(已证),
∠AOC=∠BOD(已证),
OC=OD(已证),
∴△AOC≌△BOD(SAS)
灵活运用
9. 如图,∠A=∠D=90°,AB=DC,AC、BD相交于
点E,找出图中相等的锐角,并加以证明 .
10. 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、
CD 相交于点O. 如果 AB=AC,那么图中有几对全
等的直角三角形 试证明你的结论.
解:有3对全等的直角三角形:
Rt△ABE≌Rt△ACD,
Rt△AOD≌Rt△AOE,
Rt△BOD≌Rt△COE.
11. 如图,AC⊥BC,DC⊥EC,AC=BC, DC=EC. 图中AE、BD 有怎样的数量关系和位置关系 试证明你的结论.
探索研究
12. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,试在方格纸上按下列要求画格点三角形:
(1) 所画的三角形与△ABC全等且有1个公共顶点 C;
E
D
△EDC 如图所示.
(2) 所画的三角形与△ABC全等且有1条公共边 AB.
G
△ABG所图所示(答案不唯一)
13. 在图中沿正方形的网格线把这个图形分割成两个全等形,你有几种不同的分割方法
解:如图所示,有三种分法.
14. 你能用刻度尺画一个已知角的平分线吗 画出图形,并说明画法的道理.
解:能.
作法一:如图所示,
(1)在 OA 上截取 OC=a cm,在OB 上截取OD=a cm.
(2)连接CD,量出CD=b cm,在CD上截取CE=CD=b cm.
(3) 作射线 OE. OE 即为∠AOB 的平分线.
在△OCE 和△ODE 中,
OC=OD (由作法知),
CE=DE (由作法知)
OE=OE (公共边),
∴△OCE ≌ △ODE(SSS).
∴∠COE = ∠DOE,即OE 是∠AOB 的平分线.
作法二:如图所示,
(1) 在∠MON 的两边上分别任取OA=OB,OC=OD.
(2) 连接 AD,BC,相交于点 P. 射线OP就是∠MON的平分线根据.
“SAS”先证明△AOD ≌ △BOC,得∠OAD=∠OBC,
然后根据“AAS”证明 △APC≌△BPD,得AP=BP,
最后根据“SSS”证明 △AOP≌△BOP,得∠AOP=∠BOP,
所以 OP 是∠MON 的平分线.
第1章
全等三角形
小结与思考
1. 本章知识结构:
全等图形
全等三角形
对应边相等,对应角相等.
两个三角形全等的条件
两个直角三角形全等的条件
斜边、直角边(HL)
边角边(SAS)
角边角(ASA),角角边(AAS)
边边边(SSS)
2. 全等三角形具有“对应边相等,对应角相等”的性质:判定两个三角形全等,通常需要 3 个条件,其中至少要有 1 对边相等,本章中用判定两个三角形全等的基本事实及推论,证明了有关全等三角形的一些命题,证明过程必须言必有据,证明过程的表达必须清晰、简明、有条理,全等三角形的性质与判定有什么关系
3. 本章探索了用直尺和圆规平分已知角、过一点作已知直线的垂线,你能说明这些作图的道理吗
4. 确认图形的性质,通常运用推理的方法,有时也可以运用图形运动的方法. 本章中,我们通过图形的运动探索并确认了一些图形的性质.
5. 举例说明三角形全等在生活中的应用.
复习题
复习巩固
1. 指出图中的全等三角形,并说明理由.
解:①与⑥全等. 理由是“SAS”.
②与④全等. 理由是“SSS”.
③与⑤全等理由是“HL”.
2. 如图,小明和小丽用下面的方法测量位于池塘两端的 A、B两点的距离:先取一个可以直接到达点 A和点B的点C,量得 AC的长度,再沿 AC方向走到点D处,使 CD=AC;用同样的方法确定点E,
量得的 DE的长度就是A、B 两点的
距离,试说明理由.
3. 如图,两车从路段AB 的一端B 出发,沿着与 AB 垂直的路段DC反向行驶相同的距离,到达 C、D两地。此时点 C、D到点A 的距离相等吗 为什么
解:相等·
∵AB⊥CD(已知),
∴∠ABC=∠ABD=90°
(垂直的定义).
在△ABC 和△ABD 中,
AB=AB(公共边),
∠ABC=∠ABD(已证)
CB=DB(已知),∴△ABC≌△ABD(SAS).
∴AC=AD
(全等三角形的对应边相等).
4. 已知:如图,在△ABC中,AB=AC,BE、CD是中线.
求证:BE=CD.
证明:∵BE,CD 是中线(已知),
∴AD=AB,AE=AC
(三角形中线的定义).
∵AB=AC (已知),
∴AD=AE (等量代换).
在△ABE 和△ACD 中,
AE=AD(已证),
∠A=∠A(公共角),
AB=AC (已知),
∴△ABE≌△ACD(SAS).
∴BE=CD
(全等三角形的对应边相等).
5. 已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分
别为S、N、Q,且MS=PS.
求证:△MNS ≌ △SQP.
证明:∵MS⊥PS (已知),
∴∠MSN+∠PSQ=90°.
∵MN⊥SN(已知),
∴∠N=90°(垂直的定义).
∴∠M+∠MSN=90° (直角三角形的两个锐角互余).
∴∠M=∠PSQ (同角的余角相等).
∵SN⊥PQ (已知),
∴∠SQP=90°(垂直的定义)
∴∠SQP=∠N (等量代换)
在△MNS 和△SQP中,
∴△MNS≌△SQP(AAS)
∠N=∠SQP(已证)
∠M=∠PSQ(已证)
MS=SP(已知),
6. 已知:如图,AB//CD,AB = CD,AD、BC相交于点O,点E、F在AD上,且BE//CF.
求证:BE=CF.
证明:∵AB∥CD,BE∥CF(已知),
∴∠A=∠D,∠BEO=∠CFO
(两直线平行,内错角相等).
∴∠AEB=∠DFC(等角的补角相等).
在△ABE 和△DCF 中,
∠AEB=∠DFC (已证),
∠A=∠D (已证),
AB=DC (已知),
∴△ABE≌△DCF(AAS).
∴BE=CF
(全等三角形的对应边相等).
7. 已知:如图,AB=DC,AC =DB,AC、DB相交于点O.
求证: △AOB ≌ △DOC.
证明:在△ABC 和△DCB 中,
AB=DC(已知),
AC=DB(已知),
BC=CB(公共边),
∴△ABC≌△DCB(SSS)
∴∠BAC=∠CDB
(全等三角形的对应角相等).
在△AOB 和△DOC 中,
∠AOB=∠DOC(对顶角相等),
∠BAO=∠CDO (已证),
AB=DC(已知),∴△AOB≌△DOC(AAS).
8. 已知:如图,△AOD ≌ △BOC.
求证: △AOC ≌ △BOD.
证明:∵△AOD≌△BOC(已知),
∴ OA=OB,OD=OC
(全等三角形的对应边相等),
∠AOD=∠BOC (全等三角形的对应角相等).
∴∠AOD-∠COD=∠BOC-∠COD (等式的性质),
即∠AOC=∠BOD.
在△AOC 和△BOD 中,
OA=OB(已证),
∠AOC=∠BOD(已证),
OC=OD(已证),
∴△AOC≌△BOD(SAS)
灵活运用
9. 如图,∠A=∠D=90°,AB=DC,AC、BD相交于
点E,找出图中相等的锐角,并加以证明 .
10. 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、
CD 相交于点O. 如果 AB=AC,那么图中有几对全
等的直角三角形 试证明你的结论.
解:有3对全等的直角三角形:
Rt△ABE≌Rt△ACD,
Rt△AOD≌Rt△AOE,
Rt△BOD≌Rt△COE.
11. 如图,AC⊥BC,DC⊥EC,AC=BC, DC=EC. 图中AE、BD 有怎样的数量关系和位置关系 试证明你的结论.
探索研究
12. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,试在方格纸上按下列要求画格点三角形:
(1) 所画的三角形与△ABC全等且有1个公共顶点 C;
E
D
△EDC 如图所示.
(2) 所画的三角形与△ABC全等且有1条公共边 AB.
G
△ABG所图所示(答案不唯一)
13. 在图中沿正方形的网格线把这个图形分割成两个全等形,你有几种不同的分割方法
解:如图所示,有三种分法.
14. 你能用刻度尺画一个已知角的平分线吗 画出图形,并说明画法的道理.
解:能.
作法一:如图所示,
(1)在 OA 上截取 OC=a cm,在OB 上截取OD=a cm.
(2)连接CD,量出CD=b cm,在CD上截取CE=CD=b cm.
(3) 作射线 OE. OE 即为∠AOB 的平分线.
在△OCE 和△ODE 中,
OC=OD (由作法知),
CE=DE (由作法知)
OE=OE (公共边),
∴△OCE ≌ △ODE(SSS).
∴∠COE = ∠DOE,即OE 是∠AOB 的平分线.
作法二:如图所示,
(1) 在∠MON 的两边上分别任取OA=OB,OC=OD.
(2) 连接 AD,BC,相交于点 P. 射线OP就是∠MON的平分线根据.
“SAS”先证明△AOD ≌ △BOC,得∠OAD=∠OBC,
然后根据“AAS”证明 △APC≌△BPD,得AP=BP,
最后根据“SSS”证明 △AOP≌△BOP,得∠AOP=∠BOP,
所以 OP 是∠MON 的平分线.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
