2023-2024学年苏科版数学八年级上册第2章 轴对称图形 小结与思考 课件(共56张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册第2章 轴对称图形 小结与思考 课件(共56张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 62.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 18:19:25 | ||
图片预览










文档简介
(共56张PPT)
第2章
轴对称图形
小结与思考
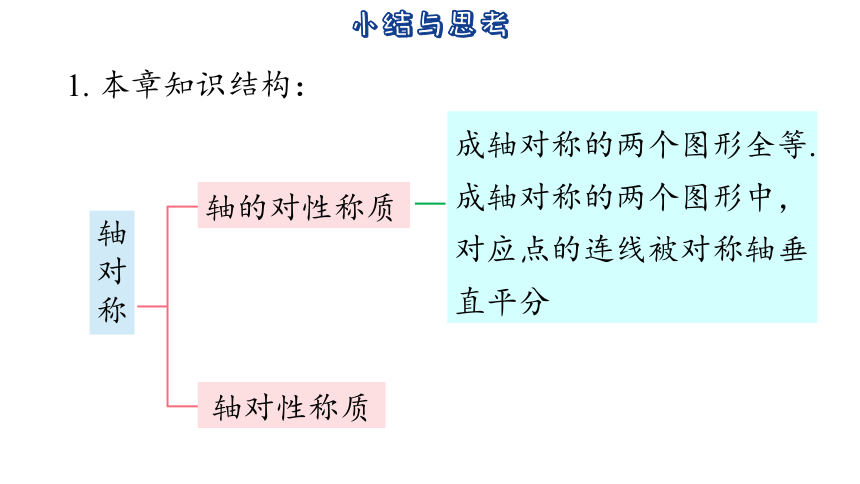
1. 本章知识结构:
轴对称
轴的对性称质
轴对性称质
成轴对称的两个图形全等. 成轴对称的两个图形中,对应点的连线被对称轴垂直平分
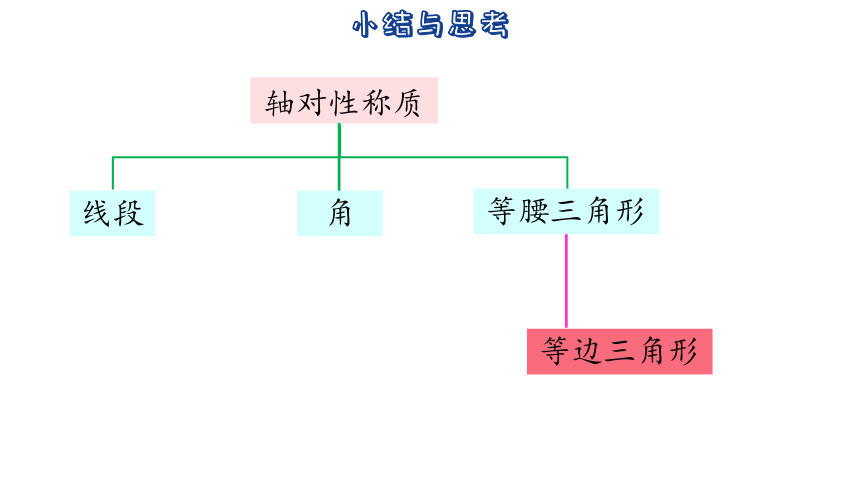
轴对性称质
线段
角
等腰三角形
等边三角形
线段
线段的垂直平分线是它的对称轴
线段垂直平分线上的点到线段两端的距离相等
到线段两端距离相等的点在线段的垂直平分线上
角
角平分线所在直线是它的对称轴
角平分线上的点到角 两边的离相等
角的内部到角两边距离相等的点在角的平分线上
等腰三角形
顶角平分线所在直线是它的对称轴
等腰三角形的两底角相等。等腰三角形底边上的高线、中线及顶角平分线重合
有两个角相等的三角形是等腰三角形
直角三角形斜边上的中线等于斜边的一半
等边三角形
角平分线所在直线它的对称轴
等边三角形的各角都等于 60°
三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形
2. 说说轴对称与轴对称图形的区别和联系.
3.“等腰三角形的两底角相等”揭示了等腰三角形具有的一个性质,称为等腰三角形的性质定理;“有两个角相等的三角形是等腰三角形”揭示了具备什么条件的三角形是等腰三角形,称为等腰三角形的判定定理. 这两个定理是互逆定理.
你能在学过的定理中,再说出一对互逆定理,并指出其中哪一个是性质定理,哪一个是判定定理吗
4. 在本章学习中,通过图形的翻折,探索并证实了线段的垂直平分线、角平分线、等腰三角形的性质. 运用图形运动的方法,也可以研究图形的性质.
5. 本章例题中的“思考与表述”,体现了“由未知想须知”的思路,这是我们探索解决问题途径常用的一种思考方法.
复习题
复习巩固
1.下列图形是不是轴对称图形 如果是,画出它的对称轴.
解:图③不是轴对称图形,图①②④是轴对称图形,画对称轴略.
2. 请查找一些国家的国旗图案,并指出其中哪些是轴对
称图形 试分别找出它们的对称轴.
略
3. (1) 图①是轴对称图形吗 如果是,它有几条对称轴
如果不是可以怎样把它补成轴对称图形
①
解:图①不是轴对称图形,只要把拐角处“断开”部分连接起来,即可补成轴对称图形,如图所示.
(2) 图②由5张全等的正方形纸片组成,只移动其中1张
纸片,你能使它变成轴对称图形吗
②
能,如图所示. (答案不唯一)
4. 如图,在△ABC中,AB= AC,
D是BC的中点,AC 的垂直平
分线分别交 AC、AD、AB 于
点E、F、G. 点F到△ABC的边
__________的距离相等,点F
到△ABC的顶点___________
的距离相等.
AB,AC
A,B,C
5. (1) 在等腰三角形ABC中,∠A=80°.
若∠A是顶角,则∠B= _________°;
若∠B是顶角,则∠B= _________°;
若∠C是顶角,则∠B= _________°.
50
20
80
(2) 等腰三角形ABC的周长为8 cm,AB=3cm.
若AB是底边,则BC= ________ cm;
若_________,则BC =________ cm;
若_________ ,则BC= ________cm.
2.5
BC是底边
2
AC是底边
3
6. 在如图的网格中:
(1)画△A1B1C1,使它与△ABC 关于l1对称;
(2)画△A2B2C2,使它与△A1B1C1关于l2对称;
(3) 画△A3B3C3,使它与△A2B2C2关于l3对称;
(4) 画出△A3B3C3与△ABC 的对称轴.
解:(1)(2)(3)画图如图所示;
(4) 如图中经过点 A,A1,的直线l4 为△A3B3C3与△ABC的对称轴.
7. 根据下列已知条件,分别指出各个图形中的等腰三
角形,并加以证明,
(1) 如图①,BD平分∠ABC,点
E 在BC 上,且 DE∥AB;
解:△BED是等腰三角形.
证明如下:∵BD 平分∠ABC,
∴∠ABD=∠CBD.
∵DE∥AB,
∴∠BDE=∠ABD.
∴∠CBD=∠BDE,
∴EB=ED(等角对等边),
∴△BED 是等腰三角形.
(2) 如图②,AD平分∠BAC,点E在BA的
延长线上,且 EC//AD;
解:△ACE 是等腰三角形.证明如下:
∵AD 平分∠BAC,
∴∠BAD = ∠CAD.
∵EC∥AD,
∴∠BAD =∠E,
∠CAD =∠ACE.
∴∠E=∠ACE,
∴AC=AE (等角对等边),
∴△ACE 是等腰三角形.
(3) 如图③,AD平分∠BAC,点E在
BD 上,点G在CA 的延长线上,
且GE∥AD,GE交AB 于点F.
解:△AGF是等腰三角形.证明如下:
∵AD 平分∠BAC,
∴∠BAD=∠CAD.
∵GE∥AD,
∴∠G=∠CAD,∠AFG=∠BAD.
∴∠G=∠AFG,
∴ AG=AF(等角对等边),
∴△AGF 为等腰三角形.
8. 已知:如图,在△ABC 中,∠ABC、∠ACB的平分线
相交于点O,MN 过点O,且 MN ∥BC,分别
交AB、AC 于点M、N.
求证:MN=BM+CN.
证明:∵BO 平分∠ABC,
∴∠MBO=∠CBO.
∵MN∥BC,
∴∠MOB=∠CBO.
∴∠MBO=∠MOB,
∴BM=MO(等角对等边).
同理 CN=NO.
∴MN=MO+NO=BM+CN.
灵活运用
9. 如图,点 D、E 在 BC 上,且AB=AC,AD=AE. 图中
还有哪些相等的线段 试用不同的方法证明你的结论。
解:BD=CE,BE=CD.
方法一:
∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED.
又∵ ∠ADE=∠B+∠BAD,∠AED=∠C+∠EAC,
∴∠BAD=∠EAC.
在△ABD 和△ACE中,
AB=AC,
∵ ∠BAE=∠CAD,
AE=AD.
∴△BAE≌△CAD(SAS).
∴BE=CD.
∴BE-DE=CD-DE. 即 BD=CE.
10. 已知:如图,∠ABC =∠ADC=90°,M、N 分别
是 AC、BD 的中点.
求证:MN⊥BD.
证明:如图,连接 BM,DM.
11. (1) 野营活动中,小明用一块等腰三角形的铁皮代替
锅,烙一块与铁皮形状、大小相同的饼,烙好一
面后把饼翻身,这块饼仍能正好落在“锅”中,
这是为什么
解:因为烙的饼与“锅(铁皮)”是全等的等腰三角形,而等腰三角形是轴对称图形,所以把饼翻身后会正好落在“锅”中.
(2) 小丽用如图①的直角三角形铁皮,烙一块与铁皮形状、大小相同的饼,如果烙好一面后就把饼翻身,那么这块饼不能正好落在“锅”中. 小丽将饼切了一刀,然后将两小块都翻身,结果饼就能正好落在“锅”中.
小丽怎样切的 为什么
解:小丽将其沿直角三角形斜边中线分开为两个三角形,这两个三角形都是等腰三角形,如图所示的△ACD与△BCD,因此由(1)知“翻身后能与原图形重合,故还是能正好落在“锅”中.
(3) 如果用来烙饼的铁皮既不是等腰三角形也不是直角三角形 (如图②),那么烙好一面后,怎样将烙饼翻身,才能使烙饼仍能正好落在“锅”中
解:如图所示,作△ABC 的高AD,把△ABC 分成两个直角三角形,根据(2)中的方法,再作边AB,AC 的中线DE,DF. 因此,共切3刀:AD,DE,DF,或者只切2刀,即只要找出图中的 D点所在的位置,只需切 DE,DF,图中四边形AEDF 是轴对称图形,
“翻身”后仍能与原来重合.
12. 在一个三角形中,如果一条边上的中线等于这条边的一半,那么这个三角形是直角三角形吗 证明你的结论.
解:这个三角形是直角三角形.
已知:如图所示,在△ABC 中,
D 为AC 的中点 BD=AC.
求证:△ABC 是直角三角形.
13,如图,AB=AC=AD.
(1) 如果 AD∥BC,那么∠C和∠D有
怎样的数量关系 证明你的结论;
解:∠C=2∠D.证明如下:
∵AD∥BC,
∴∠DBC=∠D.
∵AB=AD,
∴∠D=∠ABD,
∴∠ABC=2∠D.
∵AB=AC,
∴∠ABC=∠C.
∴∠C=2∠D.
(2) 如果∠C=2∠D,那么你能得到
什么结论 证明你的结论
解:AD∥BC. 证明如下:
∵AB=AC,
∴∠C=∠ABC=2∠D.
∵AB=AD,
∴∠ABD=∠D.
∵∠ABC=2∠D.
∴∠CBD=∠D.
∴AD∥BC.
探索研究
14. (1) 如图,在△ABC中,∠BAC=90°,AB=AC,
点D在 BC 上且BD=BA,点E在BC的延长线上,
且CE=CA,求∠DAE的度数;
解:在 △ABC 中,
∵∠BAC=90°,AB=AC,
∴∠B=∠BCA=45°.
又∵BA=BD,
∴∠BDA=∠BAD=×(180°-45°) =67.5°.
∵∠BCA=45°,CE=CA,
∴∠CAE=∠E=22.5°.
∴∠DAE= ∠BDA-∠E=67.5°-22.5°=45°.
(2) 如果把第(1)题中“AB=AC”的条件舍去,其余条件
不变,那么∠DAE的度数会改变吗
解:∠DAE 的度数不会改变.如图所示.
∵BD=BA,∠BAC=90°,
∴∠4=∠BAD=90°-∠1.
∵CA=CE,
∴∠2=∠E.
又∵∠4=∠1+∠3,
∠3=∠2+∠E,
∴∠3=2∠2,
∴∠4=90°-∠1=∠1+2∠2,
∴2∠1+2∠2=90°,
∴2(∠1+∠2)=90°,
∴∠1+∠2=45°,
∴∠DAE=45°,
∴∠DAE 的度数不会改变.
(3) 如果把第(1)题中“∠BAC=90°”的条件改为
“∠BAC=90°”,其余条件不变,那么∠DAE
与∠BAC 有怎样的数量关系
解:∠BAC 的度数是∠DAE 度数的2倍.如图所示
∵BA=BD,
∴∠BAD=∠4,
∴∠BAC=∠BAD+∠1=∠4+∠1.
又∵∠4=∠1+∠3,CA=CE,
∴∠2=∠E,
∴∠3=2∠2,
∴∠BAC=∠1+∠4
= ∠1+∠1+2∠2
=2(∠1+∠2).
又∵∠DAE=∠1+∠2.
∴∠BAC=2∠DAE.
∴∠BAC 的度数是∠DAE 度数的2倍.
15. 我们知道:如果点P在线段AB 的垂直平分线l上,那
么PA=PB;如果 PA=PB,那么点P在线段AB 的垂直
平分线l上;如果点P不在线段AB 的垂直平分线l上,
那么 PA≠PB. 试证明:如果 PA≠PB,那么点P不在
线段AB的垂直平分线l上.
证明:假设点P在线段AB的垂直平分线上,由线段垂直平分线的性质“线段垂直平分线上的点到线段两端的距离相等”得 PA=PB,这与PA≠PB 相矛盾,所以点 P 不在线段AB 的垂直平分线上.
16. 已知直线l、点A和点B. 试在直线l上确定一点P,使
PA+PB最小.
解:根据点 A,B 与直线的不同位置讨论如下:
(1) 若点 A,B 在直线l的同侧:如图 1,2,3.
若点 A,B 在直线l的异侧:如图 4,5,6.
(2) 如图1,点 A,B到直线的距离不等,作点A关于直线l对称的点A′,连接AB,线段AB与直线l的交点为P,则此时 PA+PB 最小;
如图2,点A,B到直线的距离相等,线段AB的垂直平分线与直线l的交点为 P,则此时PA+PB最小;
如图 3,点A,B 所在直线垂直于直线l,垂足为P,则此时 PA+PB 最小.
如图 4,5,6,线段 AB 与直线的交点为P,则此时PA+PB 最小.
第2章
轴对称图形
小结与思考
1. 本章知识结构:
轴对称
轴的对性称质
轴对性称质
成轴对称的两个图形全等. 成轴对称的两个图形中,对应点的连线被对称轴垂直平分
轴对性称质
线段
角
等腰三角形
等边三角形
线段
线段的垂直平分线是它的对称轴
线段垂直平分线上的点到线段两端的距离相等
到线段两端距离相等的点在线段的垂直平分线上
角
角平分线所在直线是它的对称轴
角平分线上的点到角 两边的离相等
角的内部到角两边距离相等的点在角的平分线上
等腰三角形
顶角平分线所在直线是它的对称轴
等腰三角形的两底角相等。等腰三角形底边上的高线、中线及顶角平分线重合
有两个角相等的三角形是等腰三角形
直角三角形斜边上的中线等于斜边的一半
等边三角形
角平分线所在直线它的对称轴
等边三角形的各角都等于 60°
三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形
2. 说说轴对称与轴对称图形的区别和联系.
3.“等腰三角形的两底角相等”揭示了等腰三角形具有的一个性质,称为等腰三角形的性质定理;“有两个角相等的三角形是等腰三角形”揭示了具备什么条件的三角形是等腰三角形,称为等腰三角形的判定定理. 这两个定理是互逆定理.
你能在学过的定理中,再说出一对互逆定理,并指出其中哪一个是性质定理,哪一个是判定定理吗
4. 在本章学习中,通过图形的翻折,探索并证实了线段的垂直平分线、角平分线、等腰三角形的性质. 运用图形运动的方法,也可以研究图形的性质.
5. 本章例题中的“思考与表述”,体现了“由未知想须知”的思路,这是我们探索解决问题途径常用的一种思考方法.
复习题
复习巩固
1.下列图形是不是轴对称图形 如果是,画出它的对称轴.
解:图③不是轴对称图形,图①②④是轴对称图形,画对称轴略.
2. 请查找一些国家的国旗图案,并指出其中哪些是轴对
称图形 试分别找出它们的对称轴.
略
3. (1) 图①是轴对称图形吗 如果是,它有几条对称轴
如果不是可以怎样把它补成轴对称图形
①
解:图①不是轴对称图形,只要把拐角处“断开”部分连接起来,即可补成轴对称图形,如图所示.
(2) 图②由5张全等的正方形纸片组成,只移动其中1张
纸片,你能使它变成轴对称图形吗
②
能,如图所示. (答案不唯一)
4. 如图,在△ABC中,AB= AC,
D是BC的中点,AC 的垂直平
分线分别交 AC、AD、AB 于
点E、F、G. 点F到△ABC的边
__________的距离相等,点F
到△ABC的顶点___________
的距离相等.
AB,AC
A,B,C
5. (1) 在等腰三角形ABC中,∠A=80°.
若∠A是顶角,则∠B= _________°;
若∠B是顶角,则∠B= _________°;
若∠C是顶角,则∠B= _________°.
50
20
80
(2) 等腰三角形ABC的周长为8 cm,AB=3cm.
若AB是底边,则BC= ________ cm;
若_________,则BC =________ cm;
若_________ ,则BC= ________cm.
2.5
BC是底边
2
AC是底边
3
6. 在如图的网格中:
(1)画△A1B1C1,使它与△ABC 关于l1对称;
(2)画△A2B2C2,使它与△A1B1C1关于l2对称;
(3) 画△A3B3C3,使它与△A2B2C2关于l3对称;
(4) 画出△A3B3C3与△ABC 的对称轴.
解:(1)(2)(3)画图如图所示;
(4) 如图中经过点 A,A1,的直线l4 为△A3B3C3与△ABC的对称轴.
7. 根据下列已知条件,分别指出各个图形中的等腰三
角形,并加以证明,
(1) 如图①,BD平分∠ABC,点
E 在BC 上,且 DE∥AB;
解:△BED是等腰三角形.
证明如下:∵BD 平分∠ABC,
∴∠ABD=∠CBD.
∵DE∥AB,
∴∠BDE=∠ABD.
∴∠CBD=∠BDE,
∴EB=ED(等角对等边),
∴△BED 是等腰三角形.
(2) 如图②,AD平分∠BAC,点E在BA的
延长线上,且 EC//AD;
解:△ACE 是等腰三角形.证明如下:
∵AD 平分∠BAC,
∴∠BAD = ∠CAD.
∵EC∥AD,
∴∠BAD =∠E,
∠CAD =∠ACE.
∴∠E=∠ACE,
∴AC=AE (等角对等边),
∴△ACE 是等腰三角形.
(3) 如图③,AD平分∠BAC,点E在
BD 上,点G在CA 的延长线上,
且GE∥AD,GE交AB 于点F.
解:△AGF是等腰三角形.证明如下:
∵AD 平分∠BAC,
∴∠BAD=∠CAD.
∵GE∥AD,
∴∠G=∠CAD,∠AFG=∠BAD.
∴∠G=∠AFG,
∴ AG=AF(等角对等边),
∴△AGF 为等腰三角形.
8. 已知:如图,在△ABC 中,∠ABC、∠ACB的平分线
相交于点O,MN 过点O,且 MN ∥BC,分别
交AB、AC 于点M、N.
求证:MN=BM+CN.
证明:∵BO 平分∠ABC,
∴∠MBO=∠CBO.
∵MN∥BC,
∴∠MOB=∠CBO.
∴∠MBO=∠MOB,
∴BM=MO(等角对等边).
同理 CN=NO.
∴MN=MO+NO=BM+CN.
灵活运用
9. 如图,点 D、E 在 BC 上,且AB=AC,AD=AE. 图中
还有哪些相等的线段 试用不同的方法证明你的结论。
解:BD=CE,BE=CD.
方法一:
∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED.
又∵ ∠ADE=∠B+∠BAD,∠AED=∠C+∠EAC,
∴∠BAD=∠EAC.
在△ABD 和△ACE中,
AB=AC,
∵ ∠BAE=∠CAD,
AE=AD.
∴△BAE≌△CAD(SAS).
∴BE=CD.
∴BE-DE=CD-DE. 即 BD=CE.
10. 已知:如图,∠ABC =∠ADC=90°,M、N 分别
是 AC、BD 的中点.
求证:MN⊥BD.
证明:如图,连接 BM,DM.
11. (1) 野营活动中,小明用一块等腰三角形的铁皮代替
锅,烙一块与铁皮形状、大小相同的饼,烙好一
面后把饼翻身,这块饼仍能正好落在“锅”中,
这是为什么
解:因为烙的饼与“锅(铁皮)”是全等的等腰三角形,而等腰三角形是轴对称图形,所以把饼翻身后会正好落在“锅”中.
(2) 小丽用如图①的直角三角形铁皮,烙一块与铁皮形状、大小相同的饼,如果烙好一面后就把饼翻身,那么这块饼不能正好落在“锅”中. 小丽将饼切了一刀,然后将两小块都翻身,结果饼就能正好落在“锅”中.
小丽怎样切的 为什么
解:小丽将其沿直角三角形斜边中线分开为两个三角形,这两个三角形都是等腰三角形,如图所示的△ACD与△BCD,因此由(1)知“翻身后能与原图形重合,故还是能正好落在“锅”中.
(3) 如果用来烙饼的铁皮既不是等腰三角形也不是直角三角形 (如图②),那么烙好一面后,怎样将烙饼翻身,才能使烙饼仍能正好落在“锅”中
解:如图所示,作△ABC 的高AD,把△ABC 分成两个直角三角形,根据(2)中的方法,再作边AB,AC 的中线DE,DF. 因此,共切3刀:AD,DE,DF,或者只切2刀,即只要找出图中的 D点所在的位置,只需切 DE,DF,图中四边形AEDF 是轴对称图形,
“翻身”后仍能与原来重合.
12. 在一个三角形中,如果一条边上的中线等于这条边的一半,那么这个三角形是直角三角形吗 证明你的结论.
解:这个三角形是直角三角形.
已知:如图所示,在△ABC 中,
D 为AC 的中点 BD=AC.
求证:△ABC 是直角三角形.
13,如图,AB=AC=AD.
(1) 如果 AD∥BC,那么∠C和∠D有
怎样的数量关系 证明你的结论;
解:∠C=2∠D.证明如下:
∵AD∥BC,
∴∠DBC=∠D.
∵AB=AD,
∴∠D=∠ABD,
∴∠ABC=2∠D.
∵AB=AC,
∴∠ABC=∠C.
∴∠C=2∠D.
(2) 如果∠C=2∠D,那么你能得到
什么结论 证明你的结论
解:AD∥BC. 证明如下:
∵AB=AC,
∴∠C=∠ABC=2∠D.
∵AB=AD,
∴∠ABD=∠D.
∵∠ABC=2∠D.
∴∠CBD=∠D.
∴AD∥BC.
探索研究
14. (1) 如图,在△ABC中,∠BAC=90°,AB=AC,
点D在 BC 上且BD=BA,点E在BC的延长线上,
且CE=CA,求∠DAE的度数;
解:在 △ABC 中,
∵∠BAC=90°,AB=AC,
∴∠B=∠BCA=45°.
又∵BA=BD,
∴∠BDA=∠BAD=×(180°-45°) =67.5°.
∵∠BCA=45°,CE=CA,
∴∠CAE=∠E=22.5°.
∴∠DAE= ∠BDA-∠E=67.5°-22.5°=45°.
(2) 如果把第(1)题中“AB=AC”的条件舍去,其余条件
不变,那么∠DAE的度数会改变吗
解:∠DAE 的度数不会改变.如图所示.
∵BD=BA,∠BAC=90°,
∴∠4=∠BAD=90°-∠1.
∵CA=CE,
∴∠2=∠E.
又∵∠4=∠1+∠3,
∠3=∠2+∠E,
∴∠3=2∠2,
∴∠4=90°-∠1=∠1+2∠2,
∴2∠1+2∠2=90°,
∴2(∠1+∠2)=90°,
∴∠1+∠2=45°,
∴∠DAE=45°,
∴∠DAE 的度数不会改变.
(3) 如果把第(1)题中“∠BAC=90°”的条件改为
“∠BAC=90°”,其余条件不变,那么∠DAE
与∠BAC 有怎样的数量关系
解:∠BAC 的度数是∠DAE 度数的2倍.如图所示
∵BA=BD,
∴∠BAD=∠4,
∴∠BAC=∠BAD+∠1=∠4+∠1.
又∵∠4=∠1+∠3,CA=CE,
∴∠2=∠E,
∴∠3=2∠2,
∴∠BAC=∠1+∠4
= ∠1+∠1+2∠2
=2(∠1+∠2).
又∵∠DAE=∠1+∠2.
∴∠BAC=2∠DAE.
∴∠BAC 的度数是∠DAE 度数的2倍.
15. 我们知道:如果点P在线段AB 的垂直平分线l上,那
么PA=PB;如果 PA=PB,那么点P在线段AB 的垂直
平分线l上;如果点P不在线段AB 的垂直平分线l上,
那么 PA≠PB. 试证明:如果 PA≠PB,那么点P不在
线段AB的垂直平分线l上.
证明:假设点P在线段AB的垂直平分线上,由线段垂直平分线的性质“线段垂直平分线上的点到线段两端的距离相等”得 PA=PB,这与PA≠PB 相矛盾,所以点 P 不在线段AB 的垂直平分线上.
16. 已知直线l、点A和点B. 试在直线l上确定一点P,使
PA+PB最小.
解:根据点 A,B 与直线的不同位置讨论如下:
(1) 若点 A,B 在直线l的同侧:如图 1,2,3.
若点 A,B 在直线l的异侧:如图 4,5,6.
(2) 如图1,点 A,B到直线的距离不等,作点A关于直线l对称的点A′,连接AB,线段AB与直线l的交点为P,则此时 PA+PB 最小;
如图2,点A,B到直线的距离相等,线段AB的垂直平分线与直线l的交点为 P,则此时PA+PB最小;
如图 3,点A,B 所在直线垂直于直线l,垂足为P,则此时 PA+PB 最小.
如图 4,5,6,线段 AB 与直线的交点为P,则此时PA+PB 最小.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
