2023-2024学年苏科版数学八年级上册第5章 平面直角坐标系 小结与思考 课件(共23张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册第5章 平面直角坐标系 小结与思考 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 59.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 18:21:38 | ||
图片预览







文档简介
(共23张PPT)
第5章
平面直角坐标系
小结与思考
1. 平面直角坐标系的两条坐标轴互相垂直且有公共原点,两条坐标轴的单位长度通常相等。根据实际问题的需要,两条坐标轴的单位长度也可以不相等.
2. 在平面直角坐标系中,一对有序实数可以确定一个点的位置,一个点的位置也可以用一对有序实数来表示,这样就建立了数量变化与位置变化之间的联系.
3. 平面直角坐标系把坐标平面分为 4 个象限:第一象限、第二象限、第三象限、第四象限.
坐标轴不属于任何象限.
第一、二、三、四象限内点的坐标符号分别是
(+,+)、(-,+)、(-, -) 、(+ , -).
x 轴上点的横坐标为任意实数,纵坐标为 0;
y 轴上点的横坐标为 0,纵坐标为任意实数.
4. 坐标平面内任意一点 P(a,b)关于 a 轴、y 轴、原点对称的点分别是点:
P1(a, -b)、P2(-a,b)、P3(-a, -b).
5. 在探究有关实际问题时,常常通过建立恰当的平面直角坐标系,就可以用较为简明的坐标描述物体的位置、刻画一个图形,从而便于我们研究和解决问题.
6. 举例说明平面直角坐标系在日常生活中的应用.
复习题
复习巩固
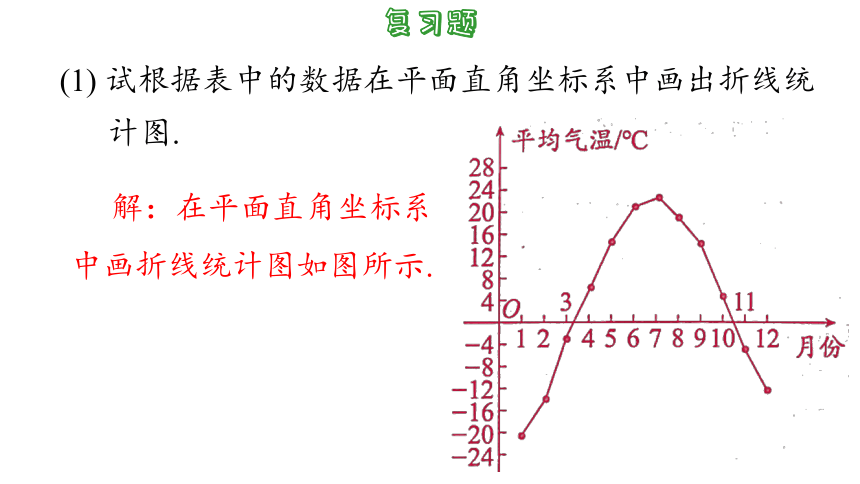
1. 某地某年的月平均气温(℃)如下:
(1) 试根据表中的数据在平面直角坐标系中画出折线统
计图.
(2) 哪几个月的平均气温逐渐上升
(3)哪几个月的平均气温逐渐下降
(1) 试根据表中的数据在平面直角坐标系中画出折线统
计图.
解:在平面直角坐标系中画折线统计图如图所示.
(2) 哪几个月的平均气温逐渐上升
(3)哪几个月的平均气温逐渐下降
1月~7月的平均气温逐渐上升.
7月~12月的平均气温逐渐下降.
2. 根据下列各组点的坐标,在平面直角坐标系中分别
画出下列各组点,以这些点为顶点的图形分别是什
么图形
(1) A(2,1),B(4,1),C(4,5);
(2) A(3,4),B(-3,4),C(0,-2);
(3) A(1,0),B(0,1),C(-1,0),D(0,-1);
(4) A(-2,3),B(3,4),C(3,-4),D(-2,-5).
解:分别画图如图所示.
(1)图1是直角三角形.
(2)图2是等腰三角形.
(3)图3是正方形.
(4) 图 4 是平行四边形.
3. 指出下列各点所在象限或坐标轴:
A(-2.5,3.5),B(4,-2),C(10,5),D(-,-), E(0,-).
解:点 A (-2.5,3.5) 在第二象限,
点 B (4,-2) 在第四象限,
点 C (10,5) 在第一家限,
点 D (-,-) 在第三象限,
点 E (0 ,-) 在y 轴的负半轴上.
4. 填表:
点的坐标 (5,2) (-2,5) (-2,-4) (4,-2)
关于 x 轴对称的点的坐标 (5,-2) (-5,-2) (-2,4) (4,2)
关于 y 轴对称的点的坐标 (-5,2) (2,5) (2,-4) (-4,2)
5. 如图,正方形 ABCD
的边长是4,写出它
的 4 个顶点及对角线
交点 E 的坐标.
解:A (-1,-1),
B (3,-1),C(3,3),
D (-1,3),E(1,1).
6. 填空:
(1) 已知点 A(a,-b)、B(-a, -b)、C(-a,b),且
a≠0,b≠0.
其中,关于x轴对称的两点是_______和________;
关于 y 轴对称的两点是________和_________.
(2) 已知点P(1-m,2-n).
如果 m>1、n<2,那么点P在第______象限;
如果 m=1,那么点P在________.
点B
点C
点A
点B
二
y轴上
7. 填表:
点的横坐标(符号) 点的纵坐标(符号) 点所在的象限或坐标轴
+ + 第一象限
- + 第二象限
+ - 第四象限
- - 第三象限
0 0 坐标原点
- 0 x 轴的负半轴
+ 0 x轴的正半轴
0 - y 轴的负半轴
0 + y 轴的正半轴
灵活运用
8. 小明在平面直角坐标系中
画了一幅图案(如图),他
怎样描述这幅图案,可以
使别人根据他的描述能画
出同样的图案
略
9. 已知点A(0,0)、B(3,0),点 C 在 y 轴上,且△ABC
的面积是5. 求点 C 的坐标.
解:由点A(0,0)与 B(3,0)可得AB=3,
由S△ABC =×3·AC=5,解得AC=.
点C 既可以在y轴的正半轴,也可以在y轴的负半轴,
所以点 C 的纵坐标为或-,
所以点C的坐标为(0,)或(0,-)
探索研究
10. 平行四边形的两个顶点的坐标分别为(-3,0)、(1,0),
第 3个顶点在 y 轴上,且与 x 轴的距离为 3 个单位长
度,求第 4 个顶点的坐标,
解:第4 个顶点的坐标有 6 种可能,分别为(4,3),(-4,3),(-2,-3),如图1所示;
(4,-3),(-4,-3),(-2,3),如图2所示.
11. 在平面直角坐标系中,以点 A(-1,2)为一个顶点画
长方形,使它的两边分别与坐标轴平行,且两边长
分别为 3、4. 写出所画长方形的其余三个顶点的坐标.
解:第一种情况如图1所示.
如果和 x轴平行的边的长是4,和y轴平行的边的长是 3,那么其余三个顶点的坐标分别为
①B(3,2),C(3,-1),
D(-1,-1);
②B′(3,2),C′(3,5),
D′(-1,5);
③B″(-5,2),C″(-5,5),D″(-1,5);
④B″′(-5,2),C″′(-5,-1),D″′(-1,-1).
第二种情况如图2所示.
如果和 x 轴平行的边的长是 3,
和y 轴平行的边的长是 4.那么其
余三个顶点的坐标分别为
① B(2,2),C(2,-2),D(-1,-2);
② B′(2,2),C′(2,6),D′(-1,6);
③ B″(-4,2),C″(-4,6),D″(-1,6);
④ B′′′ (-4,2),C′′′ (-4,-2),D′′′ (-1,-2).
第5章
平面直角坐标系
小结与思考
1. 平面直角坐标系的两条坐标轴互相垂直且有公共原点,两条坐标轴的单位长度通常相等。根据实际问题的需要,两条坐标轴的单位长度也可以不相等.
2. 在平面直角坐标系中,一对有序实数可以确定一个点的位置,一个点的位置也可以用一对有序实数来表示,这样就建立了数量变化与位置变化之间的联系.
3. 平面直角坐标系把坐标平面分为 4 个象限:第一象限、第二象限、第三象限、第四象限.
坐标轴不属于任何象限.
第一、二、三、四象限内点的坐标符号分别是
(+,+)、(-,+)、(-, -) 、(+ , -).
x 轴上点的横坐标为任意实数,纵坐标为 0;
y 轴上点的横坐标为 0,纵坐标为任意实数.
4. 坐标平面内任意一点 P(a,b)关于 a 轴、y 轴、原点对称的点分别是点:
P1(a, -b)、P2(-a,b)、P3(-a, -b).
5. 在探究有关实际问题时,常常通过建立恰当的平面直角坐标系,就可以用较为简明的坐标描述物体的位置、刻画一个图形,从而便于我们研究和解决问题.
6. 举例说明平面直角坐标系在日常生活中的应用.
复习题
复习巩固
1. 某地某年的月平均气温(℃)如下:
(1) 试根据表中的数据在平面直角坐标系中画出折线统
计图.
(2) 哪几个月的平均气温逐渐上升
(3)哪几个月的平均气温逐渐下降
(1) 试根据表中的数据在平面直角坐标系中画出折线统
计图.
解:在平面直角坐标系中画折线统计图如图所示.
(2) 哪几个月的平均气温逐渐上升
(3)哪几个月的平均气温逐渐下降
1月~7月的平均气温逐渐上升.
7月~12月的平均气温逐渐下降.
2. 根据下列各组点的坐标,在平面直角坐标系中分别
画出下列各组点,以这些点为顶点的图形分别是什
么图形
(1) A(2,1),B(4,1),C(4,5);
(2) A(3,4),B(-3,4),C(0,-2);
(3) A(1,0),B(0,1),C(-1,0),D(0,-1);
(4) A(-2,3),B(3,4),C(3,-4),D(-2,-5).
解:分别画图如图所示.
(1)图1是直角三角形.
(2)图2是等腰三角形.
(3)图3是正方形.
(4) 图 4 是平行四边形.
3. 指出下列各点所在象限或坐标轴:
A(-2.5,3.5),B(4,-2),C(10,5),D(-,-), E(0,-).
解:点 A (-2.5,3.5) 在第二象限,
点 B (4,-2) 在第四象限,
点 C (10,5) 在第一家限,
点 D (-,-) 在第三象限,
点 E (0 ,-) 在y 轴的负半轴上.
4. 填表:
点的坐标 (5,2) (-2,5) (-2,-4) (4,-2)
关于 x 轴对称的点的坐标 (5,-2) (-5,-2) (-2,4) (4,2)
关于 y 轴对称的点的坐标 (-5,2) (2,5) (2,-4) (-4,2)
5. 如图,正方形 ABCD
的边长是4,写出它
的 4 个顶点及对角线
交点 E 的坐标.
解:A (-1,-1),
B (3,-1),C(3,3),
D (-1,3),E(1,1).
6. 填空:
(1) 已知点 A(a,-b)、B(-a, -b)、C(-a,b),且
a≠0,b≠0.
其中,关于x轴对称的两点是_______和________;
关于 y 轴对称的两点是________和_________.
(2) 已知点P(1-m,2-n).
如果 m>1、n<2,那么点P在第______象限;
如果 m=1,那么点P在________.
点B
点C
点A
点B
二
y轴上
7. 填表:
点的横坐标(符号) 点的纵坐标(符号) 点所在的象限或坐标轴
+ + 第一象限
- + 第二象限
+ - 第四象限
- - 第三象限
0 0 坐标原点
- 0 x 轴的负半轴
+ 0 x轴的正半轴
0 - y 轴的负半轴
0 + y 轴的正半轴
灵活运用
8. 小明在平面直角坐标系中
画了一幅图案(如图),他
怎样描述这幅图案,可以
使别人根据他的描述能画
出同样的图案
略
9. 已知点A(0,0)、B(3,0),点 C 在 y 轴上,且△ABC
的面积是5. 求点 C 的坐标.
解:由点A(0,0)与 B(3,0)可得AB=3,
由S△ABC =×3·AC=5,解得AC=.
点C 既可以在y轴的正半轴,也可以在y轴的负半轴,
所以点 C 的纵坐标为或-,
所以点C的坐标为(0,)或(0,-)
探索研究
10. 平行四边形的两个顶点的坐标分别为(-3,0)、(1,0),
第 3个顶点在 y 轴上,且与 x 轴的距离为 3 个单位长
度,求第 4 个顶点的坐标,
解:第4 个顶点的坐标有 6 种可能,分别为(4,3),(-4,3),(-2,-3),如图1所示;
(4,-3),(-4,-3),(-2,3),如图2所示.
11. 在平面直角坐标系中,以点 A(-1,2)为一个顶点画
长方形,使它的两边分别与坐标轴平行,且两边长
分别为 3、4. 写出所画长方形的其余三个顶点的坐标.
解:第一种情况如图1所示.
如果和 x轴平行的边的长是4,和y轴平行的边的长是 3,那么其余三个顶点的坐标分别为
①B(3,2),C(3,-1),
D(-1,-1);
②B′(3,2),C′(3,5),
D′(-1,5);
③B″(-5,2),C″(-5,5),D″(-1,5);
④B″′(-5,2),C″′(-5,-1),D″′(-1,-1).
第二种情况如图2所示.
如果和 x 轴平行的边的长是 3,
和y 轴平行的边的长是 4.那么其
余三个顶点的坐标分别为
① B(2,2),C(2,-2),D(-1,-2);
② B′(2,2),C′(2,6),D′(-1,6);
③ B″(-4,2),C″(-4,6),D″(-1,6);
④ B′′′ (-4,2),C′′′ (-4,-2),D′′′ (-1,-2).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
