2023-2024学年苏科版数学八年级上册第4章 实数 小结与思考 课件(共32张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册第4章 实数 小结与思考 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 59.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 18:22:48 | ||
图片预览









文档简介
(共32张PPT)
第4章
实 数
小结与思考
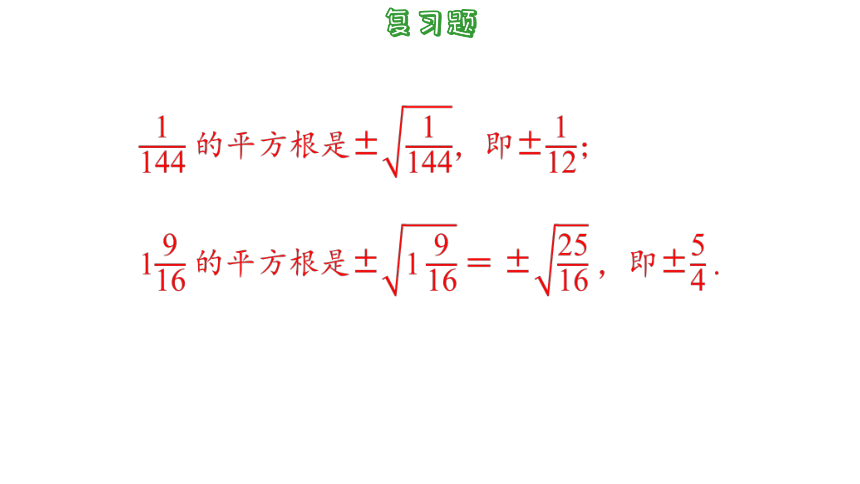
1. 数的概念从有理数扩充到实数.
实数
有理数
正有理数
0
负有理数
无理数
正有理数
负有理数
有限小数或循环小数
无限不循环小数
2. 每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数,实数与数轴上的点一一对应.
3. 开方运算与乘方运算有什么联系 任何实数总可以进行开方运算吗
复习题
复习巩固
1. 在 、、1.732、 、0.、、-、
中,哪些数是无理数?
、、 是无理数.
2. 求下列各数的平方根:
, 6.25, 10, , 1.
解: 的平方根是±,即±;
6.25 的平方根是±,即±2.5;
10的平方根是± ;
的平方根是±,即±;
1 的平方根是± = ± ,即±.
3. 求下列各数的立方根:
-1 000,0.125, -, -5,3.
解:-1 000 的平方根是,即-10;
0.125 的平方根是,即0.5;
- 的平方根是,即;
-5的平方根是,即-;
3 的平方根是 = ,即.
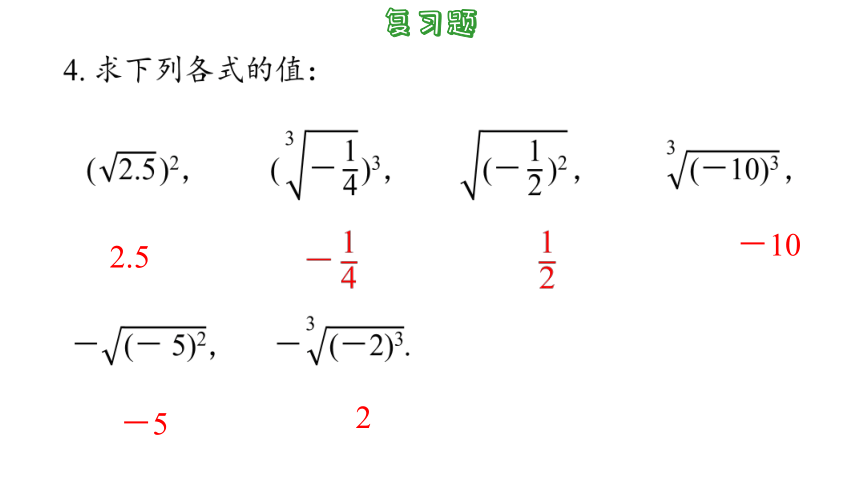
4. 求下列各式的值:
()2, ()3, , ,
-, -.
2.5
-10
-5
2
5. 求下列各式中的 x:
(1) 5x2=10;
(2) x3-2=6;
(3) (2x)2=0.25;
(4) ( x+4 )3=-64.
x=±
x=2
x=±0.25
x=-8
6. 求下列各数的相反数和绝对值:
, -2, -π,2-,1.4-.
解:=- ,它的相反数为,绝对值为.
-2的相反数为2,绝对值为2 .
-π 的相反数为-,绝对值为-.
2- 的相反数为-2,绝对值为2-.
1.4- 的相反数为-1.4,绝对值为-1.4.
7. 用计算器求值(精确到 0.001):
,
,
,
,
.
≈4.743;
≈1.009;
≈0.209;
≈0.476;
≈1.170 .
8. 用计算器计算(精确到 0.01):
(1) 2×-3×5 ;
(2) -+2π-.
1.46
2.59
9. 估算 、 、 、 的值(精确到0.1).
解:∵4.22 = 17.64,4.32 = 18.49,∴ ≈ 4.2.
∵5.82 = 33.64,5.92=34.81,∴≈ 5.8.
∵23 = 8,2.13=9.261,∴≈ 2.1.
∵3.93 = 59.319,43=64,∴≈ 3.9.
10. 比较下列各组数的大小:
(1) 2.0与2.020 020 002···;
(2) - 与 -;
(3) | - | 与 -;
(4) π-3 与 0.14.
2.0 > 2.020 020 002···
- < -
| - | = -
π-3 > 0.14
灵活运用
11. 如图,一艘轮船从甲地向南偏西 45°
方向航行80km 到达乙地,然后又向
北航行 100 km 到达丙地,这时它离
甲地多远(精确到1 km)
D
A
C
B
F
x
45°
解:如图所示,过点A作AD⊥BC,垂足为 D. 设 AD=x km.
D
A
C
B
F
x
45°
由题意,知 BC∥AF,
∴∠DBA=∠BAD=45°,
∴ DB=DA=x.
在Rt△ADB中,由勾股定理,得
AD2+BD2=AB2,即x2+y2=802,
∴ x2=3 200,
x=,
D
A
C
B
F
x
45°
在Rt△ACD中,由勾股定理,得
AC2 = AD2 + DC2
= 3 200 +(100- )2
≈ 3200 + 1886.3
= 5 086.3.
∴ AC≈71 km.
∴轮船到达丙地时离甲地约为 71 km.
12. 如图,长为10m 的梯子AB斜靠在墙上,梯子的顶端
A 到地面的距离AC为8m. 当梯子的顶端 A下滑1m到
点A′时,底端 B向外滑动到点B′,
求BB′的长(精确到0.1m).
如果梯子的顶端下滑 1.5 m,
那么它的底端向外滑动的距离
是多少(精确到0.1m)
解:∵AC⊥BC,AB=10 m,AC=8 m,
∴ BC==6(m).
∵AA′=1m,
∴A′C=8-1=7(m).
在Rt△A′CB′中,
B′C=
= = ≈7.1(m).
∴BB′=B′C-BC≈7.1-6=1.1(m).
如果梯子顶端下滑1.5m,
那么A′C=8-1.5=6.5(m),
∴B′C=
=
= 57.75≈7.6(m).
故 BB′=B′C-BC≈7.6-6 =1.6(m).
13. 如图,点阵中以相邻 4 个点为顶点的小正方形面积
为 1,计算 △ABC 的周长和面积(精确到 0.1).
解:S△ABC=2×4-×1×3 - ×1×4
=8- -1-2 =3.5.
∵AB = = ,AC==,
BC==,
∴ AB+AC+BC = ++ ≈ 9.5.
探索研究
14. 在方格纸上画出面积分别等于 10、17、20 的正方形
(每个小方格的面积为 1).
解:如图所示,正方形ABCD 的面积为10,正方形EFGH的面积为17,正方形MNPQ的面积为20.
15. 把由 5个小正方形组成的十字形纸板(如图)剪开,使
剪成的若干块能够拼成一个大正方形;
(1) 如果剪4刀,应如何剪拼
(2) 最少只需剪几刀
解:(1) 如图1所示,沿虚线剪 4 刀,即可拼成一个大正方形.
(2) 最少只需剪2刀,也能拼成一个大正方形,如图2所示,沿其中的虚线剪2 刀,即可拼成一个大正方形.
本课结束
THANKS!
第4章
实 数
小结与思考
1. 数的概念从有理数扩充到实数.
实数
有理数
正有理数
0
负有理数
无理数
正有理数
负有理数
有限小数或循环小数
无限不循环小数
2. 每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数,实数与数轴上的点一一对应.
3. 开方运算与乘方运算有什么联系 任何实数总可以进行开方运算吗
复习题
复习巩固
1. 在 、、1.732、 、0.、、-、
中,哪些数是无理数?
、、 是无理数.
2. 求下列各数的平方根:
, 6.25, 10, , 1.
解: 的平方根是±,即±;
6.25 的平方根是±,即±2.5;
10的平方根是± ;
的平方根是±,即±;
1 的平方根是± = ± ,即±.
3. 求下列各数的立方根:
-1 000,0.125, -, -5,3.
解:-1 000 的平方根是,即-10;
0.125 的平方根是,即0.5;
- 的平方根是,即;
-5的平方根是,即-;
3 的平方根是 = ,即.
4. 求下列各式的值:
()2, ()3, , ,
-, -.
2.5
-10
-5
2
5. 求下列各式中的 x:
(1) 5x2=10;
(2) x3-2=6;
(3) (2x)2=0.25;
(4) ( x+4 )3=-64.
x=±
x=2
x=±0.25
x=-8
6. 求下列各数的相反数和绝对值:
, -2, -π,2-,1.4-.
解:=- ,它的相反数为,绝对值为.
-2的相反数为2,绝对值为2 .
-π 的相反数为-,绝对值为-.
2- 的相反数为-2,绝对值为2-.
1.4- 的相反数为-1.4,绝对值为-1.4.
7. 用计算器求值(精确到 0.001):
,
,
,
,
.
≈4.743;
≈1.009;
≈0.209;
≈0.476;
≈1.170 .
8. 用计算器计算(精确到 0.01):
(1) 2×-3×5 ;
(2) -+2π-.
1.46
2.59
9. 估算 、 、 、 的值(精确到0.1).
解:∵4.22 = 17.64,4.32 = 18.49,∴ ≈ 4.2.
∵5.82 = 33.64,5.92=34.81,∴≈ 5.8.
∵23 = 8,2.13=9.261,∴≈ 2.1.
∵3.93 = 59.319,43=64,∴≈ 3.9.
10. 比较下列各组数的大小:
(1) 2.0与2.020 020 002···;
(2) - 与 -;
(3) | - | 与 -;
(4) π-3 与 0.14.
2.0 > 2.020 020 002···
- < -
| - | = -
π-3 > 0.14
灵活运用
11. 如图,一艘轮船从甲地向南偏西 45°
方向航行80km 到达乙地,然后又向
北航行 100 km 到达丙地,这时它离
甲地多远(精确到1 km)
D
A
C
B
F
x
45°
解:如图所示,过点A作AD⊥BC,垂足为 D. 设 AD=x km.
D
A
C
B
F
x
45°
由题意,知 BC∥AF,
∴∠DBA=∠BAD=45°,
∴ DB=DA=x.
在Rt△ADB中,由勾股定理,得
AD2+BD2=AB2,即x2+y2=802,
∴ x2=3 200,
x=,
D
A
C
B
F
x
45°
在Rt△ACD中,由勾股定理,得
AC2 = AD2 + DC2
= 3 200 +(100- )2
≈ 3200 + 1886.3
= 5 086.3.
∴ AC≈71 km.
∴轮船到达丙地时离甲地约为 71 km.
12. 如图,长为10m 的梯子AB斜靠在墙上,梯子的顶端
A 到地面的距离AC为8m. 当梯子的顶端 A下滑1m到
点A′时,底端 B向外滑动到点B′,
求BB′的长(精确到0.1m).
如果梯子的顶端下滑 1.5 m,
那么它的底端向外滑动的距离
是多少(精确到0.1m)
解:∵AC⊥BC,AB=10 m,AC=8 m,
∴ BC==6(m).
∵AA′=1m,
∴A′C=8-1=7(m).
在Rt△A′CB′中,
B′C=
= = ≈7.1(m).
∴BB′=B′C-BC≈7.1-6=1.1(m).
如果梯子顶端下滑1.5m,
那么A′C=8-1.5=6.5(m),
∴B′C=
=
= 57.75≈7.6(m).
故 BB′=B′C-BC≈7.6-6 =1.6(m).
13. 如图,点阵中以相邻 4 个点为顶点的小正方形面积
为 1,计算 △ABC 的周长和面积(精确到 0.1).
解:S△ABC=2×4-×1×3 - ×1×4
=8- -1-2 =3.5.
∵AB = = ,AC==,
BC==,
∴ AB+AC+BC = ++ ≈ 9.5.
探索研究
14. 在方格纸上画出面积分别等于 10、17、20 的正方形
(每个小方格的面积为 1).
解:如图所示,正方形ABCD 的面积为10,正方形EFGH的面积为17,正方形MNPQ的面积为20.
15. 把由 5个小正方形组成的十字形纸板(如图)剪开,使
剪成的若干块能够拼成一个大正方形;
(1) 如果剪4刀,应如何剪拼
(2) 最少只需剪几刀
解:(1) 如图1所示,沿虚线剪 4 刀,即可拼成一个大正方形.
(2) 最少只需剪2刀,也能拼成一个大正方形,如图2所示,沿其中的虚线剪2 刀,即可拼成一个大正方形.
本课结束
THANKS!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
