2023-2024学年苏科版数学八年级上册第6章 一次函数 小结与思考 课件(共44张PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册第6章 一次函数 小结与思考 课件(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 60.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 18:23:51 | ||
图片预览











文档简介
(共44张PPT)
第6章
一次函数
小结与思考
1. 在一个变化过程中,往往有许多变化的量,其中的一些变量之间常常有着一定的关系,在本章里,我们研究了某些变化过程中两个变量之间的特殊关系——正比例函数关系和一次函数关系.
2. 变量之间的函数关系通常可以用表格、图像和函数表达式表示,这3种表示法各有什么特点
3. 函数 y=kx+6(其中 k、b 为常数,且 k≠0)称为一次函数,一次函数的图像是一条直线. 确定一次函数表达式通常需要几个条件
正比例函数 y=kx(k 是常数,且 k≠0)是特殊的一次函数,它的图像是经过原点且与一次函数 y=kx+b 的图像平行的一条直线,确定一个正比例函数表达式需要几个条件
4. 二元一次方程与一次函数有什么联系 如何利用一次函数的图像求二元次方程组的解
5. 函数刻画现实世界数量的变化及其关系,方程刻画现实世界数量之间的相等关系,不等式刻画现实世界数量之间的不等关系, 当函数中的一个变量的值确定时,可由相应的方程确定另一个变量的值;当函数中的一个变量的取值范围确定时,可由相应的不等式确定另一个变量的取值范围,你能用函数的图像解释一次函数、一元一次方程、一元一次不等式之间的关系吗
复习题
复习巩固
1. 填空:
(1) A、B 两地相距200 km,一列火车以120 km/h 的速度从 A 地出发驶向 B 地,设 x h后这列火车离 B 地的距离为 y (km),则 y 与 x 之间的函数表达式为_____________________________;
y = 200 -120x (0≤x≤ )
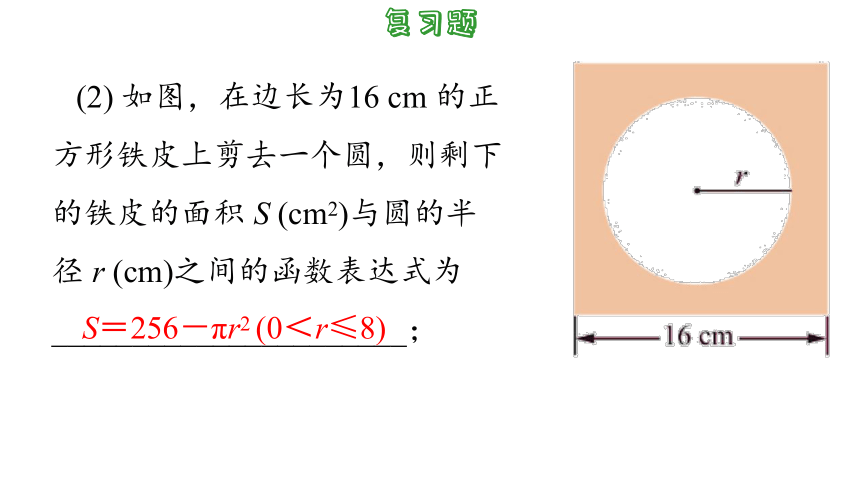
(2) 如图,在边长为16 cm 的正方形铁皮上剪去一个圆,则剩下的铁皮的面积 S (cm2)与圆的半径 r (cm)之间的函数表达式为______________________;
S=256-πr2 (0<r≤8)
(3) 已知一次函数的图像过点 A (2,3),且与 y 轴交点的纵坐标是 4 ,则函数表达式为__________________;
(4) 一根弹簧长 20 cm,最多可挂质量为20 kg的物体,挂上物体后弹簧伸长的长度与所挂物体的质量成正比,如果挂上 5 kg 物体后,弹簧长 22.5 cm,那么弹簧总长度 ,y (cm)与所挂物体质量 x (kg)之间的函数表达式为______________________;
y=-x+4
y=0.5x+20 (0≤x≤20)
2. 已知点P(-2,a)在一次函数 y=3x+1的图像上,求
点 P 的坐标.
∵点P(-2,a)在一次函数y=3+1的图象上.
∴a=3×(-2)+1=-5.
3.已知正比例函数 y=kx 的图像过点 P (3,-3).
(1) 写出这个正比例函数表达式;
由正比例函数 y= kx 的图像过点 P(3, -3)
可得-3=3k,解得 k=-1.
所以正比例函数表达式为 y=-x.
(2) 已知点 A(a,2)在这个正比例函数的图像上,求a的值.
依题意得 2=-a,
所以a=-2.
4. 画出一次函数 y=3x+12 的图像,并利用图像,求:
(1) x=-2、x=-1、x=0.5 时,y的值;
(2) y=3、y=9、y=-3 时,x的值.
解:当x=0时,y=12;
当y=0时,x=-4.
过点(0,12),(-4,0)画直线,即为函数 y=3x+12的图像,如图所示.
(1) x=-2、x=-1、x=0.5 时,y的值;
由图像看出,当x=-2,x=-1,x=0.5时,y的值分别为 6,9,13.5.
(2) y=3、y=9、y=-3 时,x的值.
由图像看出,当 y=3,y=9,y=-3时,x的值分-3, -1, -5.
5. 某水池的容积为 90m3,水池中已有水 10 m3,现按
8m3/h的流量向水池注水.
(1) 写出水池中水的体积 V(m3)与进水时间 t (h)之间的函数表达式,并写出自变量的取值范围.
V=8t+10 (0≤t≤10).
(2)当t=0时,求V的值:当V=90 时,求 t 的值
当t=0时,V=10;
当V=90时,t=10.
(3) 画出这个一次函数的图像.
连接点 (0,10),(10,90) 得线段,即为该函数的图像,如图所示.
6. 用图像法解下列二元一次方程组:
x+y-4=0,
(1)
2x-y+1=0;
4x-y-4=0,
(2)
x+y-6=0;
x+y-4=0,
(1)
2x-y+1=0;
由x+y-4=0,得 y=-x+4;
由 2x-y+1=0,得 y=2x+1.
所以该方程组的解为
x=1,
y=3.
在同一直角坐标系中画出函数
y=-x+4与y=2x+1的图像,
如图所示,其交点为(1,3).
4x-y-4=0,
(2)
x+y-6=0;
由4x-y-4=0,得 y=4x-4;
由x+y-6=0,得 y=-x+6.
在同一直角坐标系中画出函数 y=4x-4与y=x+6的图像,如图所示,其交点为(2,4).
所以该方程组的解为
x=2,
y=4.
灵活运用
7. 已知关于x的一次函数为 y=mx+4m-2.
(1) 若这个函数的图像经过原点,则 m=_________;
(2) 若 m=,则这个函数的图像经过第________象限;
(3) 若 m=,则这个函数的图像经过第_______象限.
一、三、四
一、二、三
8. 已知一次函数 y=2x+b.
(1) 它的图像与两坐标轴所围成的图形的面积等于 4,求b的值;
解:令 x=0,得y=b;令 y= 0,得 x=-.
由题意,得=|b| · | -| =4,
解得 b=±4.
(2) 它的图像经过一次函数 y=-2x+1、y=x+4 图像的交点,求b的值.
解方程组 得
y=-2x+1,
y=x+4,
x=-1,
y=3.
由题意,得 3=2×(-1)+b,解得b=5.
9. 根据某年 7月某市日最高、最低气温折线图,回答下
列问题:
(1)哪几天的气温最高 最高气温是多少
解:(1) 7月26,30,31日的气温最高,最高气温是38C.
(2)哪天的温差最大 最大温差是多少
解:7月 13,19,24日的温差最大,最大温差是10℃.
(3) 哪几天的最高气温持续上升 哪几天的最低气温持续下降
解:7月6日~ 7月8日,7月10日~ 7月14日,7月17日~ 7月19日,7月23日~ 7月26日最高气温持续上升,
7月9日~ 7月11日,7月14日~ 7月17日,7月29日~ 7月31日最低气温持续下降.
10.某海港某日0时到 24 时的水深 y (m)的变化如图所示:
(1) 试根据图中提供的信息填表:
t 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
y 7 9 6.8 5 7 9 7.2 5 7
(2) 一艘货轮计划 16:30 进港卸货,已知该货轮进港时的水深必须在 8m以上,你认为港口能满足该货轮进港的时间要求吗
解:观察图像可知 16:30 的水深约为 8.5m,所以港口能满足该货轮进港的时间要求.
11. 如图,已知 B中的实数与 A 中的实数之间的对应关系是某个一次函数. 若用 y表示 B 中的实数,用工表示 A 中的实数,求y与x之间的函数表达式,并在 B 中写出对应的实数.
解:设y与x 之间的函数表达式为 y=x+b(k≠0),把 x=-3,y=-9;x=0,y=-3 分别代入,得
-9=-3k+6,
-3=b,
解得
k=2,
b=-3.
∴ y与x之间的函数表达式为y=2x-3.
将 x=-,x=-1,x=π 分别代入上式,得
y=-2- 3,y=-5,y= 2π-3.
探索研究
(1) 求这个二元一次方程组的解;
(2)用图像法解这个二元一次方程组;
(3) 从(1)、(2)的解答中你有什么发现
x+y=0,
x+2y-3=0.
12. 已知二元一次方程组
(1) 求这个二元一次方程组的解;
解:由x+y=0,得 x=-2y,
代人 x+2y -3=0,得-2y+2y-3=0,
即-3=0,
显然不成立,所以这个二元一次方程组无解.
(2)用图像法解这个二元一次方程组.
解:由x+y=0,得 y=-x,
过点(0,0),(1, ) 画函数图像,
如图所示.
由 x+2y-3=0,得 y=-x+ .
过点(0, ), (3,0) 画函数图像如图所示.
从图像可以看出,这两条直线平行,所以这个方程组无解.
(3) 从(1)、(2)的解答中你有什么发现
解:若两条直线 y=k1x+b1与 y=k2x+b2平行,则由这两个函数表达式所组成的二元一次方程组无解. 也就是说,当一个二元一次方程组中的两个方程化为y=kx+b的形式后,若k值相等,则这两个函数的图像平行,那么这个二元一次方程组无解.
13. 在七年级下册“二元一次方程组”一章的复习题中,
我们曾研究过如下问题:
探索下列二元一次方程组解的情况:
x-y=1,
2x-y=3.
x-y=1,
2x-2y=2.
x-y=1,
2x-2y=4.
试用二元一次方程组的图像解法,探索上述方程组解的情况,并对解的情况做出解释.
解:(1)由 x-y=1,得 y=-1;
由 2x-y=3,得 y=2x-3.
如图所示,在同一直角坐标系中,
画出一次函数 y=x-1与y=2x-3
的图像,观察图像可知两条直线的交点为 M(2,1),所以方程组 的解是
x-y=1,
2x-y=3
x=2,
y=1.
(2) 由 x-y=1,得 y=x-1;由 2x-2y=2,得 y=x-1,如图所示,在同一直角坐标系中,画出一次函数 y=x-1的图像,此时两直线重合,即两直线有无数个交点,所以方程组 有无数个解.
x-y=1,
2x-2y=2.
(3) 由 x-y=1,得 y=x-1;由 2x×2y=4,得y=x-2. 如图所示,在同一直角坐标系中,画出一次函数 y=x-1与y=x-2的图像,观察图像
得两条直线平行,两函数图
像没有交点,所以方程组
无解.
x-y=1,
2x-2y=4.
本课结束
THANKS!
第6章
一次函数
小结与思考
1. 在一个变化过程中,往往有许多变化的量,其中的一些变量之间常常有着一定的关系,在本章里,我们研究了某些变化过程中两个变量之间的特殊关系——正比例函数关系和一次函数关系.
2. 变量之间的函数关系通常可以用表格、图像和函数表达式表示,这3种表示法各有什么特点
3. 函数 y=kx+6(其中 k、b 为常数,且 k≠0)称为一次函数,一次函数的图像是一条直线. 确定一次函数表达式通常需要几个条件
正比例函数 y=kx(k 是常数,且 k≠0)是特殊的一次函数,它的图像是经过原点且与一次函数 y=kx+b 的图像平行的一条直线,确定一个正比例函数表达式需要几个条件
4. 二元一次方程与一次函数有什么联系 如何利用一次函数的图像求二元次方程组的解
5. 函数刻画现实世界数量的变化及其关系,方程刻画现实世界数量之间的相等关系,不等式刻画现实世界数量之间的不等关系, 当函数中的一个变量的值确定时,可由相应的方程确定另一个变量的值;当函数中的一个变量的取值范围确定时,可由相应的不等式确定另一个变量的取值范围,你能用函数的图像解释一次函数、一元一次方程、一元一次不等式之间的关系吗
复习题
复习巩固
1. 填空:
(1) A、B 两地相距200 km,一列火车以120 km/h 的速度从 A 地出发驶向 B 地,设 x h后这列火车离 B 地的距离为 y (km),则 y 与 x 之间的函数表达式为_____________________________;
y = 200 -120x (0≤x≤ )
(2) 如图,在边长为16 cm 的正方形铁皮上剪去一个圆,则剩下的铁皮的面积 S (cm2)与圆的半径 r (cm)之间的函数表达式为______________________;
S=256-πr2 (0<r≤8)
(3) 已知一次函数的图像过点 A (2,3),且与 y 轴交点的纵坐标是 4 ,则函数表达式为__________________;
(4) 一根弹簧长 20 cm,最多可挂质量为20 kg的物体,挂上物体后弹簧伸长的长度与所挂物体的质量成正比,如果挂上 5 kg 物体后,弹簧长 22.5 cm,那么弹簧总长度 ,y (cm)与所挂物体质量 x (kg)之间的函数表达式为______________________;
y=-x+4
y=0.5x+20 (0≤x≤20)
2. 已知点P(-2,a)在一次函数 y=3x+1的图像上,求
点 P 的坐标.
∵点P(-2,a)在一次函数y=3+1的图象上.
∴a=3×(-2)+1=-5.
3.已知正比例函数 y=kx 的图像过点 P (3,-3).
(1) 写出这个正比例函数表达式;
由正比例函数 y= kx 的图像过点 P(3, -3)
可得-3=3k,解得 k=-1.
所以正比例函数表达式为 y=-x.
(2) 已知点 A(a,2)在这个正比例函数的图像上,求a的值.
依题意得 2=-a,
所以a=-2.
4. 画出一次函数 y=3x+12 的图像,并利用图像,求:
(1) x=-2、x=-1、x=0.5 时,y的值;
(2) y=3、y=9、y=-3 时,x的值.
解:当x=0时,y=12;
当y=0时,x=-4.
过点(0,12),(-4,0)画直线,即为函数 y=3x+12的图像,如图所示.
(1) x=-2、x=-1、x=0.5 时,y的值;
由图像看出,当x=-2,x=-1,x=0.5时,y的值分别为 6,9,13.5.
(2) y=3、y=9、y=-3 时,x的值.
由图像看出,当 y=3,y=9,y=-3时,x的值分-3, -1, -5.
5. 某水池的容积为 90m3,水池中已有水 10 m3,现按
8m3/h的流量向水池注水.
(1) 写出水池中水的体积 V(m3)与进水时间 t (h)之间的函数表达式,并写出自变量的取值范围.
V=8t+10 (0≤t≤10).
(2)当t=0时,求V的值:当V=90 时,求 t 的值
当t=0时,V=10;
当V=90时,t=10.
(3) 画出这个一次函数的图像.
连接点 (0,10),(10,90) 得线段,即为该函数的图像,如图所示.
6. 用图像法解下列二元一次方程组:
x+y-4=0,
(1)
2x-y+1=0;
4x-y-4=0,
(2)
x+y-6=0;
x+y-4=0,
(1)
2x-y+1=0;
由x+y-4=0,得 y=-x+4;
由 2x-y+1=0,得 y=2x+1.
所以该方程组的解为
x=1,
y=3.
在同一直角坐标系中画出函数
y=-x+4与y=2x+1的图像,
如图所示,其交点为(1,3).
4x-y-4=0,
(2)
x+y-6=0;
由4x-y-4=0,得 y=4x-4;
由x+y-6=0,得 y=-x+6.
在同一直角坐标系中画出函数 y=4x-4与y=x+6的图像,如图所示,其交点为(2,4).
所以该方程组的解为
x=2,
y=4.
灵活运用
7. 已知关于x的一次函数为 y=mx+4m-2.
(1) 若这个函数的图像经过原点,则 m=_________;
(2) 若 m=,则这个函数的图像经过第________象限;
(3) 若 m=,则这个函数的图像经过第_______象限.
一、三、四
一、二、三
8. 已知一次函数 y=2x+b.
(1) 它的图像与两坐标轴所围成的图形的面积等于 4,求b的值;
解:令 x=0,得y=b;令 y= 0,得 x=-.
由题意,得=|b| · | -| =4,
解得 b=±4.
(2) 它的图像经过一次函数 y=-2x+1、y=x+4 图像的交点,求b的值.
解方程组 得
y=-2x+1,
y=x+4,
x=-1,
y=3.
由题意,得 3=2×(-1)+b,解得b=5.
9. 根据某年 7月某市日最高、最低气温折线图,回答下
列问题:
(1)哪几天的气温最高 最高气温是多少
解:(1) 7月26,30,31日的气温最高,最高气温是38C.
(2)哪天的温差最大 最大温差是多少
解:7月 13,19,24日的温差最大,最大温差是10℃.
(3) 哪几天的最高气温持续上升 哪几天的最低气温持续下降
解:7月6日~ 7月8日,7月10日~ 7月14日,7月17日~ 7月19日,7月23日~ 7月26日最高气温持续上升,
7月9日~ 7月11日,7月14日~ 7月17日,7月29日~ 7月31日最低气温持续下降.
10.某海港某日0时到 24 时的水深 y (m)的变化如图所示:
(1) 试根据图中提供的信息填表:
t 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
y 7 9 6.8 5 7 9 7.2 5 7
(2) 一艘货轮计划 16:30 进港卸货,已知该货轮进港时的水深必须在 8m以上,你认为港口能满足该货轮进港的时间要求吗
解:观察图像可知 16:30 的水深约为 8.5m,所以港口能满足该货轮进港的时间要求.
11. 如图,已知 B中的实数与 A 中的实数之间的对应关系是某个一次函数. 若用 y表示 B 中的实数,用工表示 A 中的实数,求y与x之间的函数表达式,并在 B 中写出对应的实数.
解:设y与x 之间的函数表达式为 y=x+b(k≠0),把 x=-3,y=-9;x=0,y=-3 分别代入,得
-9=-3k+6,
-3=b,
解得
k=2,
b=-3.
∴ y与x之间的函数表达式为y=2x-3.
将 x=-,x=-1,x=π 分别代入上式,得
y=-2- 3,y=-5,y= 2π-3.
探索研究
(1) 求这个二元一次方程组的解;
(2)用图像法解这个二元一次方程组;
(3) 从(1)、(2)的解答中你有什么发现
x+y=0,
x+2y-3=0.
12. 已知二元一次方程组
(1) 求这个二元一次方程组的解;
解:由x+y=0,得 x=-2y,
代人 x+2y -3=0,得-2y+2y-3=0,
即-3=0,
显然不成立,所以这个二元一次方程组无解.
(2)用图像法解这个二元一次方程组.
解:由x+y=0,得 y=-x,
过点(0,0),(1, ) 画函数图像,
如图所示.
由 x+2y-3=0,得 y=-x+ .
过点(0, ), (3,0) 画函数图像如图所示.
从图像可以看出,这两条直线平行,所以这个方程组无解.
(3) 从(1)、(2)的解答中你有什么发现
解:若两条直线 y=k1x+b1与 y=k2x+b2平行,则由这两个函数表达式所组成的二元一次方程组无解. 也就是说,当一个二元一次方程组中的两个方程化为y=kx+b的形式后,若k值相等,则这两个函数的图像平行,那么这个二元一次方程组无解.
13. 在七年级下册“二元一次方程组”一章的复习题中,
我们曾研究过如下问题:
探索下列二元一次方程组解的情况:
x-y=1,
2x-y=3.
x-y=1,
2x-2y=2.
x-y=1,
2x-2y=4.
试用二元一次方程组的图像解法,探索上述方程组解的情况,并对解的情况做出解释.
解:(1)由 x-y=1,得 y=-1;
由 2x-y=3,得 y=2x-3.
如图所示,在同一直角坐标系中,
画出一次函数 y=x-1与y=2x-3
的图像,观察图像可知两条直线的交点为 M(2,1),所以方程组 的解是
x-y=1,
2x-y=3
x=2,
y=1.
(2) 由 x-y=1,得 y=x-1;由 2x-2y=2,得 y=x-1,如图所示,在同一直角坐标系中,画出一次函数 y=x-1的图像,此时两直线重合,即两直线有无数个交点,所以方程组 有无数个解.
x-y=1,
2x-2y=2.
(3) 由 x-y=1,得 y=x-1;由 2x×2y=4,得y=x-2. 如图所示,在同一直角坐标系中,画出一次函数 y=x-1与y=x-2的图像,观察图像
得两条直线平行,两函数图
像没有交点,所以方程组
无解.
x-y=1,
2x-2y=4.
本课结束
THANKS!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
