2023-2024学年苏科版数学七年级上册4.2 解一元一次方程课件 (1-4课时) 90张PPT
文档属性
| 名称 | 2023-2024学年苏科版数学七年级上册4.2 解一元一次方程课件 (1-4课时) 90张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 19:35:31 | ||
图片预览






文档简介
(共90张PPT)
4.2 解一元一次方程
课时1
方程的解和等式的性质
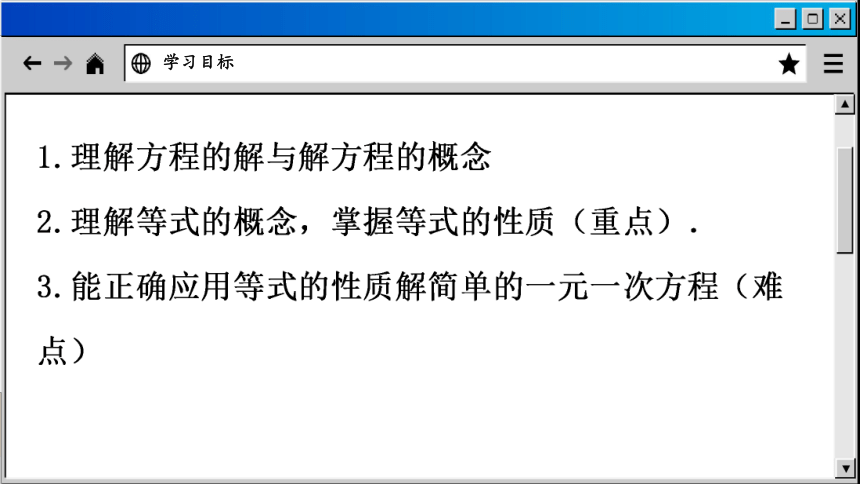
学习目标
如何求出方程中x的值呢?
新课导入
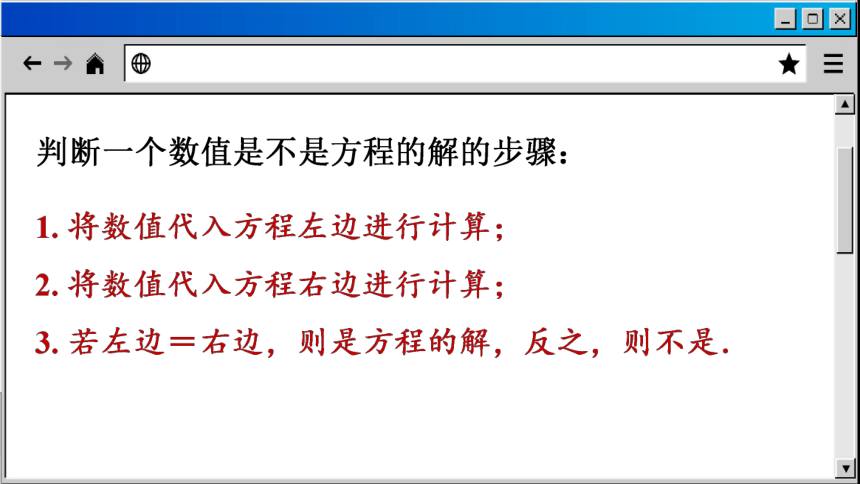
知识点1 解方程和方程的解
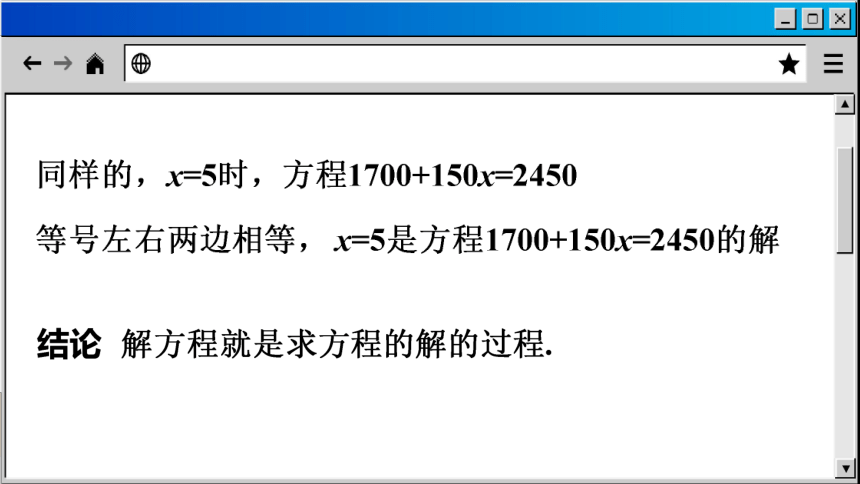
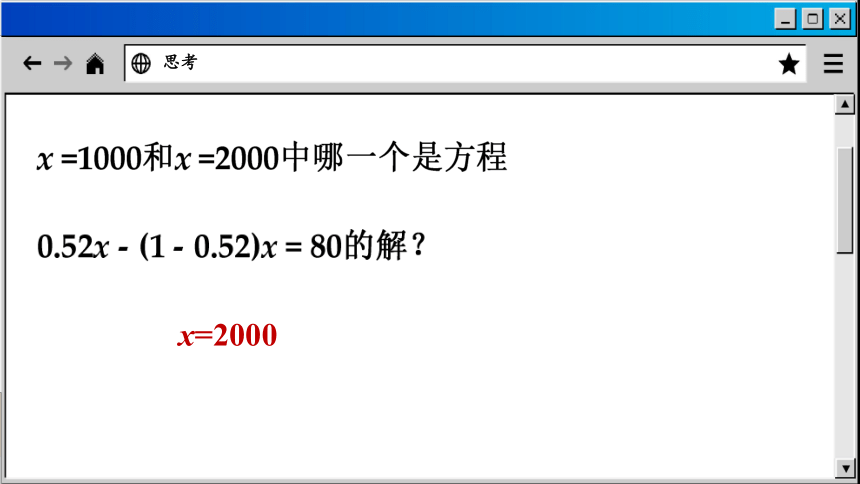
x=2000
思考
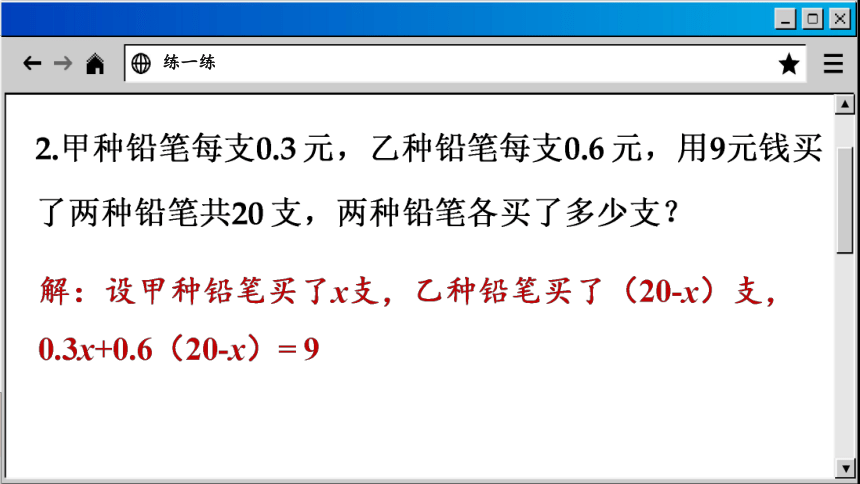
练一练
练一练
练一练
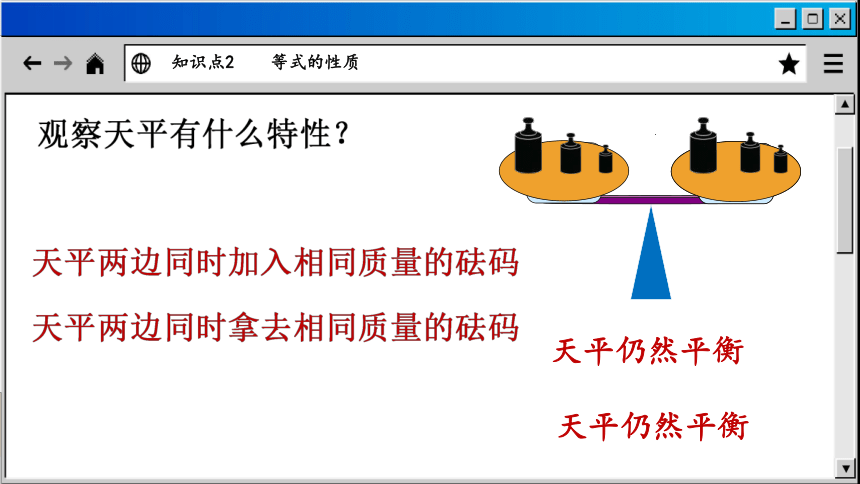
天平仍然平衡
天平仍然平衡
知识点2 等式的性质
+
—
知识点3 利用等式的性质解简单的一元一次方程
解一元一次方程要“化归”x=a的形式
解: (1)两边加5,得 x-5+5=6+5.
于是 x=11.
检验: 当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
练一练
1. x=3,x=0,x=-2,各是下列哪个方程的解?
(1)5x+7=7-2x; (2)6x-8=8x-4; (3)3x-2=4+x.
当堂小练
3. 如果mx=my,那么下列等式中不一定成立的是( )
A.mx+1=my+1
B.mx-3=my-3
C.-mx=-my
D.x=y
D
m≠0
4. 利用等式的性质解下列方程并检验.
(1)5- x=-5
当堂小练
(2)
一个两位数个位上的数是1,十位上的数是x,把1与x对调,新两位数比原两位数小18,试列出关于x的方程,并解这个方程.
D
拓展与延伸
课时2 移向法解方程
解:移项,得
3x + 2x = 32 – 7
合并同类项,得
5x = 25
系数化为1,得
x = 5
解:移项,得
合并同类项,得
系数化为1,得
例题1
例题2
练一练
练一练
1. 对于方程– 3x – 7=12x+6,下列移项正确的是( )
A. – 3x – 12x=6+7 B. – 3x+12x= – 7+6
C. – 3x – 12x=7-6 D.12x – 3x=6+7
2. 对方程 7x = 6 + 4x 进行移项,得___________,合并同类项,得_________,系数化为1,得________.
A
当堂小练
7x – 4x = 6
3x = 6
x = 2
拓展与延伸
课时3 去括号法解方程
移项
合并同类项
系数化为1
移项时要变号
把同类项的系数相加作为所
得项的系数,字母部分不变
方程两边同时除以未知数前
面的系数
移项
合并同类项
月平均用电量×n(月数)=n个月用电量
知识点1 解方程— 去括号
怎样解这个方程?
这个方程与我们前面
研究过的方程有什么
不同?
设上半年平均每月用电x kW·h.
思考
去括号
移项
合并同类项
系数化为1
例题1
练一练
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
练一练
1. 对方程 25b – (b – 5)= 29 去括号,得________________,移项,得_______________,合并同类项,得_________,系数化为1,得___________.
25b – b + 5 = 29
25b – b = 29 – 5
24b = 24
b = 1
当堂小练
2. 买两种布料共138米,花了540元.其中蓝布料每米3元,黑布料每米5元,两种布料各买了多少米?
当堂小练
拓展与延伸
解:由题意得
去括号,得
移项、合并同类项,得 –x = 8
系数化为1,得x = –8
课时4 去分母法解方程
丢番图的墓志铭
你知道丢番图去世时的年龄吗 你认为本题用算术方法解方便,还是用方程方法解方便?
知识点1 解方程—去分母
合并同类项,得
系数化为1,得
这样做的依据是什么
等式的性质2
下面的框图表示解这个方程的流程.
练一练
1. 解方程 时,去分母正确的是( )
A. 3x-1 = 2(x-1)
B. 3x-6 = 2(x-1)
C. 3x-6 = 2x-1
D. 3x-3 = 2x-1
B
当堂小练
2. 解方程:
去分母
去括号
移项
合并同类项
系数化为1
3. 列方程解答下面问题. y的3倍与1.5的和的二分之一等于y与1的差的四分之一,求y.
有一些相同的房间需要粉刷墙面,一天3名一级技工去粉刷8个房间,结果其中有50 m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40 m2墙面,每名一级技工比二级技工一天多粉刷10 m2墙面,求每个房间需要粉刷的墙面面积.
D
拓展与延伸
4.2 解一元一次方程
课时1
方程的解和等式的性质
学习目标
如何求出方程中x的值呢?
新课导入
知识点1 解方程和方程的解
x=2000
思考
练一练
练一练
练一练
天平仍然平衡
天平仍然平衡
知识点2 等式的性质
+
—
知识点3 利用等式的性质解简单的一元一次方程
解一元一次方程要“化归”x=a的形式
解: (1)两边加5,得 x-5+5=6+5.
于是 x=11.
检验: 当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
练一练
1. x=3,x=0,x=-2,各是下列哪个方程的解?
(1)5x+7=7-2x; (2)6x-8=8x-4; (3)3x-2=4+x.
当堂小练
3. 如果mx=my,那么下列等式中不一定成立的是( )
A.mx+1=my+1
B.mx-3=my-3
C.-mx=-my
D.x=y
D
m≠0
4. 利用等式的性质解下列方程并检验.
(1)5- x=-5
当堂小练
(2)
一个两位数个位上的数是1,十位上的数是x,把1与x对调,新两位数比原两位数小18,试列出关于x的方程,并解这个方程.
D
拓展与延伸
课时2 移向法解方程
解:移项,得
3x + 2x = 32 – 7
合并同类项,得
5x = 25
系数化为1,得
x = 5
解:移项,得
合并同类项,得
系数化为1,得
例题1
例题2
练一练
练一练
1. 对于方程– 3x – 7=12x+6,下列移项正确的是( )
A. – 3x – 12x=6+7 B. – 3x+12x= – 7+6
C. – 3x – 12x=7-6 D.12x – 3x=6+7
2. 对方程 7x = 6 + 4x 进行移项,得___________,合并同类项,得_________,系数化为1,得________.
A
当堂小练
7x – 4x = 6
3x = 6
x = 2
拓展与延伸
课时3 去括号法解方程
移项
合并同类项
系数化为1
移项时要变号
把同类项的系数相加作为所
得项的系数,字母部分不变
方程两边同时除以未知数前
面的系数
移项
合并同类项
月平均用电量×n(月数)=n个月用电量
知识点1 解方程— 去括号
怎样解这个方程?
这个方程与我们前面
研究过的方程有什么
不同?
设上半年平均每月用电x kW·h.
思考
去括号
移项
合并同类项
系数化为1
例题1
练一练
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
练一练
1. 对方程 25b – (b – 5)= 29 去括号,得________________,移项,得_______________,合并同类项,得_________,系数化为1,得___________.
25b – b + 5 = 29
25b – b = 29 – 5
24b = 24
b = 1
当堂小练
2. 买两种布料共138米,花了540元.其中蓝布料每米3元,黑布料每米5元,两种布料各买了多少米?
当堂小练
拓展与延伸
解:由题意得
去括号,得
移项、合并同类项,得 –x = 8
系数化为1,得x = –8
课时4 去分母法解方程
丢番图的墓志铭
你知道丢番图去世时的年龄吗 你认为本题用算术方法解方便,还是用方程方法解方便?
知识点1 解方程—去分母
合并同类项,得
系数化为1,得
这样做的依据是什么
等式的性质2
下面的框图表示解这个方程的流程.
练一练
1. 解方程 时,去分母正确的是( )
A. 3x-1 = 2(x-1)
B. 3x-6 = 2(x-1)
C. 3x-6 = 2x-1
D. 3x-3 = 2x-1
B
当堂小练
2. 解方程:
去分母
去括号
移项
合并同类项
系数化为1
3. 列方程解答下面问题. y的3倍与1.5的和的二分之一等于y与1的差的四分之一,求y.
有一些相同的房间需要粉刷墙面,一天3名一级技工去粉刷8个房间,结果其中有50 m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40 m2墙面,每名一级技工比二级技工一天多粉刷10 m2墙面,求每个房间需要粉刷的墙面面积.
D
拓展与延伸
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
