2023-2024学年苏科版数学七年级上册第5章 走进图形世界:5.3 展开与折叠课件 (1-2课时) 32张PPT
文档属性
| 名称 | 2023-2024学年苏科版数学七年级上册第5章 走进图形世界:5.3 展开与折叠课件 (1-2课时) 32张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 20:00:52 | ||
图片预览





文档简介
(共32张PPT)
5.3 展开与折叠
课时1 展开
1.知道一些简单的立体图形的展开图. (重点、难点)
2.在平面图形和立体图形互相转换的过程中,初步建立空间观念. (难点)
学习目标
你会将下列几何体展开成平面图形吗?画出示意图.
新课导入
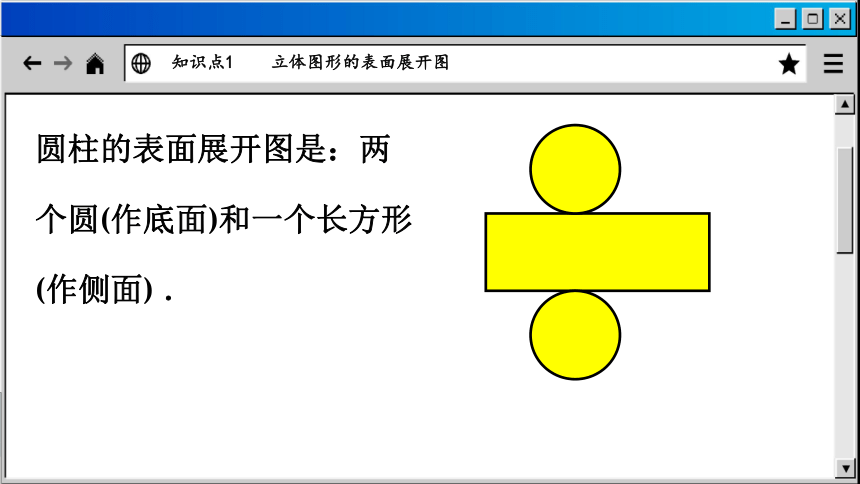
圆柱的表面展开图是:两个圆(作底面)和一个长方形(作侧面) .
知识点1 立体图形的表面展开图
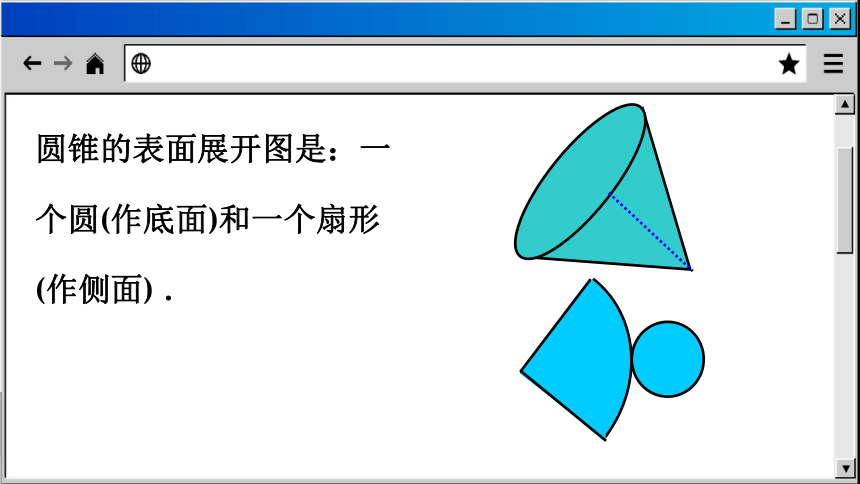
圆锥的表面展开图是:一个圆(作底面)和一个扇形(作侧面) .
1.对于同一个立体图形,当我们按不同的方式展开时,得到的平面展开图是不一样的.
2.不是所有的立体图形都可以展开,如球就不能展开.
如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来.
练一练
如何把一个正方体的表面沿棱剪开,展开成一个平面图形?分组讨论并尝试剪一剪.
注意:剪开正方体棱的过程中,
正方体的6个面中每个面至少有一条棱与其他面相连 .
知识点2 正方体的表面展开图
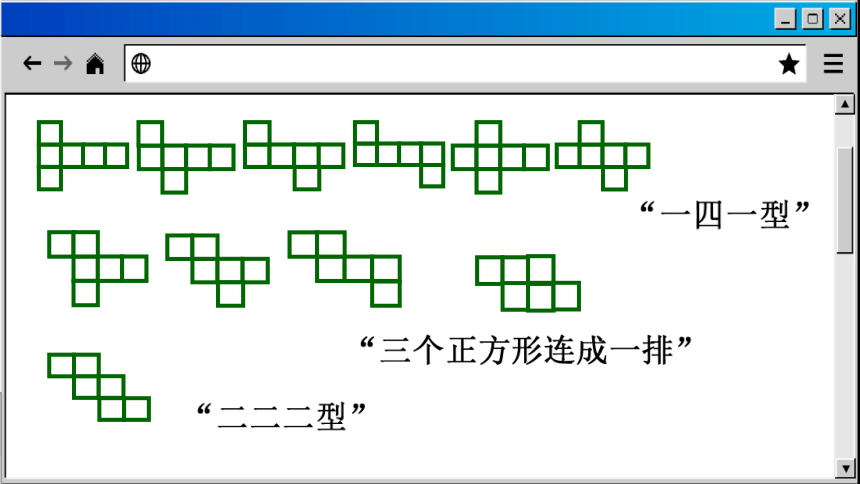
将一个正方体沿棱剪开,并展开成一个平面图形,你能得到哪些图形?
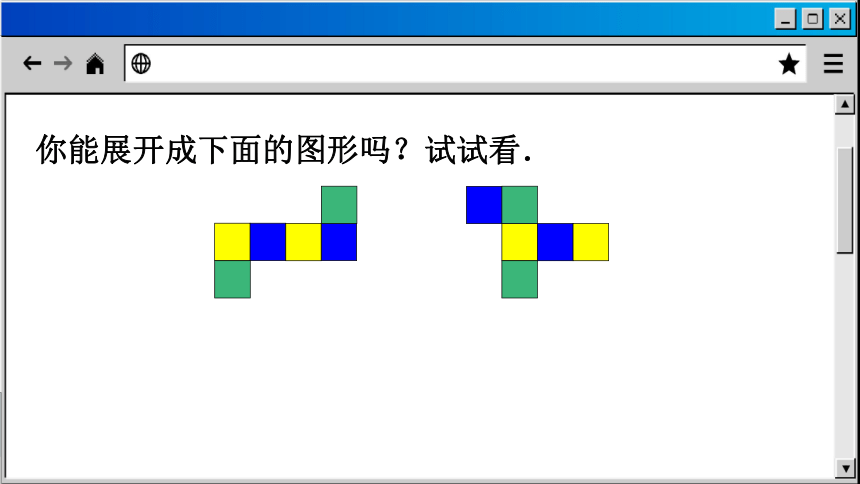
你能展开成下面的图形吗?试试看.
以下图形无法折叠成正方体,请记住!
一字形
田字格
凹字形
凸宝盖
“L”形
一二三
难点突破:
课时2 折叠
在平面图形和立体图形互相转换的过程中,初步建立空间观念. (难点)
学习目标
下面图形经过折叠能否围成棱柱?
(1)
(2)
(3)
新课导入
①侧面数(4个)≠底面边数(3条),不能围成棱柱.
②可以折成棱柱.
③两底面在侧面展开图的同一端,不在两端,所以不能围成棱柱.
如果“你”在前面,那么谁在后面?
你
太
棒
了
!
们
前
右
上
后
左
下
答:棒
知识点1 将表面展开图折叠成立体图形
将展开图折叠成立体图形与立体图形的展开是互逆的过程.
如图所示的立方体,如果把它展开,可以是下列图形中的( )
(B)
(A)
(C)
(D)
D
练一练
如图,将正方体展开图折叠后可粘成A、B、C中哪个正方体? ( )
A
B
C
A
练一练
请你找到对面的朋友:(相同字母代表相对面)
B
A
C
A
C
B
B
A
A
C
B
A
A
B
C
C
C
B
字母分布规律:
1、展开后,在一直线上的三个连续正方形,两端的两个正方形是相对面,字母相同。
2、展开后有公共边或公共顶点的两个正方形不可能是相对面,字母不相同。
1.下图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
A B C D
B
当堂小练
2.下列图形中,是正方体展开图的打“√”.
3.如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它最远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。
.
一只蚂蚁
在点A处
A
B
在点B
发现食
物
.
A
B1
B2
.
.
.
拓展与延伸
4.下面这些图形中,能通过折叠围成正方体的是 _______________.
对其中不能围成正方体的图形,如何移动其中一个小正方形到新的位置使它能折叠成正方体?
(1)
(4)
(3)
(2)
(1)、(2)、(3)
5.如图,这是一个正方体的展开图,如果将它组成原来的正方体,哪些点与点C重合?
A
B
C
D
E
F
G
H
I
J
K
L
M
N
解:M和K.
下面是一长方体的表面展开图,每个面内都标注了字母,请根据
要求回答问题(字母都在多面体的外表面):
(1)如果面 A 在多面体的底部,那么哪一面会在上面?
B
A
C
D
F
E
F
拓展与延伸
(2)如果面 F 在前面,从左面看是面 B ,那么哪一面会在上面?
(3)如果从右面看是面 C,面 D 在后面,那么哪一面会在上面?
A
C
展开
立体图形的表面展开图
正方体的表面展开图
课堂小结
展开图
立体图
展开
折叠
5.3 展开与折叠
课时1 展开
1.知道一些简单的立体图形的展开图. (重点、难点)
2.在平面图形和立体图形互相转换的过程中,初步建立空间观念. (难点)
学习目标
你会将下列几何体展开成平面图形吗?画出示意图.
新课导入
圆柱的表面展开图是:两个圆(作底面)和一个长方形(作侧面) .
知识点1 立体图形的表面展开图
圆锥的表面展开图是:一个圆(作底面)和一个扇形(作侧面) .
1.对于同一个立体图形,当我们按不同的方式展开时,得到的平面展开图是不一样的.
2.不是所有的立体图形都可以展开,如球就不能展开.
如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来.
练一练
如何把一个正方体的表面沿棱剪开,展开成一个平面图形?分组讨论并尝试剪一剪.
注意:剪开正方体棱的过程中,
正方体的6个面中每个面至少有一条棱与其他面相连 .
知识点2 正方体的表面展开图
将一个正方体沿棱剪开,并展开成一个平面图形,你能得到哪些图形?
你能展开成下面的图形吗?试试看.
以下图形无法折叠成正方体,请记住!
一字形
田字格
凹字形
凸宝盖
“L”形
一二三
难点突破:
课时2 折叠
在平面图形和立体图形互相转换的过程中,初步建立空间观念. (难点)
学习目标
下面图形经过折叠能否围成棱柱?
(1)
(2)
(3)
新课导入
①侧面数(4个)≠底面边数(3条),不能围成棱柱.
②可以折成棱柱.
③两底面在侧面展开图的同一端,不在两端,所以不能围成棱柱.
如果“你”在前面,那么谁在后面?
你
太
棒
了
!
们
前
右
上
后
左
下
答:棒
知识点1 将表面展开图折叠成立体图形
将展开图折叠成立体图形与立体图形的展开是互逆的过程.
如图所示的立方体,如果把它展开,可以是下列图形中的( )
(B)
(A)
(C)
(D)
D
练一练
如图,将正方体展开图折叠后可粘成A、B、C中哪个正方体? ( )
A
B
C
A
练一练
请你找到对面的朋友:(相同字母代表相对面)
B
A
C
A
C
B
B
A
A
C
B
A
A
B
C
C
C
B
字母分布规律:
1、展开后,在一直线上的三个连续正方形,两端的两个正方形是相对面,字母相同。
2、展开后有公共边或公共顶点的两个正方形不可能是相对面,字母不相同。
1.下图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
A B C D
B
当堂小练
2.下列图形中,是正方体展开图的打“√”.
3.如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它最远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。
.
一只蚂蚁
在点A处
A
B
在点B
发现食
物
.
A
B1
B2
.
.
.
拓展与延伸
4.下面这些图形中,能通过折叠围成正方体的是 _______________.
对其中不能围成正方体的图形,如何移动其中一个小正方形到新的位置使它能折叠成正方体?
(1)
(4)
(3)
(2)
(1)、(2)、(3)
5.如图,这是一个正方体的展开图,如果将它组成原来的正方体,哪些点与点C重合?
A
B
C
D
E
F
G
H
I
J
K
L
M
N
解:M和K.
下面是一长方体的表面展开图,每个面内都标注了字母,请根据
要求回答问题(字母都在多面体的外表面):
(1)如果面 A 在多面体的底部,那么哪一面会在上面?
B
A
C
D
F
E
F
拓展与延伸
(2)如果面 F 在前面,从左面看是面 B ,那么哪一面会在上面?
(3)如果从右面看是面 C,面 D 在后面,那么哪一面会在上面?
A
C
展开
立体图形的表面展开图
正方体的表面展开图
课堂小结
展开图
立体图
展开
折叠
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
