多边形的内外角[下学期]
文档属性
| 名称 | 多边形的内外角[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-02-27 00:00:00 | ||
图片预览



文档简介
课件14张PPT。答:15边形的内角和是23400例1:求15边形内角和的度数。 多边形的内角和n边形的内角和为(n-2)×1800解:(n-2)×1800=(15-2)×1800= 23400巩固练习一:1、七边形内角和为( )900°2、十边形内角和为( )1440°3、十七边形内角和为( )2700°4、八边形内角和为( )1080°巩固练习二:1、多边形内角和为1260°则它是
( )边形。2、多边形内角和为1080°则它是
( )边形。 3、多边形内角和为1800°则它是
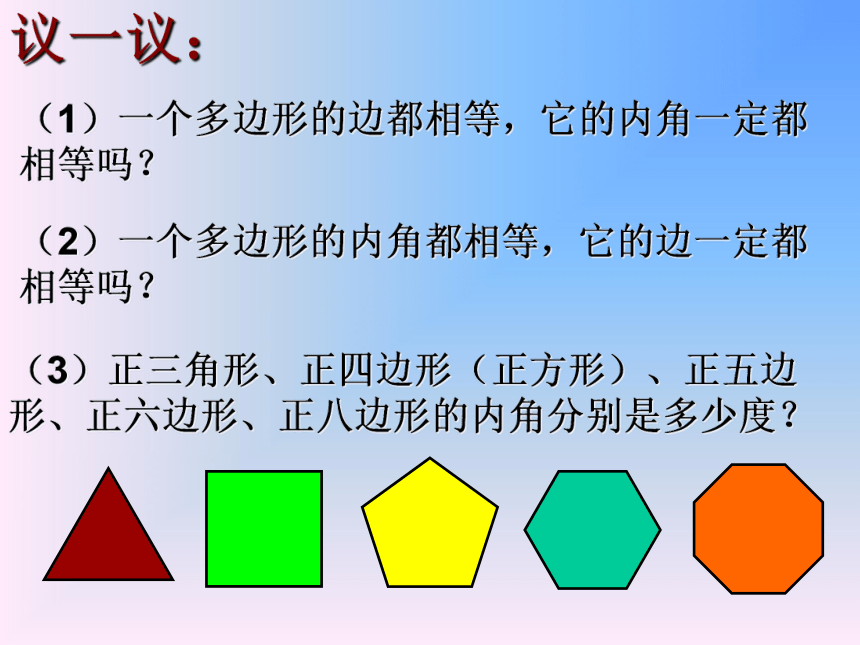
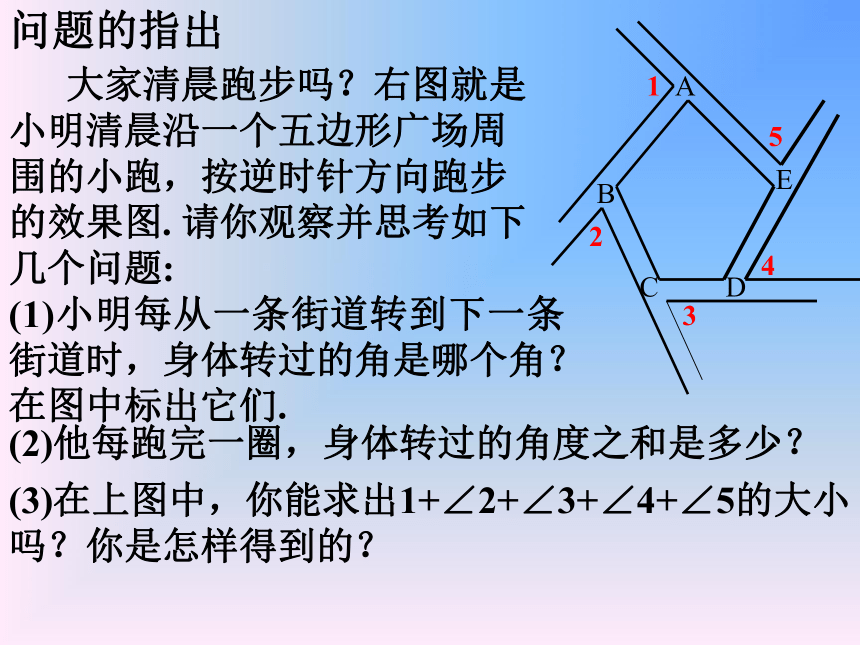
( )边形。九八十二议一议:(1)一个多边形的边都相等,它的内角一定都相等吗?(2)一个多边形的内角都相等,它的边一定都相等吗?(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?问题的指出 大家清晨跑步吗?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?
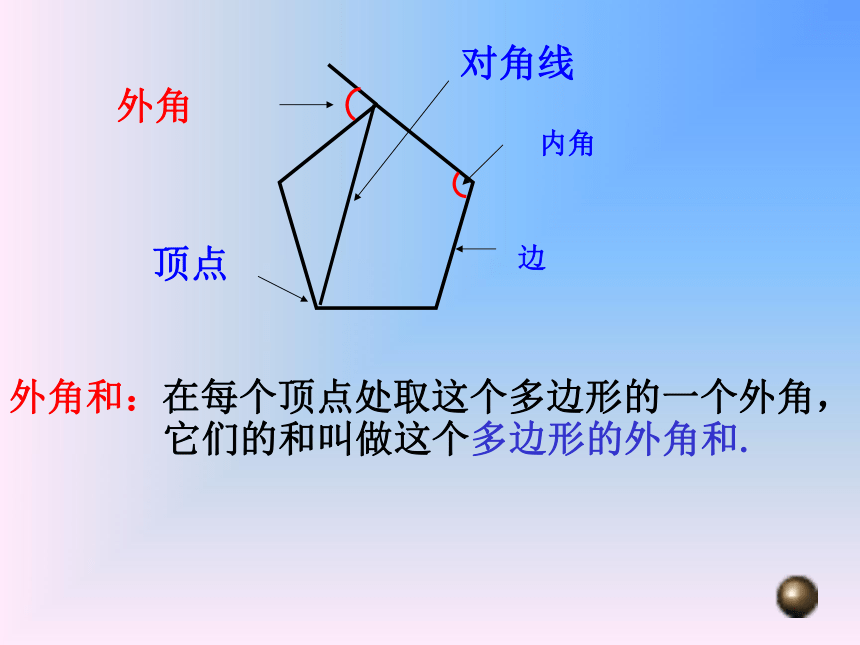
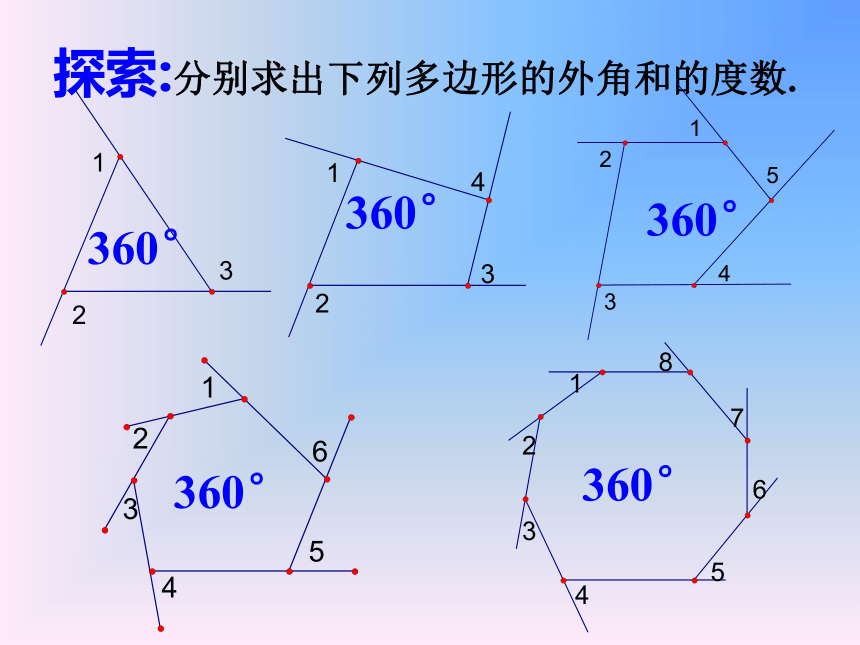
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?顶点内角边外角对角线 探索:分别求出下列多边形的外角和的度数.360° 360° 360° 360° 360° 猜想与说理:n边形的外角和是多少度呢? 答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°. 定理:多边形的外角和都等于360°. 多边形的外角和n边形的外角和为360°例:一个多边形的内角和等
于它的外角和的3倍,它
是几边形?1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°CC巩固练习三: 课堂练习:1.一个多边形的外角都等于60°,这个多边形是n边形? 解:∵多边形的外角和等于360°
∴这个多边形的边数是:360÷60=6
答:这个多边形是六边形. 课堂练习:2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分,这种多边形是几边形?为什么? 解:设:这个正多边形的一个内角为x°
则由题图得:3x=360°. x=120°.
再根据多边形的内角和公式得:
n×120°=(n-2)×180°.
解得n=6 . 答:(略) n-3n-23×18004×1800(n-2)×18001232342×18003600360036003600小 结3、n边形的内角和与外角和是多少?n边形的内角和等于(n - 2)?180°多边形的外角和都等于360° 1、 多边形内角的一边与另一边的反向延长线所
组成的角叫做这个多边形的外角 2、在每个顶点处取这个多边形的一个外角,
它们的和叫做这个多边形的外角和.
( )边形。2、多边形内角和为1080°则它是
( )边形。 3、多边形内角和为1800°则它是
( )边形。九八十二议一议:(1)一个多边形的边都相等,它的内角一定都相等吗?(2)一个多边形的内角都相等,它的边一定都相等吗?(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?问题的指出 大家清晨跑步吗?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?顶点内角边外角对角线 探索:分别求出下列多边形的外角和的度数.360° 360° 360° 360° 360° 猜想与说理:n边形的外角和是多少度呢? 答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°. 定理:多边形的外角和都等于360°. 多边形的外角和n边形的外角和为360°例:一个多边形的内角和等
于它的外角和的3倍,它
是几边形?1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144° B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°CC巩固练习三: 课堂练习:1.一个多边形的外角都等于60°,这个多边形是n边形? 解:∵多边形的外角和等于360°
∴这个多边形的边数是:360÷60=6
答:这个多边形是六边形. 课堂练习:2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分,这种多边形是几边形?为什么? 解:设:这个正多边形的一个内角为x°
则由题图得:3x=360°. x=120°.
再根据多边形的内角和公式得:
n×120°=(n-2)×180°.
解得n=6 . 答:(略) n-3n-23×18004×1800(n-2)×18001232342×18003600360036003600小 结3、n边形的内角和与外角和是多少?n边形的内角和等于(n - 2)?180°多边形的外角和都等于360° 1、 多边形内角的一边与另一边的反向延长线所
组成的角叫做这个多边形的外角 2、在每个顶点处取这个多边形的一个外角,
它们的和叫做这个多边形的外角和.
