数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 672.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 22:39:31 | ||
图片预览





文档简介
(共19张PPT)
2.5.1直线与圆的位置关系
选择性必修第一册 第二章《直线和圆的方程》
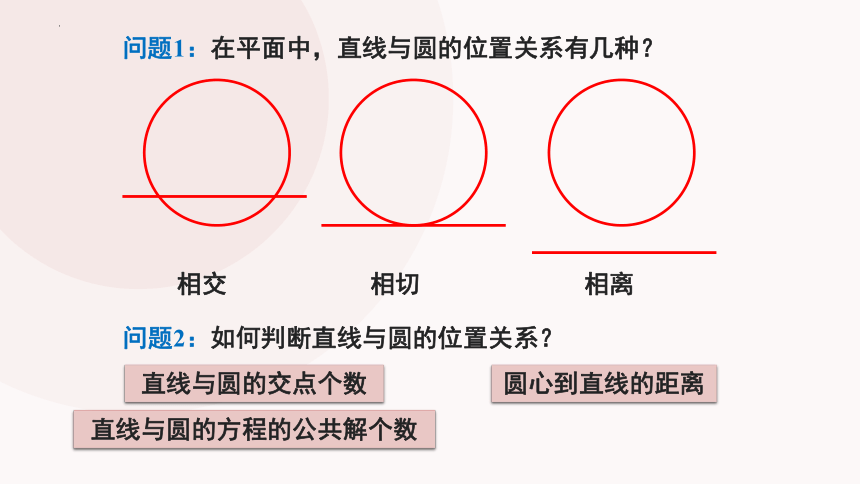
问题1:在平面中,直线与圆的位置关系有几种?
相交
相切
相离
问题2:如何判断直线与圆的位置关系?
直线与圆的交点个数
圆心到直线的距离
直线与圆的方程的公共解个数
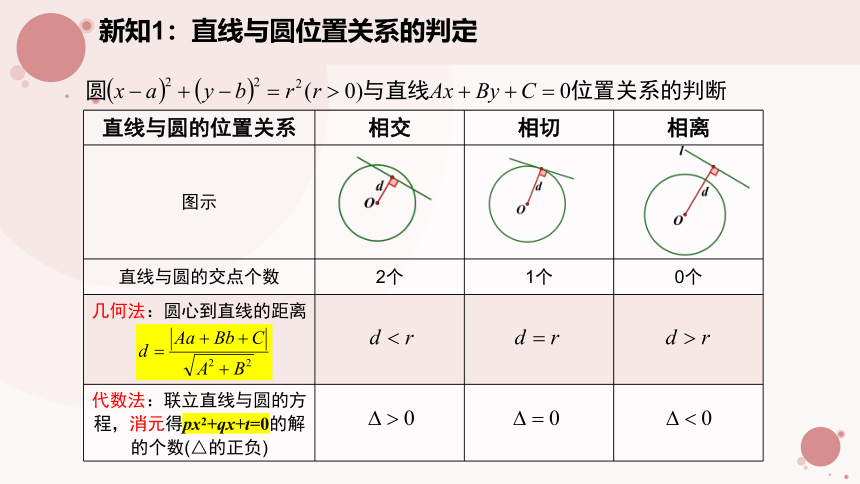
新知1:直线与圆位置关系的判定
直线与圆的位置关系 相交 相切 相离
图示
直线与圆的交点个数 2个 1个 0个
几何法:圆心到直线的距离
代数法:联立直线与圆的方程,消元得px2+qx+t=0的解的个数(△的正负)
基础巩固:直线与圆位置关系的判定(不含参)
问题3: 如何求直线l与圆C的交点坐标?
①
几何法:计算量小;
代数法:可求交点.
基础巩固:直线与圆位置关系的判定(含参)
a<-1或a>3
题型1:过定点的直线与圆的位置关系
相交
升级巩固:过定点的直线与圆位置关系
解:(代数法)联立直线与圆的方程,消去y得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
新知2:直线与圆的相交弦
1.弦:连接圆上任意两点的线段。
①直径是圆的最长弦;②圆心在弦的中垂线上.
2.弦心距:圆心到弦所在直线的距离;
3.垂径定理:垂直于弦的直径平分这条弦,且平分弦所对的两条弧。
4.求弦长:
①两点距离:联立直线与圆的方程求两交点A,B的坐标
②勾股/垂径定理:
③弦长公式:
弦心距
(斜率存在)
(斜率存在
且不为0)
基础巩固:求直线被圆所截得的弦长
①
要点小结
直线与圆的位置关系 相交 相切 相离
图示
直线与圆的交点个数 2个 1个 0个
几何法:圆心到直线的距离
代数法:联立直线与圆的方程,消元得px2+qx+t=0的解的个数(△的正负)
可求交点
计算量小
要点小结
垂径定理:垂直于弦的直径平分这条弦,且平分弦所对的两条弧。
②勾股+垂径定理:
③万能弦长公式:
(斜率存在)
(斜率存在不为0)
求弦长的方法:
①两点距离:联立直线与圆的方程求两交点A,B的坐标
联立线/圆方程,消元得px2+qx+t =0&韦达定理x1+x2,x1x2
题型2:知弦长,求弦所在直线方程
目标:求斜率
新知3:直线与圆的切线
1.直线与圆的切线的性质
①圆心到切线的距离等于半径;
②圆心与切点的连线垂直于切线;
③过圆外一点且与圆相切的直线有2条,切线长相等.
2.求圆的切线方程
由垂直求斜率
由d=r求未知量
题型3:求圆的切线方程
圆的切线的性质:
①圆心到切线的距离等于半径(d=r);
②圆心与切点的连线垂直于切线(斜率积为-1);
由d=r求斜率k
题型3:求圆的切线方程
圆的切线的性质:
①圆心到切线的距离等于半径(d=r);
②圆心与切点的连线垂直于切线(斜率积为-1);
综合应用巩固P98
确定目标、数形结合、列式求解
2.求下列条件确定的圆的方程,并画出它们的图形:
(1)圆心为M(3,-5),且与直线x-7y+2=0相切;
(2)圆心在直线y=x上,半径为2,且与直线y=6相切;
(3)半径为,且与直线2x-3y+6=0相切于点(3,4).
目标:求半径
目标:求圆心
目标:求圆心
综合应用巩固P98
确定目标、数形结合、列式求解
3.求直线l:3x-y-6=0被圆C:x +y -2x-4y=0截得的弦AB的长.
4.求圆心在直线3x-y=0上,与x轴相切,且被直线x-y=0截得的弦长为的圆的方程.
5.求与圆C:x +y -x+2y=0关于直线l:x-y+1=0对称的圆的方程.
目标:求圆心/半径
直线与圆综合题的“条件反射”
1.切入点:画图辅助理解
2.看目标:
(1)求直线方程:设直线(考虑斜率是否存在)
(2)求圆的方程:找圆心、半径
3.看题干
(1)见“相切”:由垂直斜率乘积为-1列式(切点已知)
或由圆心到切线距离d=r列式(切点未知)
(2)见“圆的弦长”:构造Rt△,由半弦长、半径、弦心距的关系列式
THANKS
2.5.1直线与圆的位置关系
选择性必修第一册 第二章《直线和圆的方程》
问题1:在平面中,直线与圆的位置关系有几种?
相交
相切
相离
问题2:如何判断直线与圆的位置关系?
直线与圆的交点个数
圆心到直线的距离
直线与圆的方程的公共解个数
新知1:直线与圆位置关系的判定
直线与圆的位置关系 相交 相切 相离
图示
直线与圆的交点个数 2个 1个 0个
几何法:圆心到直线的距离
代数法:联立直线与圆的方程,消元得px2+qx+t=0的解的个数(△的正负)
基础巩固:直线与圆位置关系的判定(不含参)
问题3: 如何求直线l与圆C的交点坐标?
①
几何法:计算量小;
代数法:可求交点.
基础巩固:直线与圆位置关系的判定(含参)
a<-1或a>3
题型1:过定点的直线与圆的位置关系
相交
升级巩固:过定点的直线与圆位置关系
解:(代数法)联立直线与圆的方程,消去y得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
新知2:直线与圆的相交弦
1.弦:连接圆上任意两点的线段。
①直径是圆的最长弦;②圆心在弦的中垂线上.
2.弦心距:圆心到弦所在直线的距离;
3.垂径定理:垂直于弦的直径平分这条弦,且平分弦所对的两条弧。
4.求弦长:
①两点距离:联立直线与圆的方程求两交点A,B的坐标
②勾股/垂径定理:
③弦长公式:
弦心距
(斜率存在)
(斜率存在
且不为0)
基础巩固:求直线被圆所截得的弦长
①
要点小结
直线与圆的位置关系 相交 相切 相离
图示
直线与圆的交点个数 2个 1个 0个
几何法:圆心到直线的距离
代数法:联立直线与圆的方程,消元得px2+qx+t=0的解的个数(△的正负)
可求交点
计算量小
要点小结
垂径定理:垂直于弦的直径平分这条弦,且平分弦所对的两条弧。
②勾股+垂径定理:
③万能弦长公式:
(斜率存在)
(斜率存在不为0)
求弦长的方法:
①两点距离:联立直线与圆的方程求两交点A,B的坐标
联立线/圆方程,消元得px2+qx+t =0&韦达定理x1+x2,x1x2
题型2:知弦长,求弦所在直线方程
目标:求斜率
新知3:直线与圆的切线
1.直线与圆的切线的性质
①圆心到切线的距离等于半径;
②圆心与切点的连线垂直于切线;
③过圆外一点且与圆相切的直线有2条,切线长相等.
2.求圆的切线方程
由垂直求斜率
由d=r求未知量
题型3:求圆的切线方程
圆的切线的性质:
①圆心到切线的距离等于半径(d=r);
②圆心与切点的连线垂直于切线(斜率积为-1);
由d=r求斜率k
题型3:求圆的切线方程
圆的切线的性质:
①圆心到切线的距离等于半径(d=r);
②圆心与切点的连线垂直于切线(斜率积为-1);
综合应用巩固P98
确定目标、数形结合、列式求解
2.求下列条件确定的圆的方程,并画出它们的图形:
(1)圆心为M(3,-5),且与直线x-7y+2=0相切;
(2)圆心在直线y=x上,半径为2,且与直线y=6相切;
(3)半径为,且与直线2x-3y+6=0相切于点(3,4).
目标:求半径
目标:求圆心
目标:求圆心
综合应用巩固P98
确定目标、数形结合、列式求解
3.求直线l:3x-y-6=0被圆C:x +y -2x-4y=0截得的弦AB的长.
4.求圆心在直线3x-y=0上,与x轴相切,且被直线x-y=0截得的弦长为的圆的方程.
5.求与圆C:x +y -x+2y=0关于直线l:x-y+1=0对称的圆的方程.
目标:求圆心/半径
直线与圆综合题的“条件反射”
1.切入点:画图辅助理解
2.看目标:
(1)求直线方程:设直线(考虑斜率是否存在)
(2)求圆的方程:找圆心、半径
3.看题干
(1)见“相切”:由垂直斜率乘积为-1列式(切点已知)
或由圆心到切线距离d=r列式(切点未知)
(2)见“圆的弦长”:构造Rt△,由半弦长、半径、弦心距的关系列式
THANKS
