3.1.1 方程的根与函数的零点(全课时,讲练结合,共40页PPT)
文档属性
| 名称 | 3.1.1 方程的根与函数的零点(全课时,讲练结合,共40页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-15 00:00:00 | ||
图片预览









文档简介
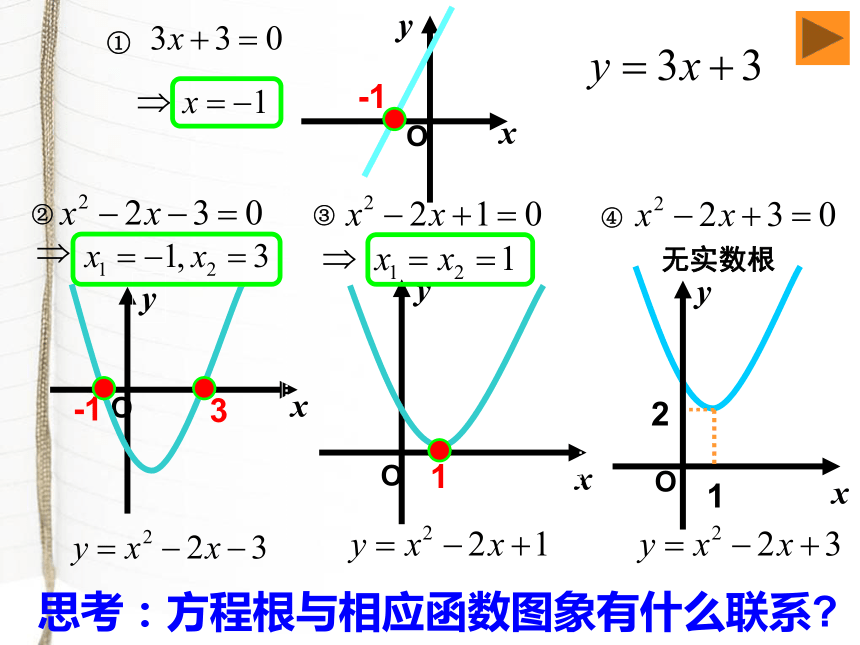
课件40张PPT。中外历史上的方程求解约公元50~100年编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求根方法. 中外历史上的方程求解11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法. 中外历史上的方程求解13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法。 中外历史上的方程求解 国外数学家对方程求解亦有很多研究。9世纪以后,先后发现了一次、二次、三次、四次方程的求根方法;数学史上,人们曾经希望得到一般的五次以上代数方程的根式解,但最后被19世纪挪威数学家阿贝尔证明了五次及五次以上一般方程没有根式解。同样,指数方程、对数方程等超越方程也是没有求根公式的。方程解法史话:数学家方台纳的故事1535年,在意大利有一条轰动一时的新闻:数学家奥罗挑战数学家方台纳,奥罗给方台纳出了30道题,求解x3+5x=10,x3+7x=14,x3+11x=20,……;诸如方程x3+Mx=N,M,N是正整数,比赛时间为20天,方台纳埋头苦干,终于在最后一天解决了这个问题。方程的求解经历了相当漫长的岁月,让我们来感受数学探索的魅力吧!方台纳3.1.1 方程的根与函数的零点探究:求下列方程的实数根,画出相应函数的简图,
并求出函数图象与x轴交点的坐标。问题探究思考:方程根与相应函数图象有什么联系?-13①1②③12无实数根④-1 思考:
一元二次方程ax2+bx+c=0(a≠0)的根
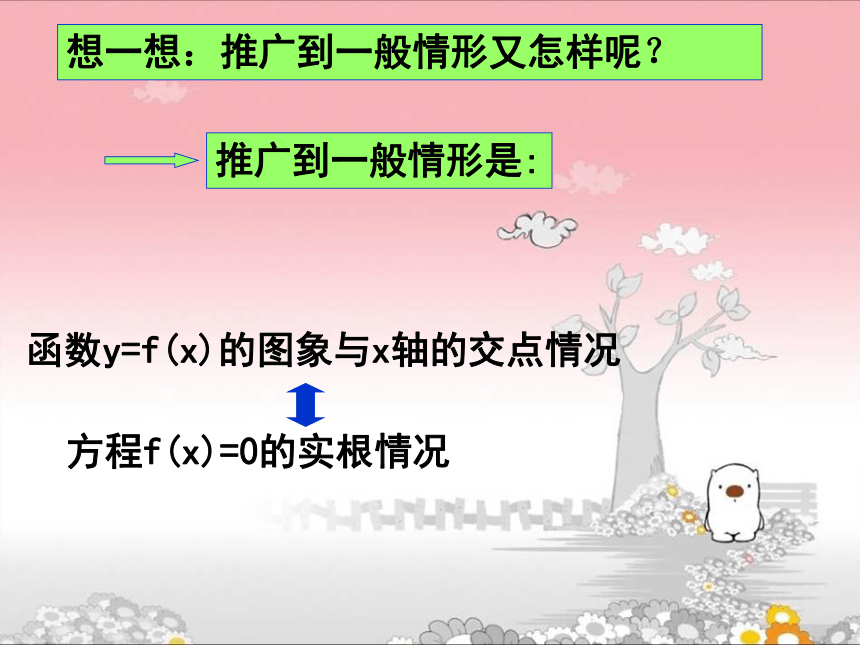
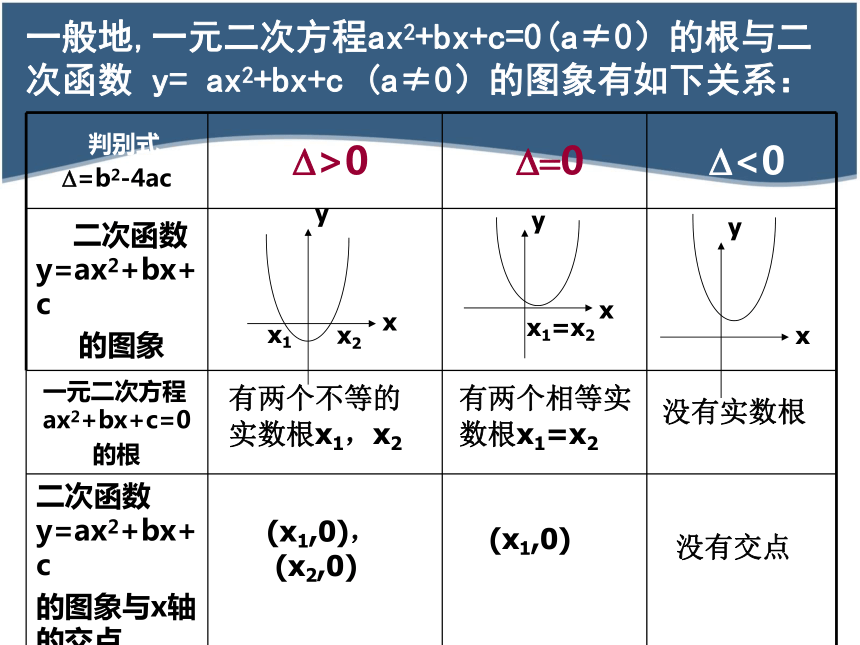
与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?提出问题:一元二次方程 的根与二次函数 的图象有什么关系?结 论: 1.方程根的个数就是函数图象与x轴交点的个数.2.方程的实数根就是函数图象与x轴交点的横坐标.推广到一般情形是:函数y=f(x)的图象与x轴的交点情况方程f(x)=0的实根情况想一想:推广到一般情形又怎样呢?有两个不等的
实数根x1,x2
有两个相等实数根x1=x2没有实数根一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图象有如下关系:(x1,0),
(x2,0) (x1,0)没有交点 对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点。函数零点的定义:注意:零点指的是一个实数;D问题:函数 的零点是( )
A.(-1,0),(3,0)
B. x=-1
C. x=3
D. -1和3 定义:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点(zero point).方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点剖析概念,你能得出什么结论吗?结论:函数y=f(x)的零点就是方程f(x)=0的实数根。代数法图象法问题:你能从下图中分析此函数有几个零点吗?-2-123想一想,怎样求函数的零点呢?求函数的零点有两种方法:
①代数法:求方程f(x)=0的实数根;
②几何法:将它与函数y=f(x)的图象联系起来,并利用函数的性质找出零点。下面我们来探究二次函数的零点个数情况1.用代数法探究结论:二次函数(1)△>0,二次函数有两个零点;(2)△=0,二次函数有一个二重零点或二阶零点;(3)△<0,二次函数没有零点。练习:求下列函数的零点(1)解:令f(x)=-x2+3x+5,
作出函数f(x)的图象,如下: 它与x轴有两个交点,所以方程-x2+3x+5=0有两个不相等的实数根。(1) -x2+3x+5=0课堂练习:P88 1 (2)解:2x(x-2)=-3可化为
2x2-4x+3=0,令f(x)= 2x2-4x
+3 , 作出函数f(x)的图象,如下: 它与x轴没有交点,所以方程2x(x-2)=-3无实数根。(2) 2x(x-2)=-3(3)解:x2 =4x-4可化为x2-4x
+4=0,令f(x)= x2-4x+4,作出函数f(x)的图象,如下: 它与x轴只有一个交点,所以方程x2 =4x-4有两个相等的实数根。(3) x2 =4x-4(4)解:5x2 +2x=3x2 +5可化为
2x2 +2x-5=0,令f(x)=2x2+
2x-5 , 作出函数f(x)的图象,
如下: 它与x轴有两个交点,所以
方程5x2 +2x=3x2 +5有两个不
相等的实数根。(4) 5 x2 +2x=3 x2 +5全优74页典例剖析3.若函数f(x)=x2-ax-b的两个零点是2和3,求函数g(x)=bx2-ax-1的零点.
解:由题意知,函数f(x)=x2-ax-b的两个零点是2和3,
知方程x2-ax-b=0的两个实根是2和3.
故有a=2+3=5,-b=2×3,即b=-6,
因此g(x)=-6x2-5x-1.全优74页变式训练全优99页2、用数形结合法探究(以 为例)观察二次函数 的图象,填空:①在区间[-2,1]上有零点 ;
f(-2)= ;f(1)= ;
f(-2)·f(1) 0。②在区间[2,4]上有零点 ;
f(2)·f(4) 0。-15- 4<3<想一想:怎样判断一个函数在给定区间上是否存在零点呢?让我们来看一个例子第1组第2组探究:现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河? ??问题探究[来源:学科网ZXXK]2018/12/23282018/12/2329问题:如果将定义域改为区间[a,b]观察图像说一说零点个数的情况,有什么发现? 如果函数y=f(x)在区间[a,b]上的图象是连续不断一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点.即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的根.结论连续函数在某个区间上存在零点的判别方法:练习:课本92页 26.根据表格中的数据,可以判断方程ex-x-2=0的一个根所在的最小为区间__________.解析:设f(x)=ex-x-2,∵f(1)=2.78-3=-0.22<0,f(2)=7.39-4=3.39>0.∴f(1)f(2)<0,由根的存在性定理知,方程ex-x-2=0必有一个根在区间(1,2).全优75页能力提高2018/12/2333思考1:若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内会是只有一个零点么?
有零点,至少有一个,但不确定个数,即存在零点。结论ab
x 思考2:若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)>0,则f(x)在区间(a,b)内就一定没有零点么?
思考3:在什么条件下,函数y=f(x)在区间(a,b)上可存在唯一零点?
全优75页基础夯实解:用计算器或计算机作出x、f(x)的对应值表3-1和
图象3.1-3例1:求函数f(x)=lnx+2x-6的零点个数.f(2)<0,f(3)>0即f(2)·f(3)<0函数在区间(2,3)内有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以它仅有一个零点。例1:求函数f(x)=lnx+2x-6的零点个数.将函数f(x)=lnx+2x-6的零点个数转化为函数
g(x)=lnx与h(x)=-2x+6的图象交点的个数。A.0B.1C.2D.3全优99页全优75页能力提高
并求出函数图象与x轴交点的坐标。问题探究思考:方程根与相应函数图象有什么联系?-13①1②③12无实数根④-1 思考:
一元二次方程ax2+bx+c=0(a≠0)的根
与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?提出问题:一元二次方程 的根与二次函数 的图象有什么关系?结 论: 1.方程根的个数就是函数图象与x轴交点的个数.2.方程的实数根就是函数图象与x轴交点的横坐标.推广到一般情形是:函数y=f(x)的图象与x轴的交点情况方程f(x)=0的实根情况想一想:推广到一般情形又怎样呢?有两个不等的
实数根x1,x2
有两个相等实数根x1=x2没有实数根一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图象有如下关系:(x1,0),
(x2,0) (x1,0)没有交点 对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点。函数零点的定义:注意:零点指的是一个实数;D问题:函数 的零点是( )
A.(-1,0),(3,0)
B. x=-1
C. x=3
D. -1和3 定义:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点(zero point).方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点剖析概念,你能得出什么结论吗?结论:函数y=f(x)的零点就是方程f(x)=0的实数根。代数法图象法问题:你能从下图中分析此函数有几个零点吗?-2-123想一想,怎样求函数的零点呢?求函数的零点有两种方法:
①代数法:求方程f(x)=0的实数根;
②几何法:将它与函数y=f(x)的图象联系起来,并利用函数的性质找出零点。下面我们来探究二次函数的零点个数情况1.用代数法探究结论:二次函数(1)△>0,二次函数有两个零点;(2)△=0,二次函数有一个二重零点或二阶零点;(3)△<0,二次函数没有零点。练习:求下列函数的零点(1)解:令f(x)=-x2+3x+5,
作出函数f(x)的图象,如下: 它与x轴有两个交点,所以方程-x2+3x+5=0有两个不相等的实数根。(1) -x2+3x+5=0课堂练习:P88 1 (2)解:2x(x-2)=-3可化为
2x2-4x+3=0,令f(x)= 2x2-4x
+3 , 作出函数f(x)的图象,如下: 它与x轴没有交点,所以方程2x(x-2)=-3无实数根。(2) 2x(x-2)=-3(3)解:x2 =4x-4可化为x2-4x
+4=0,令f(x)= x2-4x+4,作出函数f(x)的图象,如下: 它与x轴只有一个交点,所以方程x2 =4x-4有两个相等的实数根。(3) x2 =4x-4(4)解:5x2 +2x=3x2 +5可化为
2x2 +2x-5=0,令f(x)=2x2+
2x-5 , 作出函数f(x)的图象,
如下: 它与x轴有两个交点,所以
方程5x2 +2x=3x2 +5有两个不
相等的实数根。(4) 5 x2 +2x=3 x2 +5全优74页典例剖析3.若函数f(x)=x2-ax-b的两个零点是2和3,求函数g(x)=bx2-ax-1的零点.
解:由题意知,函数f(x)=x2-ax-b的两个零点是2和3,
知方程x2-ax-b=0的两个实根是2和3.
故有a=2+3=5,-b=2×3,即b=-6,
因此g(x)=-6x2-5x-1.全优74页变式训练全优99页2、用数形结合法探究(以 为例)观察二次函数 的图象,填空:①在区间[-2,1]上有零点 ;
f(-2)= ;f(1)= ;
f(-2)·f(1) 0。②在区间[2,4]上有零点 ;
f(2)·f(4) 0。-15- 4<3<想一想:怎样判断一个函数在给定区间上是否存在零点呢?让我们来看一个例子第1组第2组探究:现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河? ??问题探究[来源:学科网ZXXK]2018/12/23282018/12/2329问题:如果将定义域改为区间[a,b]观察图像说一说零点个数的情况,有什么发现? 如果函数y=f(x)在区间[a,b]上的图象是连续不断一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点.即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的根.结论连续函数在某个区间上存在零点的判别方法:练习:课本92页 26.根据表格中的数据,可以判断方程ex-x-2=0的一个根所在的最小为区间__________.解析:设f(x)=ex-x-2,∵f(1)=2.78-3=-0.22<0,f(2)=7.39-4=3.39>0.∴f(1)f(2)<0,由根的存在性定理知,方程ex-x-2=0必有一个根在区间(1,2).全优75页能力提高2018/12/2333思考1:若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内会是只有一个零点么?
有零点,至少有一个,但不确定个数,即存在零点。结论ab
x 思考2:若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)>0,则f(x)在区间(a,b)内就一定没有零点么?
思考3:在什么条件下,函数y=f(x)在区间(a,b)上可存在唯一零点?
全优75页基础夯实解:用计算器或计算机作出x、f(x)的对应值表3-1和
图象3.1-3例1:求函数f(x)=lnx+2x-6的零点个数.f(2)<0,f(3)>0即f(2)·f(3)<0函数在区间(2,3)内有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以它仅有一个零点。例1:求函数f(x)=lnx+2x-6的零点个数.将函数f(x)=lnx+2x-6的零点个数转化为函数
g(x)=lnx与h(x)=-2x+6的图象交点的个数。A.0B.1C.2D.3全优99页全优75页能力提高
