陕西省榆林市府谷县第三中学2020-2021学年高二上学期期中考试数学(文科)试卷(PDF含答案)
文档属性
| 名称 | 陕西省榆林市府谷县第三中学2020-2021学年高二上学期期中考试数学(文科)试卷(PDF含答案) |  | |
| 格式 | |||
| 文件大小 | 324.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-28 22:53:08 | ||
图片预览

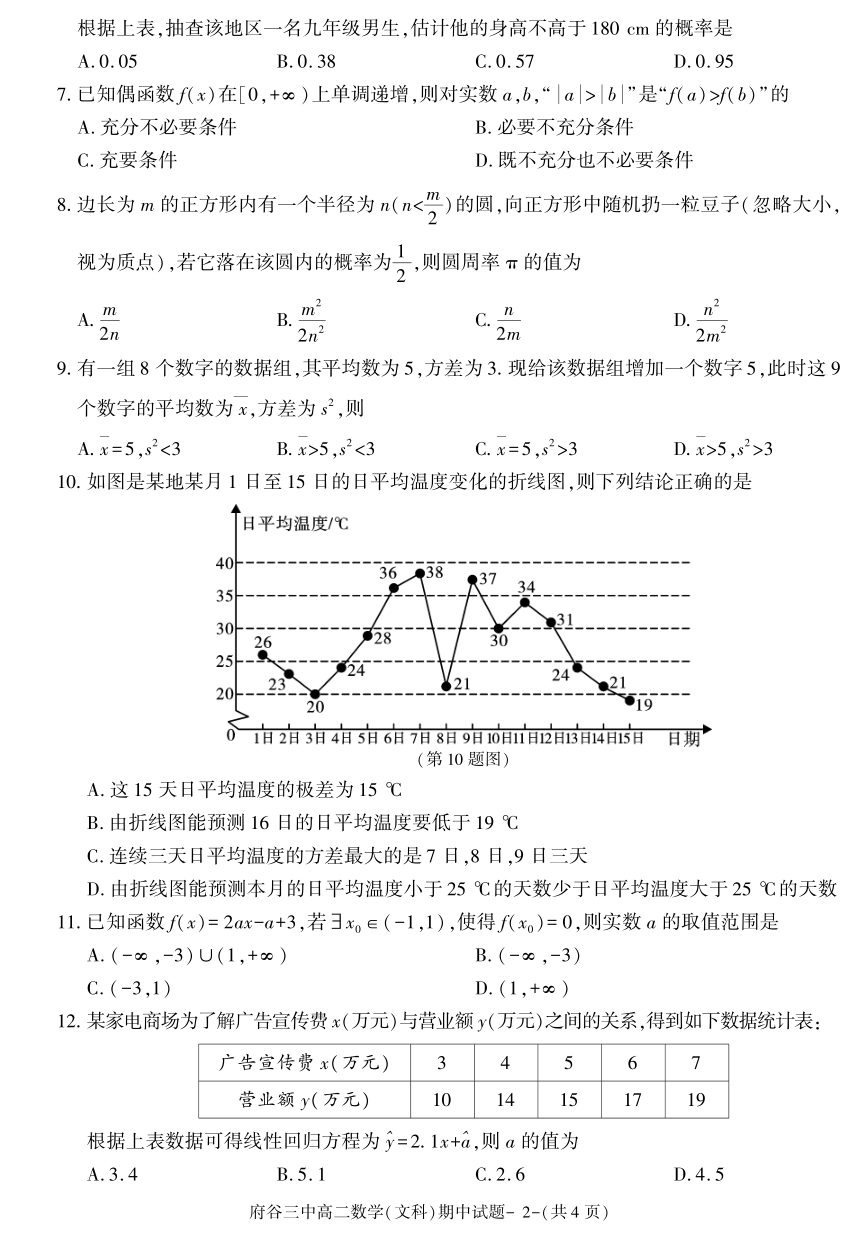

文档简介
府谷三中 2020 ~ 2021 学年度第一学期期中质量检测
高二数学(文科)试题
注意事项:
1. 本试题共 4 页,满分 150 分,时间 120 分钟;
2. 答卷前,考生需准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准考证号;
3. 第Ⅰ卷选择题必须使用 2B 铅笔填涂,第Ⅱ卷非选择题必须使用 0. 5 毫米黑色墨水签字笔书
写,涂写要工整、清晰;
4. 考试结束后,监考员将答题卡按顺序收回,装袋整理;试题卷不回收。
第Ⅰ卷(选择题 共 60 分)
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合
题目要求的)
1. 为了解一批灯泡的使用寿命,从中抽取 20 只灯泡进行测试,在这个问题中,被抽取的 20 只
灯泡的使用寿命是
A. 总体 B. 个体 C. 样本 D. 样本容量
2. 在下列各图中,变量 x,y 具有线性相关关系的是
3. 命题“ x>0,ln x>0”的否定为
A. x>0,ln x≤0 B. x≤0,ln x≤0 C. x>0,ln x<0 D. x>0,ln x≤0
4. 某会场有 28 排,每排有 32 个座位,在一次报告中恰好坐满了听众,报告结束后,为了了解听
众意见,需要抽取 28 名听众进行座谈,则最合理的抽样方法是
A. 抽签法 B. 系统抽样法 C. 分层抽样法 D. 随机数表法
5. 下列命题中是假命题的是
A. x0∈R,lg x0 =0 B. x0∈R,tan x0 =0
C. x∈R,3x>0 D. x∈R,x2>0
6. 为了解某地区九年级男生的身高情况,随机选取了该地区 100 名九年级男生进行测量,他们
的身高 x(cm)统计如下表:
组别(cm) x≤160 160180
人数 15 42 38 5
府谷三中高二数学(文科)期中试题- 1-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
根据上表,抽查该地区一名九年级男生,估计他的身高不高于 180 cm 的概率是
A. 0. 05 B. 0. 38 C. 0. 57 D. 0. 95
7. 已知偶函数 f(x)在[0,+∞ )上单调递增,则对实数 a,b,“ a > b ”是“ f(a)>f(b)”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
8. 边长为 m 的正方形内有一个半径为 n(n2
视为质点),若它落在该圆内的概率为 1 ,则圆周率 π 的值为
2
A. m B. m
2
C. n D. n
2
2n 2n2 2m 2m2
9. 有一组 8 个数字的数据组,其平均数为 5,方差为 3. 现给该数据组增加一个数字 5,此时这 9
个数字的平均数为 x,方差为 s2,则
A. x=5,s2<3 B. x>5,s2<3 C. x=5,s2>3 D. x>5,s2>3
10. 如图是某地某月 1 日至 15 日的日平均温度变化的折线图,则下列结论正确的是
(第 10 题图)
A. 这 15 天日平均温度的极差为 15 ℃
B. 由折线图能预测 16 日的日平均温度要低于 19 ℃
C. 连续三天日平均温度的方差最大的是 7 日,8 日,9 日三天
D. 由折线图能预测本月的日平均温度小于 25 ℃的天数少于日平均温度大于 25 ℃的天数
11. 已知函数 f(x)= 2ax-a+3,若 x0∈(-1,1),使得 f(x0)= 0,则实数 a 的取值范围是
A. (-∞ ,-3)∪(1,+∞ ) B. (-∞ ,-3)
C. (-3,1) D. (1,+∞ )
12. 某家电商场为了解广告宣传费 x(万元)与营业额 y(万元)之间的关系,得到如下数据统计表:
广告宣传费 x(万元) 3 4 5 6 7
营业额 y(万元) 10 14 15 17 19
根据上表数据可得线性回归方程为 y=2. 1x+a,则 a 的值为
A. 3. 4 B. 5. 1 C. 2. 6 D. 4. 5
府谷三中高二数学(文科)期中试题- 2-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
第Ⅱ卷(非选择题 共 90 分)
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 命题“若 x>1,则 x>0”的否命题是 命题. (填“真”或“假”)
14. 根据多年气象统计资料,某地在节气夏至当日下雨的概率为 0. 45,阴天的概率为 0. 20,则
该地在节气夏至当日为晴天的概率为 .
15. “ x∈R,x2-2x-a≥0” 为真命题,则实数 a 的最大值为
16. 设有下列四个命题:
p1:直线 l 上有两点到平面 α 的距离相等,则 l∥α;
p2:垂直于同一条直线的两个平面平行;
p3:平行于同一条直线的两个平面平行.
则下列命题中所有真命题的序号为 .
①¬ p1∧p2 ②p1∧p3 ③ ¬ p2∨p3 ④¬ p3∨¬ p1
三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤)
17. (本小题满分 10 分)
为了适应新高考改革,某校组织了一次新高考质量测评,在成绩统计分析中,抽取了 12 名学生的成
绩,如图中茎叶图所示,学校规定测试成绩低于 87 分的为“未达标”,分数不低于 87 分的为“达标”.
(Ⅰ)求这组数据的众数和平均数;
(Ⅱ)若该校有 1 500 名学生参加了此次考试,估计成绩“达标”的学生
人数.
(第 17 题图)
18. (本小题满分 12 分)
已知集合 A={x a(Ⅰ)若 1∈A,求实数 a 的取值范围;
(Ⅱ)若 A≠ ,且 p 是 q 的充分不必要条件,求实数 a 的取值范围.
19. (本小题满分 12 分)
某快递公司招聘快递骑手,该公司提供了两种日工资方案:方案 1:规定每日底薪 50 元,快递
骑手每完成一单业务提成 3 元;方案 2:规定每日底薪 150 元,快递业务的前 44 单没有提成,从第
45 单开始,每完成一单业务提成 5 元,该快递公司记录了每天骑手的人均业务量. 现随机抽取 100
天的数据,将样本数据分为[25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七
组,整理得到如图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中 a 的值;
府谷三中高二数学(文科)期中试题- 3-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
(Ⅱ)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案
的选择,并说明理由(同组中的每个数据用该组区间的中点值代替) .
(第 19 题图)
20. (本小题满分 12 分)
已知某校甲、乙、丙三个兴趣小组的学生人数分别为 36,24,12,现采用分层抽样的方法从中抽
取 6 人进行睡眠质量的调查.
(Ⅰ)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人
(Ⅱ)现从这 6 人中随机抽取 2 人做进一步的身体检查,求抽取的 2 人来自同一兴趣小组的
概率.
21. (本小题满分 12 分)
设命题 p:不等式 a2-5a-6>0 成立;命题 q:关于 x 的方程 x2+ax+1 =0 有两个不相等的负根.
(Ⅰ)若 p 是真命题,求实数 a 的取值范围;
(Ⅱ)若命题“p 或 q”为真命题、“p 且 q”为假命题,求实数 a 的取值范围.
22. (本小题满分 12 分)
国家大力提倡科技创新,某工厂为提升甲产品的市场竞争力,对生产技术进行创新改造,使甲
产品的生产节能降耗. 表格提供了节能降耗后甲产品的生产产量 x(吨)与相应的生产能耗 y(吨)
的几组对照数据.
x(吨) 4 5 6 7
y(吨) 2. 5 3 4 4. 5
(Ⅰ)请根据表中提供的数据,用最小二乘法求出 y 关于 x 的线性回归方程 y= bx+a;
(Ⅱ)已知该厂技术改造前生产 8 吨甲产品的生产能耗为 7 吨,试根据(Ⅰ)中求出的线性回归
方程,预测节能降耗后生产 8 吨甲产品的生产能耗比技术改造前降低了多少吨
n
∑xiyi-nx y
参考公式:b= i=1n ,a= y-bx.
∑x2 2
i=1 i
-nx
府谷三中高二数学(文科)期中试题- 4-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
府谷三中 2020 ~ 2021 学年度第一学期期中质量检测
高二数学(文科)试题参考答案及评分标准
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. C 2. A 3. A 4. B 5. D 6. D 7. C 8. B 9. A 10. C 11. A 12. D
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 假 14. 0. 35 15. -1 16. ①④
三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤)
17. 解:(Ⅰ)由茎叶图知,这组数据的众数为 86. …………………………………………………………… (2 分)
平均数为 1 ×(51+64+66+78+85+86×3+87×2+92+98)= 80. 5. …………………………………… (5 分)
12
(Ⅱ)由茎叶图知,12 名同学中成绩“达标”的有 4 人,
1 500× 4 =500(人),
12
故成绩“达标”的学生约有 500 人. ………………………………………………………………… (10 分)
18. 解:(Ⅰ)∵ A={x a{a<1∴ ,解得 a<-1,a2>1
即实数 a 的取值范围是(-∞ ,-1) . ………………………………………………………………… (6 分)
(Ⅱ)∵ A≠ ,∴ a1,
-
由x 4- <0,得 1={x 1∵ p 是 q 的充分不必要条件,
∴ A B,
{a>1∴ ,解得 1∴ 实数 a 的取值范围是(1,2] . …………………………………………………………………… (12 分)
19. 解:(Ⅰ)由频率分布直方图得(0. 005+0. 005+a+0. 03+a+0. 015+0. 005)×10 =1,
解得 a=0. 02. ………………………………………………………………………………………… (6 分)
(Ⅱ)快递公司人均每日完成快递数量的平均数是:
30×0. 05+40×0. 05+50×0. 2+60×0. 3+70×0. 2+80×0. 15+90×0. 05 =62.
方案 1 日工资为:50+62×3 =236,
方案 2 日工资为:150+(62-44)×5 =240>236.
∴ 骑手应选择方案 2. ……………………………………………………………………………… (12 分)
府谷三中高二数学(文科)期中试题-答案-1(共 2 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
20. 解:(Ⅰ)应从甲兴趣小组的学生中抽取:6× 36 =3(人), ……………………………………… (2 分)
36+24+12
从乙兴趣小组的学生中抽取:6× 24 =+ + 2(人), ……………………………………………… (4 分)36 24 12
从丙兴趣小组的学生中抽取:6× 12 =+ + 1(人) . ……………………………………………… (6 分)36 24 12
(Ⅱ)甲兴趣小组抽取的 3 人记为 A,B,C;
乙兴趣小组抽取的 2 人记为 a,b;
丙兴趣小组抽取的 1 人记为 Q,
现从这 6 人中随机抽取 2 人,所有基本事件为:AB,AC,Aa,Ab,AQ,BC,Ba,Bb,BQ,Ca,Cb,CQ,ab,aQ,
bQ,共 15 种,
而抽取的 2 人来自同一兴趣小组有 4 种,
∴ 抽取的 2 人来自同一兴趣小组的概率 P= 4 . ………………………………………………… (12 分)
15
21. 解:(Ⅰ)由 p 为真命题,即 a2-5a-6>0,
解得 a>6 或 a<-1.
∴ 实数 a 的取值范围是(-∞ ,-1)∪(6,+∞ ) ……………………………………………………… (6 分)
a2-4>0
(Ⅱ)若 q 为真,则{ ,解得 a>2.-a<0
∵ 命题“p 或 q”为真命题、“p 且 q”为假命题,则 p 与 q 一真一假.
a>6 或 a<-1
若 p 真 q 假,则{ ,得 a<-1;a≤2
{-1≤a≤6若 p 假 q 真,则 ,得 22
∴ 实数 a 的取值范围是(-∞ ,-1)∪(2,6] ……………………………………………………… (12 分)
22. 解:(Ⅰ)x= 1 ×(4+5+6+7)= 5. 5,y= 1 ×(2. 5+3+4+4. 5)= 3. 5,
4 4
4 4
∑xiyi =80. 5,∑x2i =126,i=1 i=1
n
∑xiyi-nx y
b= i=1 =80. 5-4×5. 5×3. 5n 2 =0. 7,
∑x2i -nx2 126
-4×5. 5
i=1
a= y-bx=3. 5-0. 7×5. 5 = -0. 35.
∴ 线性回归方程为 y=0. 7x-0. 35. ………………………………………………………………… (6 分)
(Ⅱ)取 x=8,得 y=0. 7×8-0. 35 =5. 25,
∵ 7-5. 25 =1. 75.
∴ 预测节能降耗后生产 8 吨甲产品的生产能耗比技术改造前降低 1. 75 吨. …………………… (12 分)
府谷三中高二数学(文科)期中试题-答案-2(共 2 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
高二数学(文科)试题
注意事项:
1. 本试题共 4 页,满分 150 分,时间 120 分钟;
2. 答卷前,考生需准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准考证号;
3. 第Ⅰ卷选择题必须使用 2B 铅笔填涂,第Ⅱ卷非选择题必须使用 0. 5 毫米黑色墨水签字笔书
写,涂写要工整、清晰;
4. 考试结束后,监考员将答题卡按顺序收回,装袋整理;试题卷不回收。
第Ⅰ卷(选择题 共 60 分)
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合
题目要求的)
1. 为了解一批灯泡的使用寿命,从中抽取 20 只灯泡进行测试,在这个问题中,被抽取的 20 只
灯泡的使用寿命是
A. 总体 B. 个体 C. 样本 D. 样本容量
2. 在下列各图中,变量 x,y 具有线性相关关系的是
3. 命题“ x>0,ln x>0”的否定为
A. x>0,ln x≤0 B. x≤0,ln x≤0 C. x>0,ln x<0 D. x>0,ln x≤0
4. 某会场有 28 排,每排有 32 个座位,在一次报告中恰好坐满了听众,报告结束后,为了了解听
众意见,需要抽取 28 名听众进行座谈,则最合理的抽样方法是
A. 抽签法 B. 系统抽样法 C. 分层抽样法 D. 随机数表法
5. 下列命题中是假命题的是
A. x0∈R,lg x0 =0 B. x0∈R,tan x0 =0
C. x∈R,3x>0 D. x∈R,x2>0
6. 为了解某地区九年级男生的身高情况,随机选取了该地区 100 名九年级男生进行测量,他们
的身高 x(cm)统计如下表:
组别(cm) x≤160 160
人数 15 42 38 5
府谷三中高二数学(文科)期中试题- 1-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
根据上表,抽查该地区一名九年级男生,估计他的身高不高于 180 cm 的概率是
A. 0. 05 B. 0. 38 C. 0. 57 D. 0. 95
7. 已知偶函数 f(x)在[0,+∞ )上单调递增,则对实数 a,b,“ a > b ”是“ f(a)>f(b)”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
8. 边长为 m 的正方形内有一个半径为 n(n
视为质点),若它落在该圆内的概率为 1 ,则圆周率 π 的值为
2
A. m B. m
2
C. n D. n
2
2n 2n2 2m 2m2
9. 有一组 8 个数字的数据组,其平均数为 5,方差为 3. 现给该数据组增加一个数字 5,此时这 9
个数字的平均数为 x,方差为 s2,则
A. x=5,s2<3 B. x>5,s2<3 C. x=5,s2>3 D. x>5,s2>3
10. 如图是某地某月 1 日至 15 日的日平均温度变化的折线图,则下列结论正确的是
(第 10 题图)
A. 这 15 天日平均温度的极差为 15 ℃
B. 由折线图能预测 16 日的日平均温度要低于 19 ℃
C. 连续三天日平均温度的方差最大的是 7 日,8 日,9 日三天
D. 由折线图能预测本月的日平均温度小于 25 ℃的天数少于日平均温度大于 25 ℃的天数
11. 已知函数 f(x)= 2ax-a+3,若 x0∈(-1,1),使得 f(x0)= 0,则实数 a 的取值范围是
A. (-∞ ,-3)∪(1,+∞ ) B. (-∞ ,-3)
C. (-3,1) D. (1,+∞ )
12. 某家电商场为了解广告宣传费 x(万元)与营业额 y(万元)之间的关系,得到如下数据统计表:
广告宣传费 x(万元) 3 4 5 6 7
营业额 y(万元) 10 14 15 17 19
根据上表数据可得线性回归方程为 y=2. 1x+a,则 a 的值为
A. 3. 4 B. 5. 1 C. 2. 6 D. 4. 5
府谷三中高二数学(文科)期中试题- 2-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
第Ⅱ卷(非选择题 共 90 分)
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 命题“若 x>1,则 x>0”的否命题是 命题. (填“真”或“假”)
14. 根据多年气象统计资料,某地在节气夏至当日下雨的概率为 0. 45,阴天的概率为 0. 20,则
该地在节气夏至当日为晴天的概率为 .
15. “ x∈R,x2-2x-a≥0” 为真命题,则实数 a 的最大值为
16. 设有下列四个命题:
p1:直线 l 上有两点到平面 α 的距离相等,则 l∥α;
p2:垂直于同一条直线的两个平面平行;
p3:平行于同一条直线的两个平面平行.
则下列命题中所有真命题的序号为 .
①¬ p1∧p2 ②p1∧p3 ③ ¬ p2∨p3 ④¬ p3∨¬ p1
三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤)
17. (本小题满分 10 分)
为了适应新高考改革,某校组织了一次新高考质量测评,在成绩统计分析中,抽取了 12 名学生的成
绩,如图中茎叶图所示,学校规定测试成绩低于 87 分的为“未达标”,分数不低于 87 分的为“达标”.
(Ⅰ)求这组数据的众数和平均数;
(Ⅱ)若该校有 1 500 名学生参加了此次考试,估计成绩“达标”的学生
人数.
(第 17 题图)
18. (本小题满分 12 分)
已知集合 A={x a
(Ⅱ)若 A≠ ,且 p 是 q 的充分不必要条件,求实数 a 的取值范围.
19. (本小题满分 12 分)
某快递公司招聘快递骑手,该公司提供了两种日工资方案:方案 1:规定每日底薪 50 元,快递
骑手每完成一单业务提成 3 元;方案 2:规定每日底薪 150 元,快递业务的前 44 单没有提成,从第
45 单开始,每完成一单业务提成 5 元,该快递公司记录了每天骑手的人均业务量. 现随机抽取 100
天的数据,将样本数据分为[25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七
组,整理得到如图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中 a 的值;
府谷三中高二数学(文科)期中试题- 3-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
(Ⅱ)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案
的选择,并说明理由(同组中的每个数据用该组区间的中点值代替) .
(第 19 题图)
20. (本小题满分 12 分)
已知某校甲、乙、丙三个兴趣小组的学生人数分别为 36,24,12,现采用分层抽样的方法从中抽
取 6 人进行睡眠质量的调查.
(Ⅰ)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人
(Ⅱ)现从这 6 人中随机抽取 2 人做进一步的身体检查,求抽取的 2 人来自同一兴趣小组的
概率.
21. (本小题满分 12 分)
设命题 p:不等式 a2-5a-6>0 成立;命题 q:关于 x 的方程 x2+ax+1 =0 有两个不相等的负根.
(Ⅰ)若 p 是真命题,求实数 a 的取值范围;
(Ⅱ)若命题“p 或 q”为真命题、“p 且 q”为假命题,求实数 a 的取值范围.
22. (本小题满分 12 分)
国家大力提倡科技创新,某工厂为提升甲产品的市场竞争力,对生产技术进行创新改造,使甲
产品的生产节能降耗. 表格提供了节能降耗后甲产品的生产产量 x(吨)与相应的生产能耗 y(吨)
的几组对照数据.
x(吨) 4 5 6 7
y(吨) 2. 5 3 4 4. 5
(Ⅰ)请根据表中提供的数据,用最小二乘法求出 y 关于 x 的线性回归方程 y= bx+a;
(Ⅱ)已知该厂技术改造前生产 8 吨甲产品的生产能耗为 7 吨,试根据(Ⅰ)中求出的线性回归
方程,预测节能降耗后生产 8 吨甲产品的生产能耗比技术改造前降低了多少吨
n
∑xiyi-nx y
参考公式:b= i=1n ,a= y-bx.
∑x2 2
i=1 i
-nx
府谷三中高二数学(文科)期中试题- 4-(共 4 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
府谷三中 2020 ~ 2021 学年度第一学期期中质量检测
高二数学(文科)试题参考答案及评分标准
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. C 2. A 3. A 4. B 5. D 6. D 7. C 8. B 9. A 10. C 11. A 12. D
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 假 14. 0. 35 15. -1 16. ①④
三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤)
17. 解:(Ⅰ)由茎叶图知,这组数据的众数为 86. …………………………………………………………… (2 分)
平均数为 1 ×(51+64+66+78+85+86×3+87×2+92+98)= 80. 5. …………………………………… (5 分)
12
(Ⅱ)由茎叶图知,12 名同学中成绩“达标”的有 4 人,
1 500× 4 =500(人),
12
故成绩“达标”的学生约有 500 人. ………………………………………………………………… (10 分)
18. 解:(Ⅰ)∵ A={x a
即实数 a 的取值范围是(-∞ ,-1) . ………………………………………………………………… (6 分)
(Ⅱ)∵ A≠ ,∴ a
-
由x 4- <0,得 1
∴ A B,
{a>1∴ ,解得 1
19. 解:(Ⅰ)由频率分布直方图得(0. 005+0. 005+a+0. 03+a+0. 015+0. 005)×10 =1,
解得 a=0. 02. ………………………………………………………………………………………… (6 分)
(Ⅱ)快递公司人均每日完成快递数量的平均数是:
30×0. 05+40×0. 05+50×0. 2+60×0. 3+70×0. 2+80×0. 15+90×0. 05 =62.
方案 1 日工资为:50+62×3 =236,
方案 2 日工资为:150+(62-44)×5 =240>236.
∴ 骑手应选择方案 2. ……………………………………………………………………………… (12 分)
府谷三中高二数学(文科)期中试题-答案-1(共 2 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
20. 解:(Ⅰ)应从甲兴趣小组的学生中抽取:6× 36 =3(人), ……………………………………… (2 分)
36+24+12
从乙兴趣小组的学生中抽取:6× 24 =+ + 2(人), ……………………………………………… (4 分)36 24 12
从丙兴趣小组的学生中抽取:6× 12 =+ + 1(人) . ……………………………………………… (6 分)36 24 12
(Ⅱ)甲兴趣小组抽取的 3 人记为 A,B,C;
乙兴趣小组抽取的 2 人记为 a,b;
丙兴趣小组抽取的 1 人记为 Q,
现从这 6 人中随机抽取 2 人,所有基本事件为:AB,AC,Aa,Ab,AQ,BC,Ba,Bb,BQ,Ca,Cb,CQ,ab,aQ,
bQ,共 15 种,
而抽取的 2 人来自同一兴趣小组有 4 种,
∴ 抽取的 2 人来自同一兴趣小组的概率 P= 4 . ………………………………………………… (12 分)
15
21. 解:(Ⅰ)由 p 为真命题,即 a2-5a-6>0,
解得 a>6 或 a<-1.
∴ 实数 a 的取值范围是(-∞ ,-1)∪(6,+∞ ) ……………………………………………………… (6 分)
a2-4>0
(Ⅱ)若 q 为真,则{ ,解得 a>2.-a<0
∵ 命题“p 或 q”为真命题、“p 且 q”为假命题,则 p 与 q 一真一假.
a>6 或 a<-1
若 p 真 q 假,则{ ,得 a<-1;a≤2
{-1≤a≤6若 p 假 q 真,则 ,得 2
∴ 实数 a 的取值范围是(-∞ ,-1)∪(2,6] ……………………………………………………… (12 分)
22. 解:(Ⅰ)x= 1 ×(4+5+6+7)= 5. 5,y= 1 ×(2. 5+3+4+4. 5)= 3. 5,
4 4
4 4
∑xiyi =80. 5,∑x2i =126,i=1 i=1
n
∑xiyi-nx y
b= i=1 =80. 5-4×5. 5×3. 5n 2 =0. 7,
∑x2i -nx2 126
-4×5. 5
i=1
a= y-bx=3. 5-0. 7×5. 5 = -0. 35.
∴ 线性回归方程为 y=0. 7x-0. 35. ………………………………………………………………… (6 分)
(Ⅱ)取 x=8,得 y=0. 7×8-0. 35 =5. 25,
∵ 7-5. 25 =1. 75.
∴ 预测节能降耗后生产 8 吨甲产品的生产能耗比技术改造前降低 1. 75 吨. …………………… (12 分)
府谷三中高二数学(文科)期中试题-答案-2(共 2 页)
{#{QQABIQIEogggAAJAARgCQQFgCECQkAGCAIgGRAAMIAIASQFABAA=}#}
同课章节目录
