不等式及其解集[下学期]
图片预览






文档简介
课件14张PPT。9.1.1 不 等 式及其解集 今年“五一黄金周”,某中学组织部分学生去桃渚古城开展团队活动,桃渚古城的票价是:每人5元;一次购票满30张.每张票可少收1元。共有27名同学报名参加此次活动.当领队王老师准备去售票处买27张票时,爱动脑筋的李敏同学喊住了王老师,提议买30张票.但有的同学不明白,明明我们只有27人,买30张票,岂不是“浪费”吗?那么,究竟李敏的提议对不对呢?是不是真的“浪费”呢?总结:像上面出现的这样用">"或"<"等不等号表示不等关系的式子,叫做不等式.方案一:买27张票 27×5=135(元)方案二:买30张票 30×4=120(元)120﹤135所以李敏同学的提议是正确的.情景引入“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号判判断下列各式是不是不等式。
2﹤5; ② x+3≠0;
③ 4x-2y≤0 ; ④ 7n-5≥2;
⑤3x2+2>0 ; ⑥ 5m+3=8 。归纳:像②、④这样,只含有一个未知数,且未知数的次数都是1的不等式,叫作一元一次不等式。火眼金睛否是是是是是思 考:若3x3m-1+2<4是一元一次不等式,则m的值为______.你能举出几个一元一次不等式吗?用不等式表示下列数量关系:
(1)x的一半小于-1;
(2)a是负数;
(3)x与y的差不大于-2;
(4)a的4倍大于或等于8 ;
(5)b是非负数;
(6)x与2的和大于5。 大显身手 当然如果去桃渚古城的人数较少(比如10个人),显然不值得去买30张票,还是按实际人数买票为好.现在的问题是:小于30人时,至少要有多少人去桃渚古城,买30张票反而合算呢?
解:设有x(x<30)人要去桃渚古城.那么按实际人数买票x张,需付款5x(元)买30张票需付款4×30=120(元)如果买30张票合算,那么应有:120<5x深入探究思考:你能发现当有多少人去时买30张票合算吗?当x取哪些值时,120<5x才成立呢? x
5x
比较120与5x的大小
120<5x成立吗?
21
105
120>5x
不成立
22
110
120>5x
不成立
23
115
120>5x
不成立
24
120
120=5x
不成立
25
125
120<5x
成立
26
130
120<5x
成立
27
135
120<5x
成立
28
140
120<5x
成立
29
145
120<5x
成立
填表探究
当x取25、26、27、28、29时不等120<5x成立, 能使不等式成立的未知数的值,叫做不等式的解。
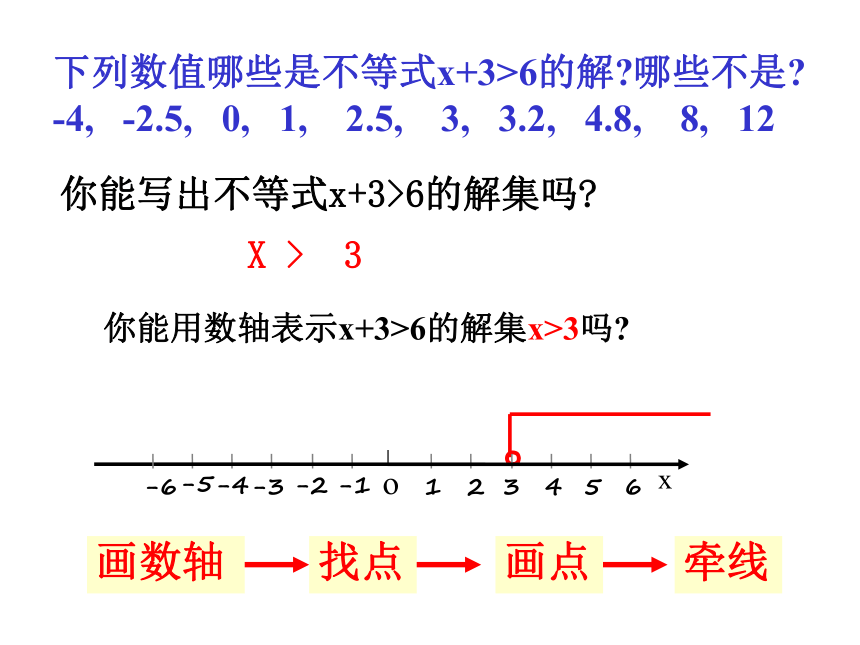
思考:你还能找出这个不等式的其它解吗?这个不等式有多少个解?当x>24时,不等式总成立.无数个解 使不等式成立的未知数的取值范围,叫做不等式的解集。你能说出不等式的解与不等式的解集的区别吗?下列数值哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 2.5, 3, 3.2, 4.8, 8, 12你能写出不等式x+3>6的解集吗?X > 3画数轴找点画点牵线你能用数轴表示x+3>6的解集x>3吗?。Bx<2x>2x≤2x≥22、图中红色部分所表示的是哪些数?你能用不等式表示这个区域吗?0-113、请说出一个不等式,使得3是它的一个解,而4不是它的解。X<14.聪明的你能说出下列不等式的解集吗?
并把解集表示在数轴上。
(1)2x≤8 ;
(2)x+3<0;
(3)x-2≥0努力探究5.如何在数轴上表示:-2 < y ≤3 ?燃放某种烟花时,为了确保安全,人在点燃导火线后要在燃放前转移到10m外的安全区域。已知导火线的燃烧速度为0.02m/s,人离开的速度为4m/s,那么导火线的长度应为多少米?
解:设导火线的长度为x米。应用生活这节课“我学会了......”1.不等式的概念.2.一元一次不等式的概念.3.不等式的解及其解集.4.用不等式表示生活中数量关系.5.生活中不等关系无处不在.课堂感悟 课后思考题:我们班如果要组织同学去桃渚古城开展活动,该如何买票更加合算?(桃渚古城的票价是:每人5元;一次购票满30张,每张票可少收1元。)
2﹤5; ② x+3≠0;
③ 4x-2y≤0 ; ④ 7n-5≥2;
⑤3x2+2>0 ; ⑥ 5m+3=8 。归纳:像②、④这样,只含有一个未知数,且未知数的次数都是1的不等式,叫作一元一次不等式。火眼金睛否是是是是是思 考:若3x3m-1+2<4是一元一次不等式,则m的值为______.你能举出几个一元一次不等式吗?用不等式表示下列数量关系:
(1)x的一半小于-1;
(2)a是负数;
(3)x与y的差不大于-2;
(4)a的4倍大于或等于8 ;
(5)b是非负数;
(6)x与2的和大于5。 大显身手 当然如果去桃渚古城的人数较少(比如10个人),显然不值得去买30张票,还是按实际人数买票为好.现在的问题是:小于30人时,至少要有多少人去桃渚古城,买30张票反而合算呢?
解:设有x(x<30)人要去桃渚古城.那么按实际人数买票x张,需付款5x(元)买30张票需付款4×30=120(元)如果买30张票合算,那么应有:120<5x深入探究思考:你能发现当有多少人去时买30张票合算吗?当x取哪些值时,120<5x才成立呢? x
5x
比较120与5x的大小
120<5x成立吗?
21
105
120>5x
不成立
22
110
120>5x
不成立
23
115
120>5x
不成立
24
120
120=5x
不成立
25
125
120<5x
成立
26
130
120<5x
成立
27
135
120<5x
成立
28
140
120<5x
成立
29
145
120<5x
成立
填表探究
当x取25、26、27、28、29时不等120<5x成立, 能使不等式成立的未知数的值,叫做不等式的解。
思考:你还能找出这个不等式的其它解吗?这个不等式有多少个解?当x>24时,不等式总成立.无数个解 使不等式成立的未知数的取值范围,叫做不等式的解集。你能说出不等式的解与不等式的解集的区别吗?下列数值哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 2.5, 3, 3.2, 4.8, 8, 12你能写出不等式x+3>6的解集吗?X > 3画数轴找点画点牵线你能用数轴表示x+3>6的解集x>3吗?。Bx<2x>2x≤2x≥22、图中红色部分所表示的是哪些数?你能用不等式表示这个区域吗?0-113、请说出一个不等式,使得3是它的一个解,而4不是它的解。X<14.聪明的你能说出下列不等式的解集吗?
并把解集表示在数轴上。
(1)2x≤8 ;
(2)x+3<0;
(3)x-2≥0努力探究5.如何在数轴上表示:-2 < y ≤3 ?燃放某种烟花时,为了确保安全,人在点燃导火线后要在燃放前转移到10m外的安全区域。已知导火线的燃烧速度为0.02m/s,人离开的速度为4m/s,那么导火线的长度应为多少米?
解:设导火线的长度为x米。应用生活这节课“我学会了......”1.不等式的概念.2.一元一次不等式的概念.3.不等式的解及其解集.4.用不等式表示生活中数量关系.5.生活中不等关系无处不在.课堂感悟 课后思考题:我们班如果要组织同学去桃渚古城开展活动,该如何买票更加合算?(桃渚古城的票价是:每人5元;一次购票满30张,每张票可少收1元。)
