2023年河南省平顶山市部分地区模拟预测数学试题(无答案)
文档属性
| 名称 | 2023年河南省平顶山市部分地区模拟预测数学试题(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 821.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览

文档简介
数学试卷
注意事项:
1.本试卷分试题卷和答题卷两部分.试题卷共6页,3大题,满分120分,考试时间100分钟.
2.试题卷上不要答题,选择题用2B铅笔按要求填涂在答题卷上的指定位置,非选择题请用0.5毫米黑色签字笔直接把答案写在答题卷上,答在试题卷上的答案无效.
3.答题前,考生务必将本人所在学校、姓名、考场、座号和准考证号填写在答题卷第一面的指定位置上.
一、选择题(每小题3分,共30分)
下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内.
1.下列各数中,绝对值最大的数是( )
A.3 B.0 C. D.
2.据光明网消息,我国2022年全国粮食总产量达13731亿斤,再创历史新高,将数据“13731亿”用科学记数法表示为( )
A. B. C. D.
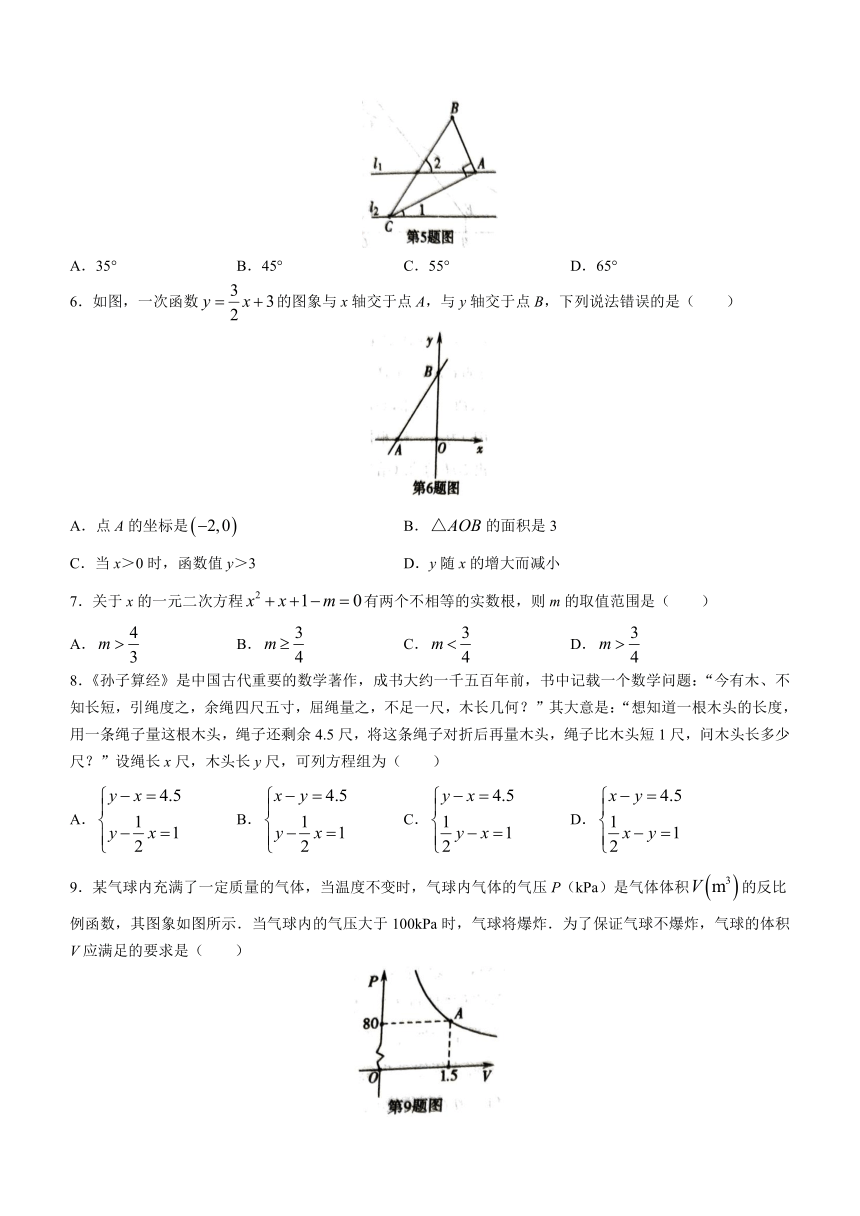
3.如图所示的几何体的俯视图是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.如图,直线,中,∠B=60°,直角顶点A在直线上,顶点C在直线上,已知∠1=25°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
6.如图,一次函数的图象与x轴交于点A,与y轴交于点B,下列说法错误的是( )
A.点A的坐标是 B.的面积是3
C.当x>0时,函数值y>3 D.y随x的增大而减小
7.关于x的一元二次方程有两个不相等的实数根,则m的取值范围是( )
A. B. C. D.
8.《孙子算经》是中国古代重要的数学著作,成书大约一千五百年前,书中记载一个数学问题:“今有木、不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?”其大意是:“想知道一根木头的长度,用一条绳子量这根木头,绳子还剩余4.5尺,将这条绳子对折后再量木头,绳子比木头短1尺,问木头长多少尺?”设绳长x尺,木头长y尺,可列方程组为( )
A. B. C. D.
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积的反比例函数,其图象如图所示.当气球内的气压大于100kPa时,气球将爆炸.为了保证气球不爆炸,气球的体积V应满足的要求是( )
A. B. C. D.
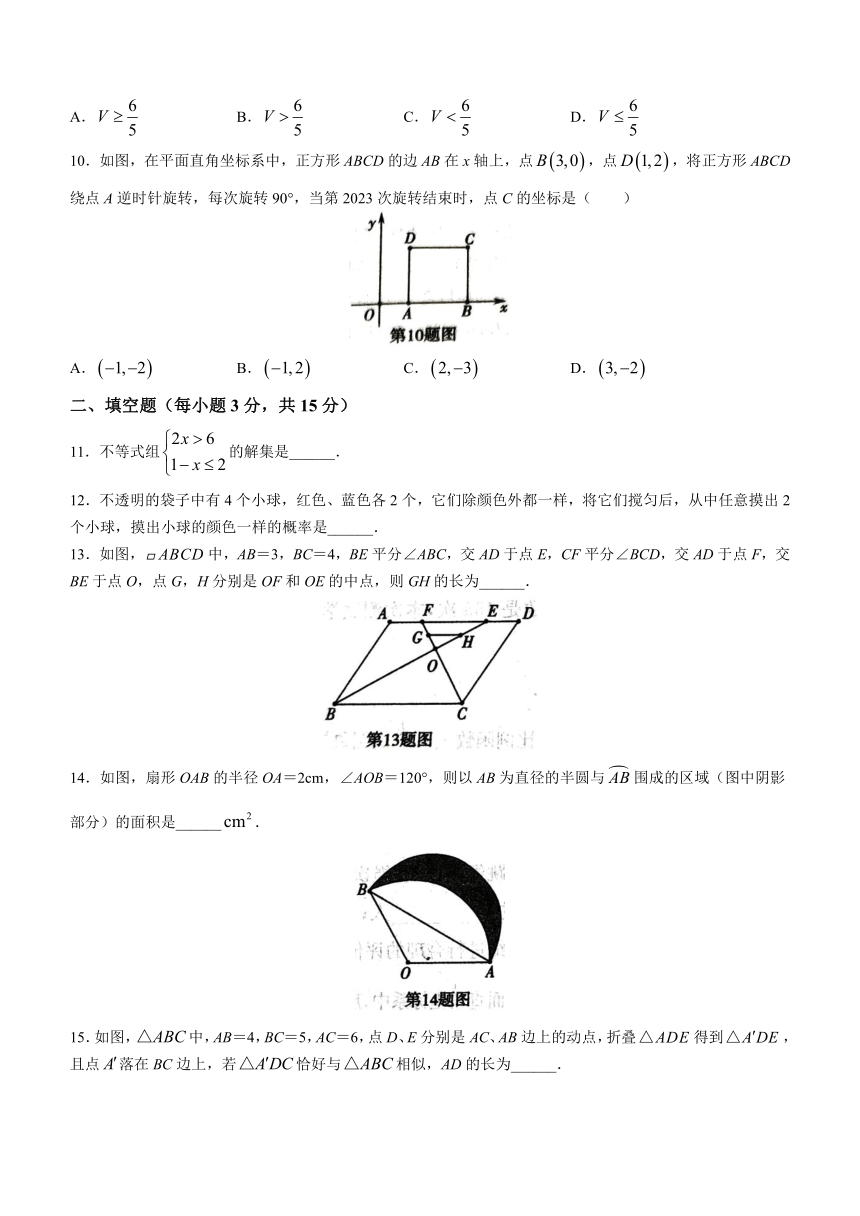
10.如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点,点,将正方形ABCD绕点A逆时针旋转,每次旋转90°,当第2023次旋转结束时,点C的坐标是( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.不等式组的解集是______.
12.不透明的袋子中有4个小球,红色、蓝色各2个,它们除颜色外都一样,将它们搅匀后,从中任意摸出2个小球,摸出小球的颜色一样的概率是______.
13.如图,中,AB=3,BC=4,BE平分∠ABC,交AD于点E,CF平分∠BCD,交AD于点F,交BE于点O,点G,H分别是OF和OE的中点,则GH的长为______.
14.如图,扇形OAB的半径OA=2cm,∠AOB=120°,则以AB为直径的半圆与围成的区域(图中阴影部分)的面积是______.
15.如图,中,AB=4,BC=5,AC=6,点D、E分别是AC、AB边上的动点,折叠得到,且点落在BC边上,若恰好与相似,AD的长为______.
三、解答题(本大题共8个小题,满分75分)
16.(10分)(1)计算:;
(2)化简:.
17.(9分)跳绳是普及性很好的体育运动项目,在我国有着非常悠久的历史,这种运动唐朝称“透索”,宋称“跳索”,明称“跳百索”、“跳白索”、“跳马索”,清称“绳飞”,清末以后称作“跳绳”.某中学把跳绳作为学校特色体育运动项目之一.2023年4月份,为了了解八年级学生每分钟跳绳次数,该校随机抽取了八年级50名学生,进行一分钟跳绳测试,并将测试成绩(满分为10分)进行整理,绘制了如下统计表.
调查结果统计表①
组别 每分钟跳绳数x(次) 成绩(分) 频数(人)
A 5 2
B 6 5
C 7 8
D 8 9
E 9 15
F 10 11
规定:得10分为优秀,达到8分为良好,达到6分为合格.
调查结果统计表②
D组跳绳 次数统计: 140,145,145, 147,155,155, 155,156,158.
根据以上信息解答下列问题:
(1)在这次测试中,成绩的众数是______分;
(2)参与测试的学生中获得良好及以上等级的学生占测试人数的百分比是______;
(3)王莉参加了这次跳绳测试,跳绳次数是155次,本次测试学生中比她的跳绳次数少的是______人;
(4)请对本次测试成绩进行合理的评价.
18.(9分)如图,在平面直角坐标系中,反比例函数的图象与一次函数的图象交于点B和C,与一次函数的图象交于点A和B,点B的纵坐标是6,点C的横坐标是3.
(1求反比例函数和直线BC的解析式;
(2)填空:①当时,x的取值范围是______;②当时,x的取值范围是______.
19.(9分)如图所示,为了知道楼房CP外墙上一广告屏的高度GH是多少,某数学活动小组利用测角仪和米尺等工具进行如下操作:在A处测得∠GDF=30°,在B处测得∠HEF=50°,点A、B、C共线,于点C,于点F,AB为20米,BC=30米,测角仪的高度(AD、BE)为1.3米.根据测量数据,请求出GH的值.(结果精确到0.1米,参考数据:,,,)
20.(9分)如图,隧道的截面由抛物线BEC和矩形ABCD构成,矩形的长AD为8m,宽AB为2m.以AD所在直线为x轴,线段AD的中垂线为y轴,建立平面直角坐标系,抛物线顶点E到坐标原点O的距离为5m.
(1)求这条抛物线的解析式;
(2)如果隧道是双向通道,现有一辆货车高3.6m,宽2.4m,这辆货车能否通过该隧道?请通过计算进行说明.
21.(9分)为创建宜居环境,某市正在建设若干街心花园,某工程队负责在街心花园种植A、B两种树木,已知A种树木的单价比B种树木的单价贵20元.工程队在第一批购买中,购买A树木花费2400元,购买B树木花费1200元,且所购买A树木的数量是B树木的数量的1.5倍.
(1)求第一批购买时,A、B两种树木的单价各是多少元?
(2)工程队计划第二批购买A、B两种树木的总数量是第一批总数量的2倍,此次购买时两种树木的单价没有变化,本次购买预算总费用不超过7200元,A种树苗最多可以购买多少棵?
22.(10分)如图,在中,∠BAC=90°,AB=4,AC=6,点O在边AB上,以OB为半径作,交BC于点D,连接OD.
(1)尺规作图:先作线段CD的垂直平分线l,交AC于点E,再作直线DE;(要求:不写作法,保留作图痕迹,使用2B铅笔)
(2)DE是的切线吗?请说明理由;
(3)当点O是AB中点时,请直接写出此时线段DE的长.
23.(10分)综合与实践
综合与实践课上,老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动.
(1)操作判断
如图1,先用对折的方式确定矩形ABCD的边AB的中点E,再沿DE折叠,点A落在点F处,把纸片展平,延长DF,与BC交点为G.
请写出线段FG与线段BG的数量关系______.
(2)迁移思考
如图2,把按照(1)中的操作进行折叠和作图,请判断FG,BG这两条线段之间的数量关系,并仅就图2证明你的判断.
(3)拓展探索
如图1,若AB=2,按照(1)中的操作进行折叠和作图,请直接写出当CG=1时AD的值.
注意事项:
1.本试卷分试题卷和答题卷两部分.试题卷共6页,3大题,满分120分,考试时间100分钟.
2.试题卷上不要答题,选择题用2B铅笔按要求填涂在答题卷上的指定位置,非选择题请用0.5毫米黑色签字笔直接把答案写在答题卷上,答在试题卷上的答案无效.
3.答题前,考生务必将本人所在学校、姓名、考场、座号和准考证号填写在答题卷第一面的指定位置上.
一、选择题(每小题3分,共30分)
下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内.
1.下列各数中,绝对值最大的数是( )
A.3 B.0 C. D.
2.据光明网消息,我国2022年全国粮食总产量达13731亿斤,再创历史新高,将数据“13731亿”用科学记数法表示为( )
A. B. C. D.
3.如图所示的几何体的俯视图是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.如图,直线,中,∠B=60°,直角顶点A在直线上,顶点C在直线上,已知∠1=25°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
6.如图,一次函数的图象与x轴交于点A,与y轴交于点B,下列说法错误的是( )
A.点A的坐标是 B.的面积是3
C.当x>0时,函数值y>3 D.y随x的增大而减小
7.关于x的一元二次方程有两个不相等的实数根,则m的取值范围是( )
A. B. C. D.
8.《孙子算经》是中国古代重要的数学著作,成书大约一千五百年前,书中记载一个数学问题:“今有木、不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?”其大意是:“想知道一根木头的长度,用一条绳子量这根木头,绳子还剩余4.5尺,将这条绳子对折后再量木头,绳子比木头短1尺,问木头长多少尺?”设绳长x尺,木头长y尺,可列方程组为( )
A. B. C. D.
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积的反比例函数,其图象如图所示.当气球内的气压大于100kPa时,气球将爆炸.为了保证气球不爆炸,气球的体积V应满足的要求是( )
A. B. C. D.
10.如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点,点,将正方形ABCD绕点A逆时针旋转,每次旋转90°,当第2023次旋转结束时,点C的坐标是( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.不等式组的解集是______.
12.不透明的袋子中有4个小球,红色、蓝色各2个,它们除颜色外都一样,将它们搅匀后,从中任意摸出2个小球,摸出小球的颜色一样的概率是______.
13.如图,中,AB=3,BC=4,BE平分∠ABC,交AD于点E,CF平分∠BCD,交AD于点F,交BE于点O,点G,H分别是OF和OE的中点,则GH的长为______.
14.如图,扇形OAB的半径OA=2cm,∠AOB=120°,则以AB为直径的半圆与围成的区域(图中阴影部分)的面积是______.
15.如图,中,AB=4,BC=5,AC=6,点D、E分别是AC、AB边上的动点,折叠得到,且点落在BC边上,若恰好与相似,AD的长为______.
三、解答题(本大题共8个小题,满分75分)
16.(10分)(1)计算:;
(2)化简:.
17.(9分)跳绳是普及性很好的体育运动项目,在我国有着非常悠久的历史,这种运动唐朝称“透索”,宋称“跳索”,明称“跳百索”、“跳白索”、“跳马索”,清称“绳飞”,清末以后称作“跳绳”.某中学把跳绳作为学校特色体育运动项目之一.2023年4月份,为了了解八年级学生每分钟跳绳次数,该校随机抽取了八年级50名学生,进行一分钟跳绳测试,并将测试成绩(满分为10分)进行整理,绘制了如下统计表.
调查结果统计表①
组别 每分钟跳绳数x(次) 成绩(分) 频数(人)
A 5 2
B 6 5
C 7 8
D 8 9
E 9 15
F 10 11
规定:得10分为优秀,达到8分为良好,达到6分为合格.
调查结果统计表②
D组跳绳 次数统计: 140,145,145, 147,155,155, 155,156,158.
根据以上信息解答下列问题:
(1)在这次测试中,成绩的众数是______分;
(2)参与测试的学生中获得良好及以上等级的学生占测试人数的百分比是______;
(3)王莉参加了这次跳绳测试,跳绳次数是155次,本次测试学生中比她的跳绳次数少的是______人;
(4)请对本次测试成绩进行合理的评价.
18.(9分)如图,在平面直角坐标系中,反比例函数的图象与一次函数的图象交于点B和C,与一次函数的图象交于点A和B,点B的纵坐标是6,点C的横坐标是3.
(1求反比例函数和直线BC的解析式;
(2)填空:①当时,x的取值范围是______;②当时,x的取值范围是______.
19.(9分)如图所示,为了知道楼房CP外墙上一广告屏的高度GH是多少,某数学活动小组利用测角仪和米尺等工具进行如下操作:在A处测得∠GDF=30°,在B处测得∠HEF=50°,点A、B、C共线,于点C,于点F,AB为20米,BC=30米,测角仪的高度(AD、BE)为1.3米.根据测量数据,请求出GH的值.(结果精确到0.1米,参考数据:,,,)
20.(9分)如图,隧道的截面由抛物线BEC和矩形ABCD构成,矩形的长AD为8m,宽AB为2m.以AD所在直线为x轴,线段AD的中垂线为y轴,建立平面直角坐标系,抛物线顶点E到坐标原点O的距离为5m.
(1)求这条抛物线的解析式;
(2)如果隧道是双向通道,现有一辆货车高3.6m,宽2.4m,这辆货车能否通过该隧道?请通过计算进行说明.
21.(9分)为创建宜居环境,某市正在建设若干街心花园,某工程队负责在街心花园种植A、B两种树木,已知A种树木的单价比B种树木的单价贵20元.工程队在第一批购买中,购买A树木花费2400元,购买B树木花费1200元,且所购买A树木的数量是B树木的数量的1.5倍.
(1)求第一批购买时,A、B两种树木的单价各是多少元?
(2)工程队计划第二批购买A、B两种树木的总数量是第一批总数量的2倍,此次购买时两种树木的单价没有变化,本次购买预算总费用不超过7200元,A种树苗最多可以购买多少棵?
22.(10分)如图,在中,∠BAC=90°,AB=4,AC=6,点O在边AB上,以OB为半径作,交BC于点D,连接OD.
(1)尺规作图:先作线段CD的垂直平分线l,交AC于点E,再作直线DE;(要求:不写作法,保留作图痕迹,使用2B铅笔)
(2)DE是的切线吗?请说明理由;
(3)当点O是AB中点时,请直接写出此时线段DE的长.
23.(10分)综合与实践
综合与实践课上,老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动.
(1)操作判断
如图1,先用对折的方式确定矩形ABCD的边AB的中点E,再沿DE折叠,点A落在点F处,把纸片展平,延长DF,与BC交点为G.
请写出线段FG与线段BG的数量关系______.
(2)迁移思考
如图2,把按照(1)中的操作进行折叠和作图,请判断FG,BG这两条线段之间的数量关系,并仅就图2证明你的判断.
(3)拓展探索
如图1,若AB=2,按照(1)中的操作进行折叠和作图,请直接写出当CG=1时AD的值.
同课章节目录
