24.1.2 垂直于弦的直径 提高卷 2023-2024学年人教版九年级数学上册(含答案)
文档属性
| 名称 | 24.1.2 垂直于弦的直径 提高卷 2023-2024学年人教版九年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 687.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览


文档简介
24.1.2 垂直于弦的直径 提高卷
一、单选题
1.如图是小明完成的.作法是:取的直径,在上任取一点引弦当点在半圆上移动时点不与A、B重合,的平分线与的交点必( )
A.平分弧 B.三等分弧
C.到点和直径的距离相等 D.到点和点的距离相等
2.如图,的直径,是的弦,,垂足为M,,则的长为( )
A.8 B.12 C.16 D.
3.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则的半径为( )
A.13cm B.16cm C.26cm D.20cm
4.已知△ABC的边BC= ,且△ABC内接于半径为2的⊙O,则∠A的度数是( )
A.60° B.120° C.60°或120° D.90°
5.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
A.1 B.1.5 C.2 D.2.5
6.已知AB、CD是⊙O的两条弦,AB∥CD,AB=6,CD=8,⊙O的半径为5,则AB与CD的距离是( )
A.1 B.7 C.1或7 D.无法确定
7.如图,在半圆中,直径,是半圆上一点,将弧沿弦折叠交于,点是弧的中点.连接,则的最小值为( )
A. B. C. D.
8.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3)
C.点(5,1) D.点(6,1)
二、填空题
9.如图,在半径为5的中,半径与弦垂直,垂足为点D,且,则的长等于 .
10.如图,在中,点是的中点,连接交弦于点,若,,则的长是 .
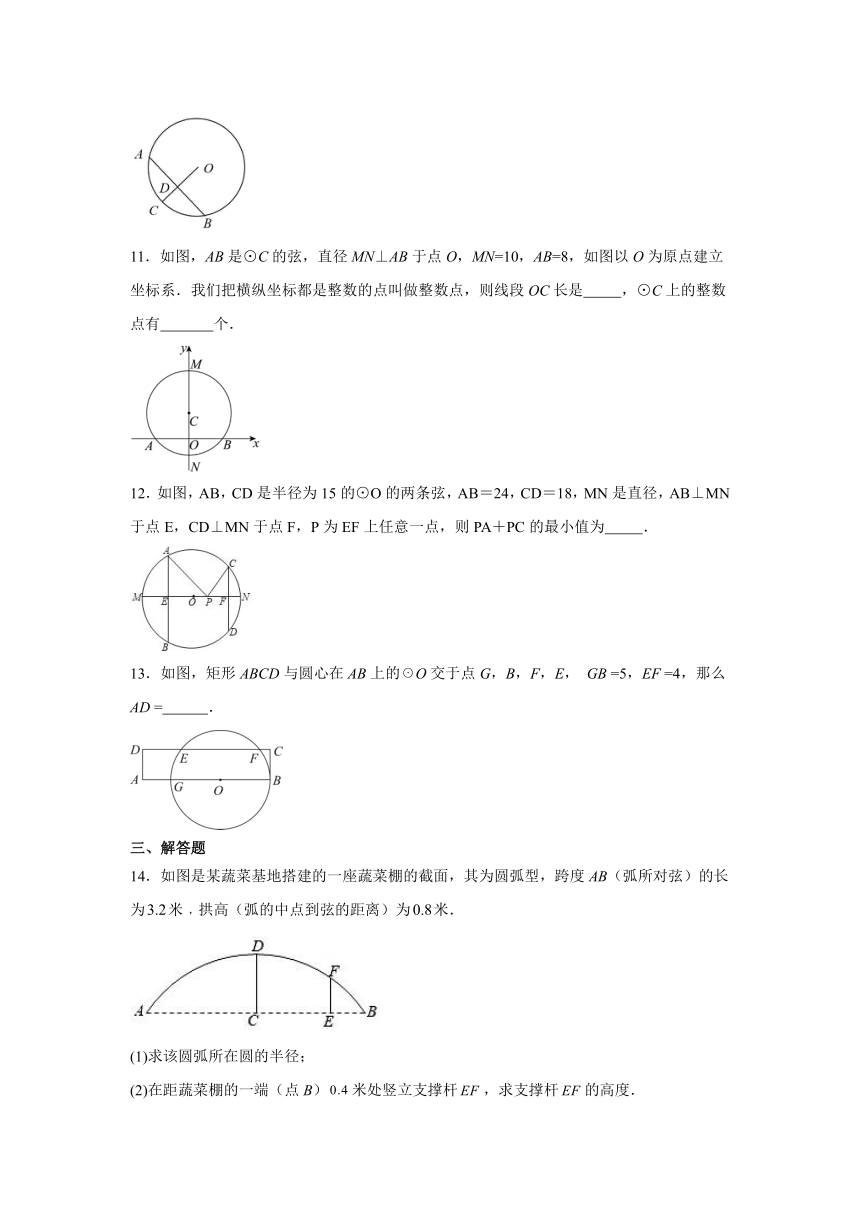
11.如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是 ,⊙C上的整数点有 个.
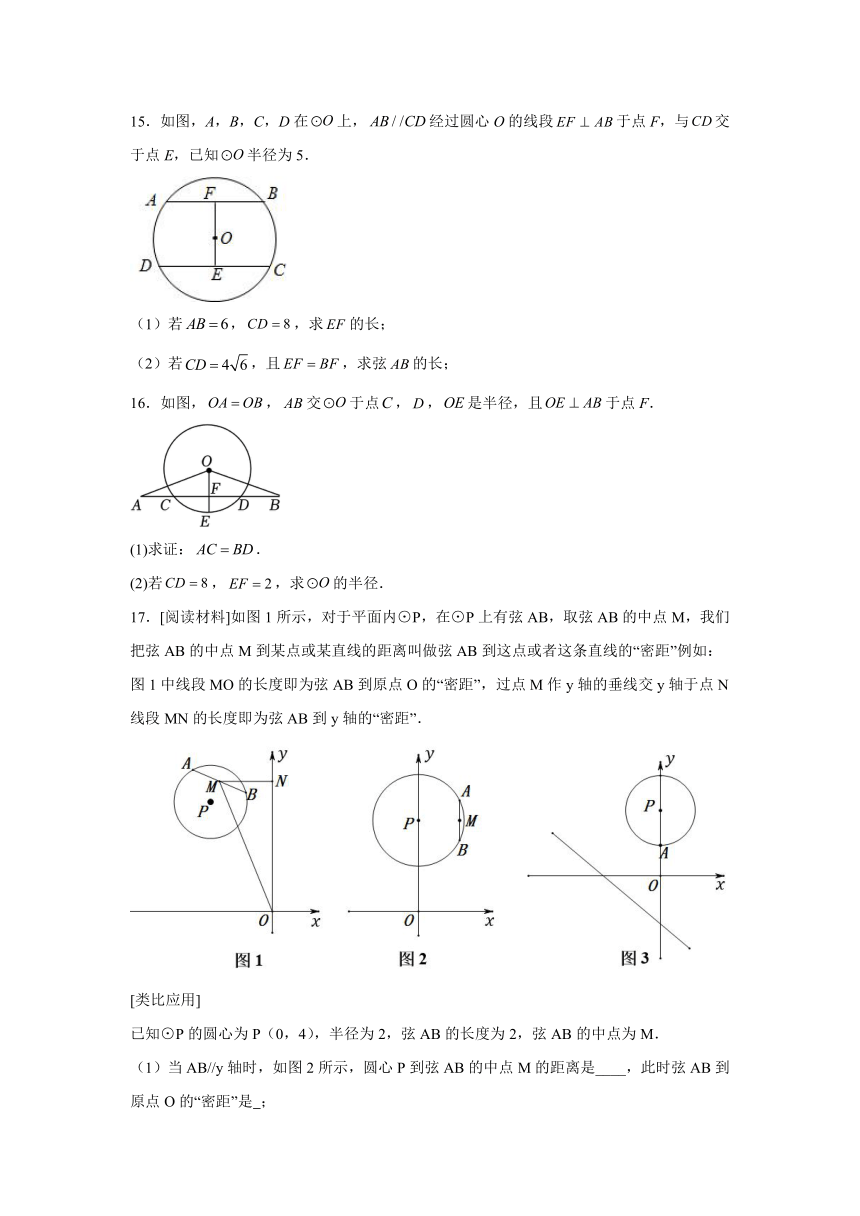
12.如图,AB,CD是半径为15的⊙O的两条弦,AB=24,CD=18,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上任意一点,则PA+PC的最小值为 .
13.如图,矩形ABCD与圆心在AB上的☉O交于点G,B,F,E, GB =5,EF =4,那么AD = .
三、解答题
14.如图是某蔬菜基地搭建的一座蔬菜棚的截面,其为圆弧型,跨度AB(弧所对弦)的长为米﹐拱高(弧的中点到弦的距离)为米.
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端(点B)米处竖立支撑杆,求支撑杆的高度.
15.如图,A,B,C,D在上,经过圆心O的线段于点F,与交于点E,已知半径为5.
(1)若,,求的长;
(2)若,且,求弦的长;
16.如图,,交于点,,是半径,且于点F.
(1)求证:.
(2)若,,求的半径.
17.[阅读材料]如图1所示,对于平面内⊙P,在⊙P上有弦AB,取弦AB的中点M,我们把弦AB的中点M到某点或某直线的距离叫做弦AB到这点或者这条直线的“密距”例如:图1中线段MO的长度即为弦AB到原点O的“密距”,过点M作y轴的垂线交y轴于点N线段MN的长度即为弦AB到y轴的“密距”.
[类比应用]
已知⊙P的圆心为P(0,4),半径为2,弦AB的长度为2,弦AB的中点为M.
(1)当AB//y轴时,如图2所示,圆心P到弦AB的中点M的距离是____,此时弦AB到原点O的“密距”是 ;
(2)①如果弦AB在⊙P上运动,在运动过程中,圆心P到弦AB的中点M的距离变化吗 若不变化,请求出PM的长,若变化,请说明理由.
②直接写出弦AB到原点O的“密距”d的取值范围 ;
[拓展应用]如图3所示,已知⊙P的圆心为P(0,4),半径为2,点A(0,2),点B为⊙P上白一动点,有直线y=-x-3,弦AB到直线y=-x-3的“密距”的最大值是 .(直接写出答案)
参考答案
1--8ACCCC CDC
9.2
10.8.
11.3 12
12.
13.
14.(1)解:设所在的圆心为,为的中点,于,延长至点,
则(米),
设的半径为,
在中,,
∴,
解得,
即该圆弧所在圆的半径为米;
(2)过作于,
则(米),米,
在中, (米),
∵(米),
∴(米),
即支撑杆EF的高度为米.
15.解:(1)连接AO和DO,
∵,且EF过圆心,
∴,
∵,
∴,
∵,
∴,
同理,
,
∴;
(2)如图,连接BO和DO,
∵,
∴,
∴,
设,则,
在中,,
,解得,(舍去),
∴,
∴.
16.(1)证明:,
,
,
,
,
;
(2)解:连接,
设的半径是,
,
,
,
的半径是5.
17.[类比应用](1)如下图2
连接PA、PM、OM、
∵P为圆心,M是弦AB(非直径)的中点
∴PM⊥AB
在RT△PAM中,由勾股定理得
即圆心P到弦AB的中点M的距离是;
∵AB∥y轴
∴PM⊥y轴
在RT△OMP中,由勾股定理得
∴由“密距”的意义得
弦AB到原点O的“密距”是.
(2)①不变化
连接PM、PA、
∵点M是弦AB(非直径)的中点,P为圆心,
∴PM⊥AB,MA=MB=1,
∴PM=
②由图知
∴;
[拓展应用]:如下图3
C是PA中点,连接CM、过C作CD⊥EF于D
∵M是AB(非直径)中点,P是⊙P的圆心
∴PM⊥AB
又∵C是PA中点
∴
当AB是⊙P的直径时,CM=CP=1
∴当B点在⊙P上运动是,M的运动轨迹是以C为圆心,以1为半径的圆.
易知直线y=-x-3与两坐标轴的交点为E(0,-3)、F(-3,0)
∴OE=OF=3,
∴EC=AO+OE+AC=2+3+1=6
又∵x轴⊥y轴
∴∠DEC=45°
∴
由图易知M到EF的最远距离为CD+CM=
所以弦AB到直线y=-x-3的“密距”的最大值为.
一、单选题
1.如图是小明完成的.作法是:取的直径,在上任取一点引弦当点在半圆上移动时点不与A、B重合,的平分线与的交点必( )
A.平分弧 B.三等分弧
C.到点和直径的距离相等 D.到点和点的距离相等
2.如图,的直径,是的弦,,垂足为M,,则的长为( )
A.8 B.12 C.16 D.
3.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则的半径为( )
A.13cm B.16cm C.26cm D.20cm
4.已知△ABC的边BC= ,且△ABC内接于半径为2的⊙O,则∠A的度数是( )
A.60° B.120° C.60°或120° D.90°
5.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
A.1 B.1.5 C.2 D.2.5
6.已知AB、CD是⊙O的两条弦,AB∥CD,AB=6,CD=8,⊙O的半径为5,则AB与CD的距离是( )
A.1 B.7 C.1或7 D.无法确定
7.如图,在半圆中,直径,是半圆上一点,将弧沿弦折叠交于,点是弧的中点.连接,则的最小值为( )
A. B. C. D.
8.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3)
C.点(5,1) D.点(6,1)
二、填空题
9.如图,在半径为5的中,半径与弦垂直,垂足为点D,且,则的长等于 .
10.如图,在中,点是的中点,连接交弦于点,若,,则的长是 .
11.如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是 ,⊙C上的整数点有 个.
12.如图,AB,CD是半径为15的⊙O的两条弦,AB=24,CD=18,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上任意一点,则PA+PC的最小值为 .
13.如图,矩形ABCD与圆心在AB上的☉O交于点G,B,F,E, GB =5,EF =4,那么AD = .
三、解答题
14.如图是某蔬菜基地搭建的一座蔬菜棚的截面,其为圆弧型,跨度AB(弧所对弦)的长为米﹐拱高(弧的中点到弦的距离)为米.
(1)求该圆弧所在圆的半径;
(2)在距蔬菜棚的一端(点B)米处竖立支撑杆,求支撑杆的高度.
15.如图,A,B,C,D在上,经过圆心O的线段于点F,与交于点E,已知半径为5.
(1)若,,求的长;
(2)若,且,求弦的长;
16.如图,,交于点,,是半径,且于点F.
(1)求证:.
(2)若,,求的半径.
17.[阅读材料]如图1所示,对于平面内⊙P,在⊙P上有弦AB,取弦AB的中点M,我们把弦AB的中点M到某点或某直线的距离叫做弦AB到这点或者这条直线的“密距”例如:图1中线段MO的长度即为弦AB到原点O的“密距”,过点M作y轴的垂线交y轴于点N线段MN的长度即为弦AB到y轴的“密距”.
[类比应用]
已知⊙P的圆心为P(0,4),半径为2,弦AB的长度为2,弦AB的中点为M.
(1)当AB//y轴时,如图2所示,圆心P到弦AB的中点M的距离是____,此时弦AB到原点O的“密距”是 ;
(2)①如果弦AB在⊙P上运动,在运动过程中,圆心P到弦AB的中点M的距离变化吗 若不变化,请求出PM的长,若变化,请说明理由.
②直接写出弦AB到原点O的“密距”d的取值范围 ;
[拓展应用]如图3所示,已知⊙P的圆心为P(0,4),半径为2,点A(0,2),点B为⊙P上白一动点,有直线y=-x-3,弦AB到直线y=-x-3的“密距”的最大值是 .(直接写出答案)
参考答案
1--8ACCCC CDC
9.2
10.8.
11.3 12
12.
13.
14.(1)解:设所在的圆心为,为的中点,于,延长至点,
则(米),
设的半径为,
在中,,
∴,
解得,
即该圆弧所在圆的半径为米;
(2)过作于,
则(米),米,
在中, (米),
∵(米),
∴(米),
即支撑杆EF的高度为米.
15.解:(1)连接AO和DO,
∵,且EF过圆心,
∴,
∵,
∴,
∵,
∴,
同理,
,
∴;
(2)如图,连接BO和DO,
∵,
∴,
∴,
设,则,
在中,,
,解得,(舍去),
∴,
∴.
16.(1)证明:,
,
,
,
,
;
(2)解:连接,
设的半径是,
,
,
,
的半径是5.
17.[类比应用](1)如下图2
连接PA、PM、OM、
∵P为圆心,M是弦AB(非直径)的中点
∴PM⊥AB
在RT△PAM中,由勾股定理得
即圆心P到弦AB的中点M的距离是;
∵AB∥y轴
∴PM⊥y轴
在RT△OMP中,由勾股定理得
∴由“密距”的意义得
弦AB到原点O的“密距”是.
(2)①不变化
连接PM、PA、
∵点M是弦AB(非直径)的中点,P为圆心,
∴PM⊥AB,MA=MB=1,
∴PM=
②由图知
∴;
[拓展应用]:如下图3
C是PA中点,连接CM、过C作CD⊥EF于D
∵M是AB(非直径)中点,P是⊙P的圆心
∴PM⊥AB
又∵C是PA中点
∴
当AB是⊙P的直径时,CM=CP=1
∴当B点在⊙P上运动是,M的运动轨迹是以C为圆心,以1为半径的圆.
易知直线y=-x-3与两坐标轴的交点为E(0,-3)、F(-3,0)
∴OE=OF=3,
∴EC=AO+OE+AC=2+3+1=6
又∵x轴⊥y轴
∴∠DEC=45°
∴
由图易知M到EF的最远距离为CD+CM=
所以弦AB到直线y=-x-3的“密距”的最大值为.
同课章节目录
