2022-2023学年西藏拉萨市高二(下)期末数学试卷(文科)(含解析)
文档属性
| 名称 | 2022-2023学年西藏拉萨市高二(下)期末数学试卷(文科)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 295.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 17:13:30 | ||
图片预览



文档简介
2022-2023学年西藏拉萨市高二(下)期末数学试卷(文科)
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知集合,,则( )
A. B. C. D.
2. 复数的虚部是( )
A. B. C. D.
3. 对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A. B.
C. D.
4. 若,则( )
A. B. C. D.
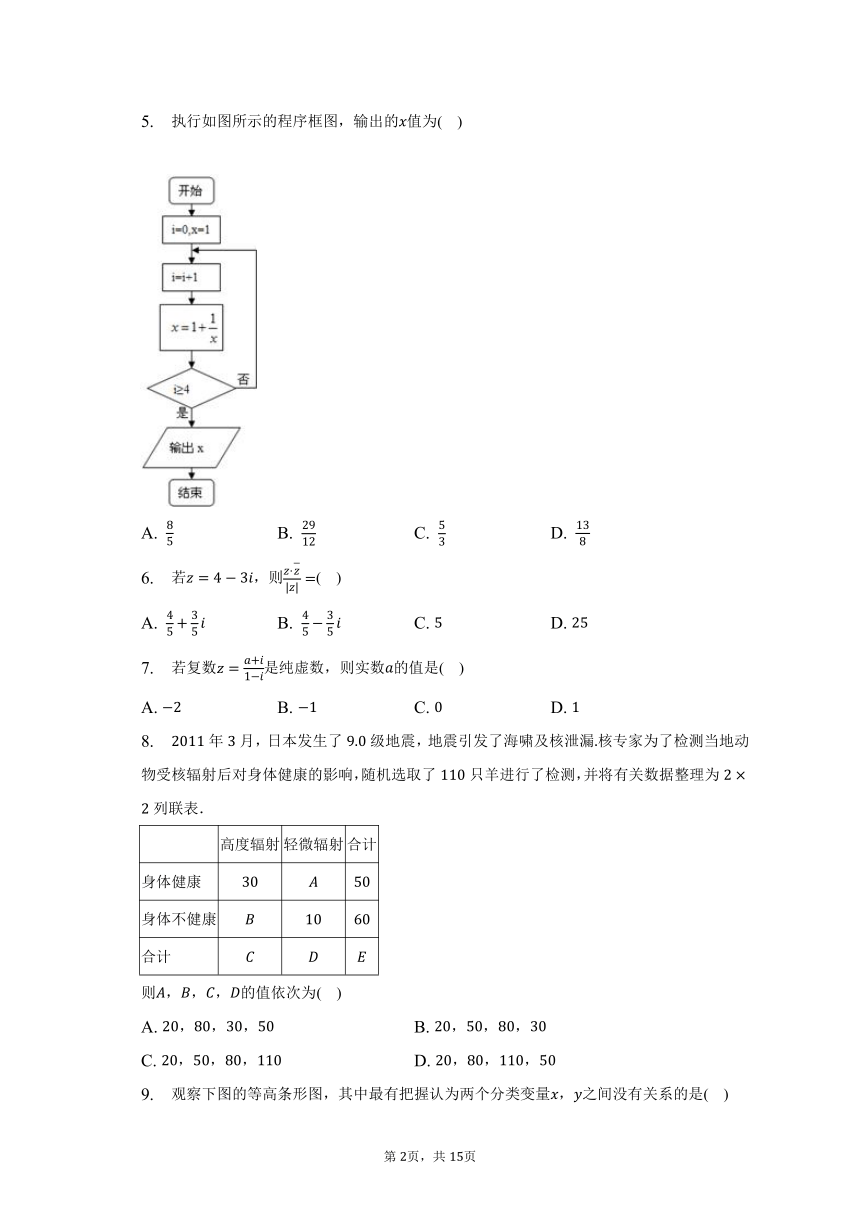
5. 执行如图所示的程序框图,输出的值为( )
A. B. C. D.
6. 若,则( )
A. B. C. D.
7. 若复数是纯虚数,则实数的值是( )
A. B. C. D.
8. 年月,日本发生了级地震,地震引发了海啸及核泄漏核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了只羊进行了检测,并将有关数据整理为列联表.
高度辐射 轻微辐射 合计
身体健康
身体不健康
合计
则,,,的值依次为( )
A. ,,, B. ,,,
C. ,,, D. ,,,
9. 观察下图的等高条形图,其中最有把握认为两个分类变量,之间没有关系的是( )
A. B.
C. D.
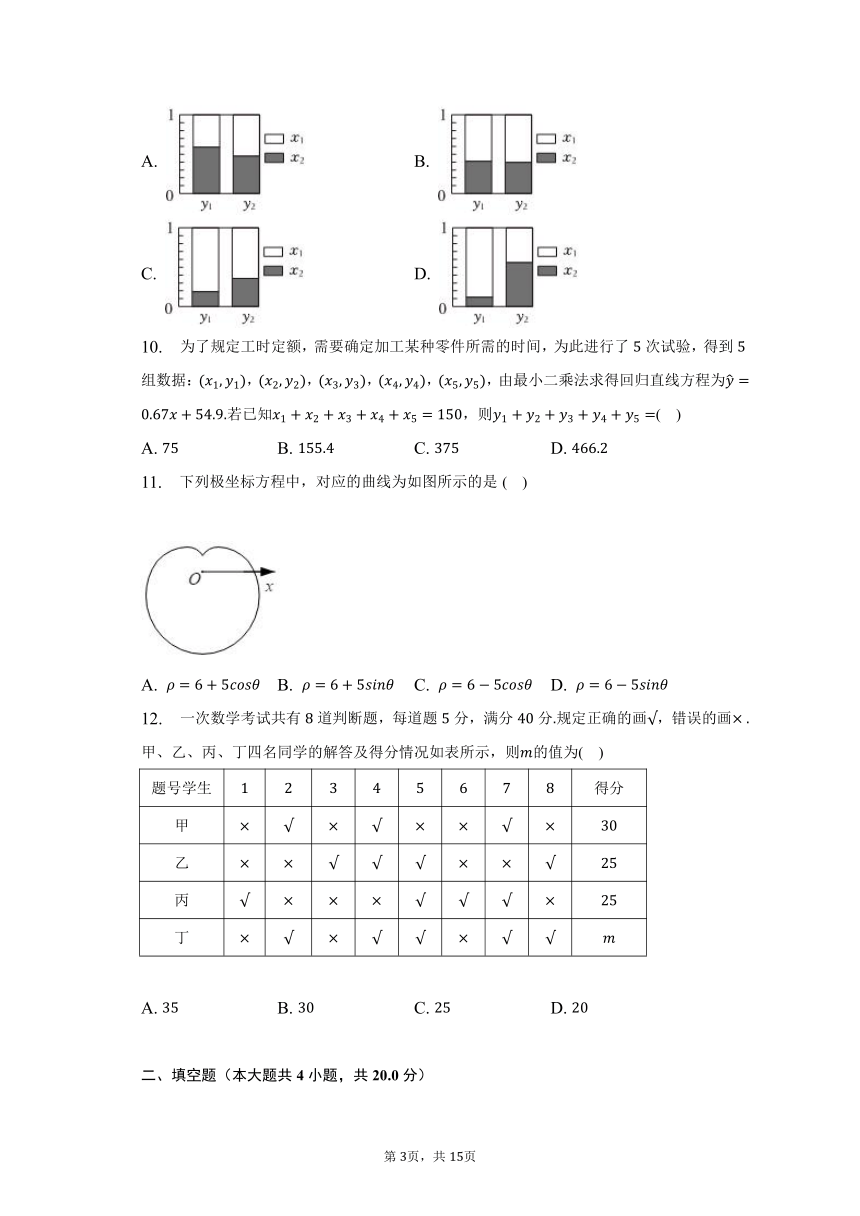
10. 为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了次试验,得到组数据:,,,,,由最小二乘法求得回归直线方程为若已知,则( )
A. B. C. D.
11. 下列极坐标方程中,对应的曲线为如图所示的是( )
A. B. C. D.
12. 一次数学考试共有道判断题,每道题分,满分分规定正确的画,错误的画甲、乙、丙、丁四名同学的解答及得分情况如表所示,则的值为( )
题号学生 得分
甲
乙
丙
丁
A. B. C. D.
二、填空题(本大题共4小题,共20.0分)
13. 某市政府调查市民收入增减与旅游需求的关系时,采用独立性检验法抽查了人,计算发现,根据这一数据,市政府断言市民收入增减与旅游需求有关的可信度是______
附:常用小概率值和临界值表:
14. ______ .
15. 在极坐标系中,点,,则线段的长为______ .
16. 已知复数,若在复平面内对应的点位于第四象限,写出一个满足条件的 ______ .
三、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知复数是虚数单位.
求复数的共轭复数;
若,求,的值.
18. 本小题分
某大学艺术专业名学生参加某次测评,根据男、女学生人数比例使用分层随机抽样的方法从中随机抽取了名学生,记录他们的分数,将数据分成组:,,,,并整理得到如图的频率分布直方图.
估计总体名学生中分数小于的人数;
已知样本中分数小于的学生有人,试估计总体中分数在区间内的人数.
19. 本小题分
在平面直角坐标系中,曲线的参数方程为其中为参数以坐标原点为极点,轴非负半轴为极轴建立极坐标系,直线的极坐标方程为.
求直线的直角坐标方程和曲线的普通方程;
设直线与曲线交于,两点,求线段的长度.
20. 本小题分
垃圾是人类日常生活和生产中产生的废弃物,由于排出量大,成分复杂多样,且具有污染性,所以需要无害化、减量化处理某省为调查产生的垃圾数量,采用简单随机抽样的方法抽取个县城进行了分析,得到样本数据,其中和分别表示第个县城的人口单位:万人和该县年垃圾产生总量单位:吨,并计算得:,,,,.
求这个县年垃圾产生总量的平均值;
请用相关系数说明该组数据中与之间的关系可用线性回归模型进行拟合当时,与的相关关系较强,否则相关关系较弱
参考公式:相关系数.
21. 本小题分
随着互联网的发展,网络已成为人们日常学习、工作和生活不可或缺的部分,互联网在带给人们生活便捷与高效工作的同时,网络犯罪也日益增多为了防范网络犯罪与网络诈骗,某学校举办“网络安全宣传倡议”活动该学校从全体学生中随机抽取了名男生和名女生对“网络安全宣传倡议”的了解情况进行问卷调查下面是问卷调查得分的频率分布表:
成绩分
频率
将得分不低于分的学生视作了解,已知有名男生问卷调查得分不低于分.
根据已知条件完成下面列联表;
男 女 合计
了解
不了解
合计
判断是否有的把握认为对“网络安全宣传倡议”的了解情况与性别有关?
参考公式:,其中.
参考数据:
22. 本小题分
如图所示形如花瓣的曲线称为四叶玫瑰线,在极坐标系中,其极坐标方程为.
若射线与相交于异于极点的点,求;
若,为上的两点,且,求面积的最大值.
答案和解析
1.【答案】
【解析】
【分析】
根据集合的交集运算,可直接求得答案.
本题考查集合的运算,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.
【解答】
解:由于集合,,
故A,
故选:.
2.【答案】
【解析】解:因为,
所以复数的虚部为.
故选:.
根据复数代数形式的乘法运算化简复数,再根据复数的概念判断即可.
本题主要考查复数的四则运算,以及虚部的定义,属于基础题.
3.【答案】
【解析】
【分析】
本题考查两个变量的线性相关,考查相关系数,属于基础题.
根据题目给出的散点图,先判断是正相关还是负相关,然后根据点的集中程度分析相关系数的大小.
【解答】
解:由给出的四组数据的散点图可以看出,
图和图是正相关,相关系数大于,
图和图是负相关,相关系数小于,
图和图的点相对更加集中,所以相关性要强,所以接近于,接近于,
由此可得.
故选:.
4.【答案】
【解析】
【分析】
本题主要考查复数代数形式的乘法和除法法则,属于基础题.
利用复数的运算法则求解即可.
【解答】
解:由,得
.
故选D.
5.【答案】
【解析】解:由程序框图知:程序第一次运行,;
第二次运行,;
第三次运行,;
第四次运行,.
满足条件,输出.
故选:.
根据框图的流程依次计算程序运行的结果,直到满足条件,计算输出的值.
本题考查了循环结构的程序框图,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法.
6.【答案】
【解析】解:,
所以,,
所以,
所以.
故选:.
根据复数代数形式的乘法运算及模的计算公式计算可得.
本题主要考查共轭复数的定义,复数的四则运算,属于基础题.
7.【答案】
【解析】解:是纯虚数,
,解得:.
故选:.
利用复数代数形式的乘除运算化简,由实部为且虚部不为求得答案.
本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.
8.【答案】
【解析】解:,
,
,
,
,.
故选:.
根据 列联表分别计算,,,即可.
本题主要考查独立性检验的应用,属于基础题.
9.【答案】
【解析】解:根据题意,在等高的条形图中,当,所占比例相差越大时,越有把握认为两个分类变量,之间有关系,
分析选项可得:选项中,,所占比例最接近,
所以选项最有把握认为两个分类变量,之间没有关系.
故选:.
根据题意,由等高条形图的意义分析可得答案.
本题考查等高条形图的应用,涉及分类变量关系强弱的判断,属于基础题.
10.【答案】
【解析】解:,回归直线方程为.
可得:.
则.
故选:.
由题意求出代入公式求值,从而得到,即可求的值.
本题考查了线性回归方程的求法及应用,属于基础题.
11.【答案】
【解析】
【分析】
本题考查了极坐标方程、数形结合方法、三角函数的单调性,考查了推理能力与计算能力,属于中档题.
由图形可知:时,取得最大值,即可判断出结论.
【解答】
解:由图形可知:时,取得最大值,
只有满足上述条件.
故选D.
12.【答案】
【解析】解:因为乙丙的第,题答案相同,且总得分都是分,所以第,两题答案正确;
又因为甲得分分,即甲错两题且第,题与乙,丙不同,所以其余题答案均正确,故这道判断题的答案分别是;
对比丁的答案,可知其第,两题错误,故得分,
故选:.
由乙丙的答案和得分得出第,两题答案正确;由甲的得分结合乙丙的答案可得其余题答案均正确;由正确答案求出丁的得分,可得值.
本题考查合情推理,考查学生阅读能力和逻辑思维能力,属于基础题.
13.【答案】
【解析】解:由已知可得,
所以市政府断言市民收入增减与旅游需求有关的可信度是.
故答案为:.
由的观测值结合临界值表得出结论.
本题主要考查了独立性检验的应用,属于基础题.
14.【答案】
【解析】解:,
.
故答案为:.
根据复数的运算性质即可得到结论.
本题主要考查复数的基本运算,利用是解决本题的关键,比较基础.
15.【答案】
【解析】解:由已知,,
线段的长为.
故答案为:.
根据极坐标系中两点间的距离公式,求出线段的长即可.
本题主要考查极坐标刻画点的位置,属于基础题.
16.【答案】答案不唯一
【解析】解:当时,
,其在复平面内对应的点位于第四象限.
故答案为:答案不唯一.
根据已知条件,结合复数的几何意义,以及复数的四则运算,即可求解.
本题主要考查复数的几何意义,以及复数的四则运算,属于基础题.
17.【答案】解:,
则.
因为,
将代入上式,即,化简整理可得,,
所以,解得.
【解析】根据已知条件,先对化简,再结合共轭复数的定义,即可求解.
根据已知条件,结合复数相等的条件,以及复数的四则运算,即可求解.
本题主要考查复数的四则运算,以及共轭复数的定义,属于基础题.
18.【答案】解:根据频率分布直方图可知,样本中分数不小于的频率为,
所以样本中分数小于的频率为,
所以估计总体名学生中分数小于的人数为;
根据题意,样本中分数不小于的频率为,
样本中分数在区间内的人数为,
所以总体中分数在区间内的人数估计为.
【解析】根据频率分布直方图求出样本中分数小于的频率,进而求出总体名学生中分数小于的人数;
先求出样本中分数在区间内的人数,用样本估计总体,进而求出总体中分数在区间内的人数.
本题主要考查频率分布直方图的应用,属于基础题.
19.【答案】解:由题意:,所以曲线是圆心为,半径的圆;
直线:,
由,,得直线的直角坐标方程为:;
由的结论作下图:
到直线的距离,;
综上,曲线的普通方程为:,直线的直角坐标方程为:,.
【解析】消参,将参数方程转化为普通方程,根据直角坐标与极坐标的关系将直线转化为直角坐标方程;
作图,根据几何关系求解.
本题主要考查简单曲线的极坐标方程,考查转化能力,属于中档题.
20.【答案】解:依题意这个县年垃圾产生总量的平均值为吨.
依题意,
因为与的相关系数接近,所以与之间具有较强的线性相关关系,可用线性回归模型进行拟合.
【解析】根据直接计算可得;
根据所给数据计算出相关系数,即可说明.
本题主要考查相关系数的公式,属于基础题.
21.【答案】解:问卷调查结果为“了解”的学生人数为,
又因为其中男生有人,所以其中女生有人,
所以列联表如下:
男 女 合计
了解
不了解
合计
零假设:对“网络安全宣传倡议”的了解情况与性别无关,
由可得,
根据小概率的独立性检验,我们推断不成立,
即认为对“网络安全宣传倡议”的了解情况与性别有关,此推断犯错误的概率不大于,
即有的把握认为对“网络安全宣传倡议”的了解情况与性别有关.
【解析】根据频率分布表求出问卷调查结果为“了解”的学生人数,从而求出其中女生的人数,即可得到列联表;
计算出卡方,即可判断.
本题主要考查独立性检验公式,属于基础题.
22.【答案】解:在极坐标系中,曲线的极坐标方程为,
若射线与极坐标方程相交于点,
所以,
故.
设,,且,
故,
当,,整理得,,
故面积的最大值为.
【解析】直接利用曲线与直线的位置关系求出极径的长;
利用三角形的面积公式和三角函数的关系式的变换及正弦型函数的性质求出三角形面积的最大值.
本题考查的知识要点:极坐标方程的应用,三角形的面积公式,三角函数的关系式的变换,正弦型函数的性质,主要考查学生的理解能力和计算能力,属于中档题.
第1页,共1页
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知集合,,则( )
A. B. C. D.
2. 复数的虚部是( )
A. B. C. D.
3. 对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A. B.
C. D.
4. 若,则( )
A. B. C. D.
5. 执行如图所示的程序框图,输出的值为( )
A. B. C. D.
6. 若,则( )
A. B. C. D.
7. 若复数是纯虚数,则实数的值是( )
A. B. C. D.
8. 年月,日本发生了级地震,地震引发了海啸及核泄漏核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了只羊进行了检测,并将有关数据整理为列联表.
高度辐射 轻微辐射 合计
身体健康
身体不健康
合计
则,,,的值依次为( )
A. ,,, B. ,,,
C. ,,, D. ,,,
9. 观察下图的等高条形图,其中最有把握认为两个分类变量,之间没有关系的是( )
A. B.
C. D.
10. 为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了次试验,得到组数据:,,,,,由最小二乘法求得回归直线方程为若已知,则( )
A. B. C. D.
11. 下列极坐标方程中,对应的曲线为如图所示的是( )
A. B. C. D.
12. 一次数学考试共有道判断题,每道题分,满分分规定正确的画,错误的画甲、乙、丙、丁四名同学的解答及得分情况如表所示,则的值为( )
题号学生 得分
甲
乙
丙
丁
A. B. C. D.
二、填空题(本大题共4小题,共20.0分)
13. 某市政府调查市民收入增减与旅游需求的关系时,采用独立性检验法抽查了人,计算发现,根据这一数据,市政府断言市民收入增减与旅游需求有关的可信度是______
附:常用小概率值和临界值表:
14. ______ .
15. 在极坐标系中,点,,则线段的长为______ .
16. 已知复数,若在复平面内对应的点位于第四象限,写出一个满足条件的 ______ .
三、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知复数是虚数单位.
求复数的共轭复数;
若,求,的值.
18. 本小题分
某大学艺术专业名学生参加某次测评,根据男、女学生人数比例使用分层随机抽样的方法从中随机抽取了名学生,记录他们的分数,将数据分成组:,,,,并整理得到如图的频率分布直方图.
估计总体名学生中分数小于的人数;
已知样本中分数小于的学生有人,试估计总体中分数在区间内的人数.
19. 本小题分
在平面直角坐标系中,曲线的参数方程为其中为参数以坐标原点为极点,轴非负半轴为极轴建立极坐标系,直线的极坐标方程为.
求直线的直角坐标方程和曲线的普通方程;
设直线与曲线交于,两点,求线段的长度.
20. 本小题分
垃圾是人类日常生活和生产中产生的废弃物,由于排出量大,成分复杂多样,且具有污染性,所以需要无害化、减量化处理某省为调查产生的垃圾数量,采用简单随机抽样的方法抽取个县城进行了分析,得到样本数据,其中和分别表示第个县城的人口单位:万人和该县年垃圾产生总量单位:吨,并计算得:,,,,.
求这个县年垃圾产生总量的平均值;
请用相关系数说明该组数据中与之间的关系可用线性回归模型进行拟合当时,与的相关关系较强,否则相关关系较弱
参考公式:相关系数.
21. 本小题分
随着互联网的发展,网络已成为人们日常学习、工作和生活不可或缺的部分,互联网在带给人们生活便捷与高效工作的同时,网络犯罪也日益增多为了防范网络犯罪与网络诈骗,某学校举办“网络安全宣传倡议”活动该学校从全体学生中随机抽取了名男生和名女生对“网络安全宣传倡议”的了解情况进行问卷调查下面是问卷调查得分的频率分布表:
成绩分
频率
将得分不低于分的学生视作了解,已知有名男生问卷调查得分不低于分.
根据已知条件完成下面列联表;
男 女 合计
了解
不了解
合计
判断是否有的把握认为对“网络安全宣传倡议”的了解情况与性别有关?
参考公式:,其中.
参考数据:
22. 本小题分
如图所示形如花瓣的曲线称为四叶玫瑰线,在极坐标系中,其极坐标方程为.
若射线与相交于异于极点的点,求;
若,为上的两点,且,求面积的最大值.
答案和解析
1.【答案】
【解析】
【分析】
根据集合的交集运算,可直接求得答案.
本题考查集合的运算,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.
【解答】
解:由于集合,,
故A,
故选:.
2.【答案】
【解析】解:因为,
所以复数的虚部为.
故选:.
根据复数代数形式的乘法运算化简复数,再根据复数的概念判断即可.
本题主要考查复数的四则运算,以及虚部的定义,属于基础题.
3.【答案】
【解析】
【分析】
本题考查两个变量的线性相关,考查相关系数,属于基础题.
根据题目给出的散点图,先判断是正相关还是负相关,然后根据点的集中程度分析相关系数的大小.
【解答】
解:由给出的四组数据的散点图可以看出,
图和图是正相关,相关系数大于,
图和图是负相关,相关系数小于,
图和图的点相对更加集中,所以相关性要强,所以接近于,接近于,
由此可得.
故选:.
4.【答案】
【解析】
【分析】
本题主要考查复数代数形式的乘法和除法法则,属于基础题.
利用复数的运算法则求解即可.
【解答】
解:由,得
.
故选D.
5.【答案】
【解析】解:由程序框图知:程序第一次运行,;
第二次运行,;
第三次运行,;
第四次运行,.
满足条件,输出.
故选:.
根据框图的流程依次计算程序运行的结果,直到满足条件,计算输出的值.
本题考查了循环结构的程序框图,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法.
6.【答案】
【解析】解:,
所以,,
所以,
所以.
故选:.
根据复数代数形式的乘法运算及模的计算公式计算可得.
本题主要考查共轭复数的定义,复数的四则运算,属于基础题.
7.【答案】
【解析】解:是纯虚数,
,解得:.
故选:.
利用复数代数形式的乘除运算化简,由实部为且虚部不为求得答案.
本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.
8.【答案】
【解析】解:,
,
,
,
,.
故选:.
根据 列联表分别计算,,,即可.
本题主要考查独立性检验的应用,属于基础题.
9.【答案】
【解析】解:根据题意,在等高的条形图中,当,所占比例相差越大时,越有把握认为两个分类变量,之间有关系,
分析选项可得:选项中,,所占比例最接近,
所以选项最有把握认为两个分类变量,之间没有关系.
故选:.
根据题意,由等高条形图的意义分析可得答案.
本题考查等高条形图的应用,涉及分类变量关系强弱的判断,属于基础题.
10.【答案】
【解析】解:,回归直线方程为.
可得:.
则.
故选:.
由题意求出代入公式求值,从而得到,即可求的值.
本题考查了线性回归方程的求法及应用,属于基础题.
11.【答案】
【解析】
【分析】
本题考查了极坐标方程、数形结合方法、三角函数的单调性,考查了推理能力与计算能力,属于中档题.
由图形可知:时,取得最大值,即可判断出结论.
【解答】
解:由图形可知:时,取得最大值,
只有满足上述条件.
故选D.
12.【答案】
【解析】解:因为乙丙的第,题答案相同,且总得分都是分,所以第,两题答案正确;
又因为甲得分分,即甲错两题且第,题与乙,丙不同,所以其余题答案均正确,故这道判断题的答案分别是;
对比丁的答案,可知其第,两题错误,故得分,
故选:.
由乙丙的答案和得分得出第,两题答案正确;由甲的得分结合乙丙的答案可得其余题答案均正确;由正确答案求出丁的得分,可得值.
本题考查合情推理,考查学生阅读能力和逻辑思维能力,属于基础题.
13.【答案】
【解析】解:由已知可得,
所以市政府断言市民收入增减与旅游需求有关的可信度是.
故答案为:.
由的观测值结合临界值表得出结论.
本题主要考查了独立性检验的应用,属于基础题.
14.【答案】
【解析】解:,
.
故答案为:.
根据复数的运算性质即可得到结论.
本题主要考查复数的基本运算,利用是解决本题的关键,比较基础.
15.【答案】
【解析】解:由已知,,
线段的长为.
故答案为:.
根据极坐标系中两点间的距离公式,求出线段的长即可.
本题主要考查极坐标刻画点的位置,属于基础题.
16.【答案】答案不唯一
【解析】解:当时,
,其在复平面内对应的点位于第四象限.
故答案为:答案不唯一.
根据已知条件,结合复数的几何意义,以及复数的四则运算,即可求解.
本题主要考查复数的几何意义,以及复数的四则运算,属于基础题.
17.【答案】解:,
则.
因为,
将代入上式,即,化简整理可得,,
所以,解得.
【解析】根据已知条件,先对化简,再结合共轭复数的定义,即可求解.
根据已知条件,结合复数相等的条件,以及复数的四则运算,即可求解.
本题主要考查复数的四则运算,以及共轭复数的定义,属于基础题.
18.【答案】解:根据频率分布直方图可知,样本中分数不小于的频率为,
所以样本中分数小于的频率为,
所以估计总体名学生中分数小于的人数为;
根据题意,样本中分数不小于的频率为,
样本中分数在区间内的人数为,
所以总体中分数在区间内的人数估计为.
【解析】根据频率分布直方图求出样本中分数小于的频率,进而求出总体名学生中分数小于的人数;
先求出样本中分数在区间内的人数,用样本估计总体,进而求出总体中分数在区间内的人数.
本题主要考查频率分布直方图的应用,属于基础题.
19.【答案】解:由题意:,所以曲线是圆心为,半径的圆;
直线:,
由,,得直线的直角坐标方程为:;
由的结论作下图:
到直线的距离,;
综上,曲线的普通方程为:,直线的直角坐标方程为:,.
【解析】消参,将参数方程转化为普通方程,根据直角坐标与极坐标的关系将直线转化为直角坐标方程;
作图,根据几何关系求解.
本题主要考查简单曲线的极坐标方程,考查转化能力,属于中档题.
20.【答案】解:依题意这个县年垃圾产生总量的平均值为吨.
依题意,
因为与的相关系数接近,所以与之间具有较强的线性相关关系,可用线性回归模型进行拟合.
【解析】根据直接计算可得;
根据所给数据计算出相关系数,即可说明.
本题主要考查相关系数的公式,属于基础题.
21.【答案】解:问卷调查结果为“了解”的学生人数为,
又因为其中男生有人,所以其中女生有人,
所以列联表如下:
男 女 合计
了解
不了解
合计
零假设:对“网络安全宣传倡议”的了解情况与性别无关,
由可得,
根据小概率的独立性检验,我们推断不成立,
即认为对“网络安全宣传倡议”的了解情况与性别有关,此推断犯错误的概率不大于,
即有的把握认为对“网络安全宣传倡议”的了解情况与性别有关.
【解析】根据频率分布表求出问卷调查结果为“了解”的学生人数,从而求出其中女生的人数,即可得到列联表;
计算出卡方,即可判断.
本题主要考查独立性检验公式,属于基础题.
22.【答案】解:在极坐标系中,曲线的极坐标方程为,
若射线与极坐标方程相交于点,
所以,
故.
设,,且,
故,
当,,整理得,,
故面积的最大值为.
【解析】直接利用曲线与直线的位置关系求出极径的长;
利用三角形的面积公式和三角函数的关系式的变换及正弦型函数的性质求出三角形面积的最大值.
本题考查的知识要点:极坐标方程的应用,三角形的面积公式,三角函数的关系式的变换,正弦型函数的性质,主要考查学生的理解能力和计算能力,属于中档题.
第1页,共1页
同课章节目录
