2022-2023学年湖南省怀化市会同县七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年湖南省怀化市会同县七年级(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 361.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 17:54:01 | ||
图片预览




文档简介
2022-2023学年湖南省怀化市会同县七年级(下)期末数学试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. “潮涌”是年杭州亚运会会徽,钱塘江和钱江潮头是会徽的形象核心,如图是会徽的一部分,在以下四个选项中,能由该图经过平移得到的是( )
A. B.
C. D.
2. 如图,直线、相交于点,若,则的度数是( )
A.
B.
C.
D.
3. 我国古代算法统宗里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果一间客房住人,那么有人无房可住;如果一间客房住人,那么就空出一间客房,若设该店有客房间,房客人,则列出关于,的二元一次方程组正确的是( )
A. B. C. D.
4. 计算的结果是( )
A. B. C. D.
5. 如图,点在直线上,若,则的大小为 ( )
A. B. C. D.
6. 如图,已知,如果,那么的度数为( )
A.
B.
C.
D.
7. 下列因式分解正确的是( )
A. B.
C. D.
8. 某校举行“预防溺水,从我做起”演讲比赛,位评委给选手甲的评分如下:,,,,,,,则这组数据的众数和中位数分别是( )
A. , B. , C. , D. ,
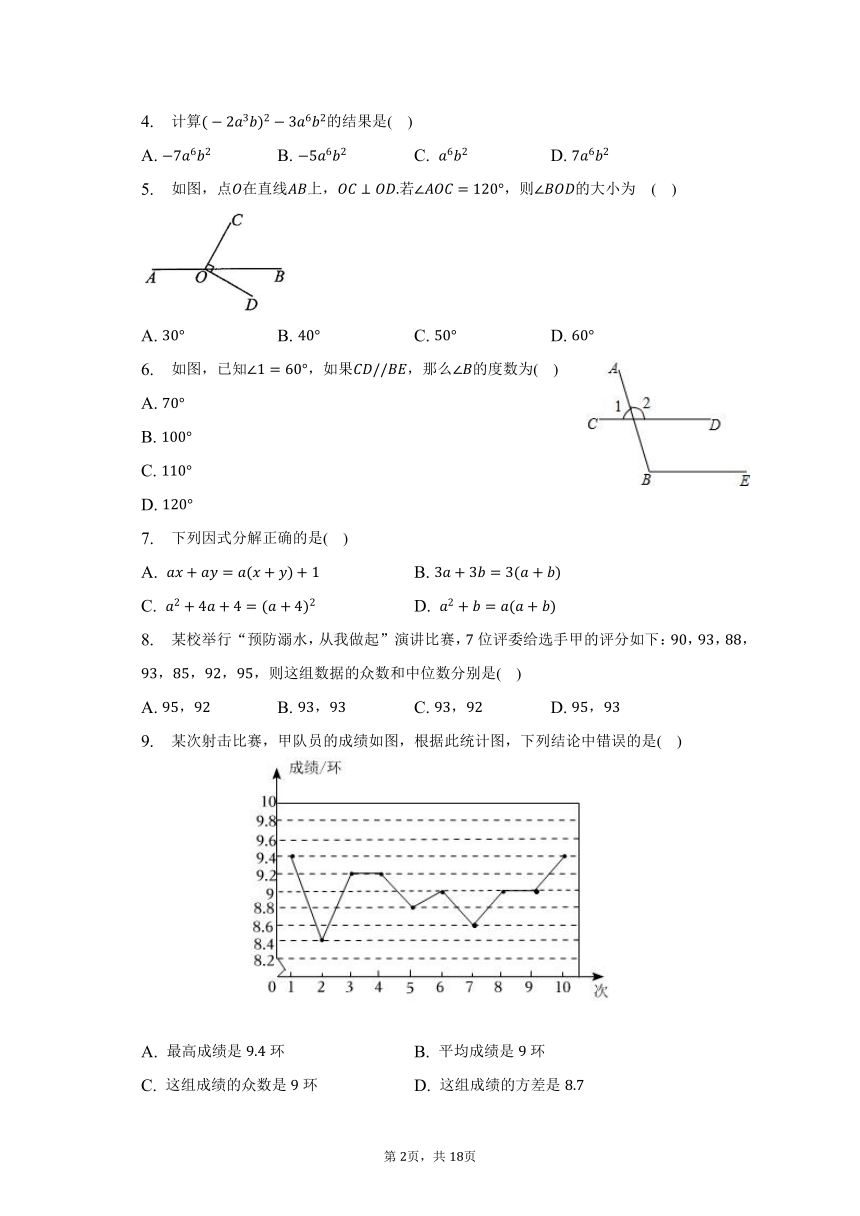
9. 某次射击比赛,甲队员的成绩如图,根据此统计图,下列结论中错误的是( )
A. 最高成绩是环 B. 平均成绩是环
C. 这组成绩的众数是环 D. 这组成绩的方差是
10. 如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从出发爬到,则( )
A. 乙比甲先到
B. 甲比乙先到
C. 甲和乙同时到
D. 无法确定
二、填空题(本大题共6小题,共24.0分)
11. 如图,木棒、与分别在、处用可旋转的螺丝铆住,,,将木棒绕点逆时针旋转到与木棒平行的位置,则至少要旋转______
12. 希望村在落实“脱贫先修路”的计划中需要在家乡河上建一座桥,如图所示的方案中,在______ 处建桥最合适,理由是______ .
13. 甲、乙两名学生次立定跳远成绩的平均数相同,若甲次立定跳远成绩的方差为,乙次立定跳远成绩的方差为,则甲、乙两名学生次立定跳远成绩比较稳定的是______填“甲”或“乙”
14. 如图,将向右平移得到,如果的周长是,那么五边形的周长是______.
15. 如图,射线,,,则的度数是______ .
16. 如图,直线,,,则______.
三、解答题(本大题共8小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知关于、的二元一次方程组,则的值为______.
若,且,求的值.
18. 本小题分
如图,从边长为的大正方形中剪去一个边长为的小正方形,把剩下的阴影部分拼成如图所示的长方形.
上述操作能验证的公式是______ ;
请应用这个公式完成下列各题:
已知,,则 ______ ;
计算:.
19. 本小题分
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,的三个顶点坐标分别为,,.
画出关于轴对称的;
画出绕点逆时针旋转后得到的
20. 本小题分
甲、乙两位同学一起解方程组,甲正确地解得,乙仅因抄错了题中的,而求得.
求原方程组中,,的值.
写出求原方程组解的过程.
21. 本小题分
某同学在,两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是元,且随身听的单价比书包单价的倍少元.
求该同学看中的随身听和书包单价各是多少元?
某一天该同学上街,恰好赶上商家促销,超市所有商品打八五折销售,超市全场购物满元返购物券元销售不足元不返券,购物券全场通用,但他只带了元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
22. 本小题分
幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中把洛书用今天的数学符号翻译出来,就是一个三阶幻方如图,将个数填在三行三列的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方图的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,求的值.
23. 本小题分
“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯射线从开始顺时针旋转至便立即回转,灯射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是每秒度,灯转动的速度是每秒度,假定主道路是平行的,即,且::.
填空:______;
如图,
若灯射线先转动,灯射线才开始转动,在灯射线到达之前,设灯转动秒,则______,______;用含的式子表示
在的条件下,若,则______秒.
如图,若两灯同时转动,在灯射线到达之前.若射出的光束交于点,过作交于点,且,则在转动过程中,请探究与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
24. 本小题分
为了加强心理健康教育,某校组织七年级两班学生进行了心理健康常识测试分数为整数,满分为分,已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
求班学生中测试成绩为分的人数;
请确定下表中,,的值只要求写出求的计算过程;
统计量 平均数 众数 中位数 方差
班
班
从上表中选择合适的统计量,说明哪个班的成绩更均匀.
答案和解析
1.【答案】
【解析】
解:根据图形的平移可知:能由该图经过平移得到的是,
故选:.
【分析】本题考查了图形的平移,解决本题的关键是掌握平移的概念.
根据平移的概念即可进行判断.
2.【答案】
【解析】解:,与是对顶角,
.
故选:.
根据对顶角相等可得.
本题考查了对顶角,解题的关键是熟练掌握对顶角的性质:对顶角相等.
3.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组,根据题意得出方程组是解决问题的关键.
设该店有客房间,房客人,根据“一房七客多七客,一房九客一房空”得出方程组即可.
【解答】
解:设该店有客房间,房客人,
根据题意得:
故选:.
4.【答案】
【解析】解:原式,
故选:.
先根据积的乘方法则计算,再合并同类项.
本题主要考查了积的乘方,合并同类项,关键是熟记法则.
5.【答案】
【解析】解:因为,,
所以,
又因为,
所以,
所以,
故选:.
根据平角的定义求出的度数,再根据垂直的定义求出答案.
本题考查平角及垂直的定义,理解互相垂直的定义是解决问题的关键.
6.【答案】
【解析】解:,
.
,
.
故选D.
先根据补角的定义求出的度数,再由平行线的性质即可得出结论.
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
7.【答案】
【解析】解:选项,,故该选项不符合题意;
选项,,故该选项符合题意;
选项,,故该选项不符合题意;
选项,与没有公因式,故该选项不符合题意;
故选:.
根据因式分解的定义和因式分解常用的两种方法:提公因式法和公式法判断即可.
本题考查了因式分解,掌握是解题的关键.
8.【答案】
【解析】解:将这组数据从小到大排列为:,,,,,,,
这组数据的众数是,中位数是.
故选:.
将这组数据从小到大排列,出现次数最多的数据就是众数,处于中间位置的数就是这组数据的中位数.
本题考查了众数,中位数,掌握将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数是解题的关键.
9.【答案】
【解析】解:由题意可知,最高成绩是环,故选项A不符合题意;
平均成绩是环,故选项B不合题意;
这组成绩的众数是环,故选项C不合题意;
这组成绩的方差是,故选项D符合题意.
故选:.
根据题意分别求出这组数据的平均数、众数和方差即可判断.
此题主要考查了折线统计图,加权平均数,众数和方差,掌握平均数和方差的计算公式是解题关键.
10.【答案】
【解析】
【分析】
本题考查了生活中的平移现象,结合图形找出甲、乙两只蚂蚁的行程相等是解题的关键.
根据平移可得出两蚂蚁行程相同,结合二者速度相同即可得出结论.
【解答】
解:甲、乙两只蚂蚁的行程相同,且两只蚂蚁的速度相同,
两只蚂蚁同时到达.
故选C.
11.【答案】
【解析】解:当时,,
,,
需要变小,即将木棒绕点逆时针旋转.
故答案为:.
由平行线的判定“同位角相等,两直线平行”可知,时,,即需要变小,即将木棒绕点逆时针旋转即可.
本题主要考查平行线的性质与判定,熟知相关定理是解题基础.
12.【答案】 垂线段最短
【解析】解:,
根据垂线段最短,在处建桥最合适,
故答案为:,垂线段最短.
根据垂线段的性质得出答案.
本题考查了垂线段最短的性质,掌握垂线段最短是解题的关键.
13.【答案】乙
【解析】解:,,
,
甲、乙两名学生次立定跳远成绩的平均数相同,
甲、乙两名学生次立定跳远成绩比较稳定的是乙,
故答案为:乙.
根据方差的意义可直接求解.
此题主要考查了方差,关键是掌握方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
14.【答案】
【解析】解:向右平移得到,
,,
的周长是,即,
五边形的周长.
故答案为.
先利用平移的性质得到,,,然后利用等线段代换得到五边形的周长.
本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行或共线且相等.
15.【答案】
【解析】解:过作,
,
,
,,
,
,
,
.
故答案为:.
过作,得到,推出,,求出,得到,因此.
本题考查平行线的性质,关键是过作,得到,由平行线的性质来解决问题.
16.【答案】
【解析】解:如图,
,
,
,
,
,
.
故答案为.
先根据平行线的性质,由得,再根据平行线的判定,由得,然后根据平行线的性质得,再把代入计算即可.
本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
17.【答案】
【解析】解:将方程组中两方程相加得,,
原式,
故答案为:;
由方程组得,
,
,
原式
.
由方程组两方程相加求得的值,再将原式因式分解,代值计算便可;
由方程组求得的值,再运用完全平方公式进行变换求得原式的值.
本题主要考查了解方程组,求代数式的值,完全平方公式的应用,因式分解.注意解题的技巧,是本题最大的训练目的.
18.【答案】
【解析】解:根据题意可知,能验证的公式是,
故答案为:;
,,,,
故答案为:;
.
根据阴影部分面积等于大正方形的面积减去小正方形的面积,即可得到答案;
利用所得公式即可得到答案;
利用所得公式将原式进行变形即可得到答案.
本题考查了平方差公式与几何图形,平方差公式的应用,解题关键是熟练掌握平方差公式.
19.【答案】解:如图,即为所求.
如图,即为所求.
【解析】根据轴对称的性质作图即可.
根据旋转的性质作图即可.
本题考查作图轴对称变换、旋转变换,熟练掌握轴对称和旋转的性质是解答本题的关键.
20.【答案】解:代入到原方程组中,得,可求得,
乙仅因抄错了而求得,但它仍是方程的解,
所以把代入到中得,即.
把与组成一个二元一次方程组,
解得.
故,,;
由可知原方程组为,
,得,
解得,
把代入,得,
故原方程组的解为.
【解析】所谓“方程组”的解,指的是该数值满足方程组中的每一方程的值,根据题意可得,解方程组可得原方程组中、、的值;
利用加减消元法解答即可.
此题主要考查了二元一次方程组解的定义以及解二元一次方程组的基本方法,根据方程组的解的定义列出相关方程组是解答本题的关键.
21.【答案】解:设书包的单价为元,则随身听的单价为元,
根据题意,得,
解得:,
,
答:随身听和书包的单价各是元,元;
超市需要:元;
超市需要:先购买随身听花费元,返券元,还需要元,共花费元.
因为,所以在超市购买省钱.
【解析】设随身听和书包的单价分别为元,元,根据随身听和书包单价之和是元,列方程组求解即可;
根据两商家的优惠方式分别计算是否两家都可以选择,比较钱数少的则购买更省钱.
此题主要考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
22.【答案】解:根据题意得:,
解得:,
.
答:的值为.
【解析】根据每个横行、每个竖列、每条对角线上的三个数字之和都相等,可列出关于,的二元一次方程组,解之可得出,的值,再将其代入中,即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
23.【答案】
【解析】解:,::,
,
故答案为:;
设灯转动秒,
则,,
故答案为:,;
若,
则,
又,
,
,
,
,
;
不发生变化,,理由如下:
设灯射线转动时间为秒,
,
,
又,
,而,
,
::,
即.
根据,::,即可得到的度数;
根据路程速度时间即可求出;若,则,又,所以,所以,进而求解;
设灯射线转动时间为秒,根据,,即可得出::,据此可得和关系不会变化.
本题主要考查了平行线的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.
24.【答案】解:由题意知,班和班人数相等,为:人,
班学生中测试成绩为分的人数为:人,
答:班学生中测试成绩为分的人数是人;
由题意知,;
;;
故,,的值分别为,,;
根据方差越小,数据分布越均匀可知班成绩更均匀.
【解析】根据条形图求出人数,根据扇形统计图求出所占百分比,即可得出结论;
根据中数据分别计算,,的值即可;
根据方差越小,数据分布越均匀判断即可.
本题主要考查统计的知识,熟练根据统计图得出相应的数据是解题的关键.
第1页,共1页
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. “潮涌”是年杭州亚运会会徽,钱塘江和钱江潮头是会徽的形象核心,如图是会徽的一部分,在以下四个选项中,能由该图经过平移得到的是( )
A. B.
C. D.
2. 如图,直线、相交于点,若,则的度数是( )
A.
B.
C.
D.
3. 我国古代算法统宗里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果一间客房住人,那么有人无房可住;如果一间客房住人,那么就空出一间客房,若设该店有客房间,房客人,则列出关于,的二元一次方程组正确的是( )
A. B. C. D.
4. 计算的结果是( )
A. B. C. D.
5. 如图,点在直线上,若,则的大小为 ( )
A. B. C. D.
6. 如图,已知,如果,那么的度数为( )
A.
B.
C.
D.
7. 下列因式分解正确的是( )
A. B.
C. D.
8. 某校举行“预防溺水,从我做起”演讲比赛,位评委给选手甲的评分如下:,,,,,,,则这组数据的众数和中位数分别是( )
A. , B. , C. , D. ,
9. 某次射击比赛,甲队员的成绩如图,根据此统计图,下列结论中错误的是( )
A. 最高成绩是环 B. 平均成绩是环
C. 这组成绩的众数是环 D. 这组成绩的方差是
10. 如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从出发爬到,则( )
A. 乙比甲先到
B. 甲比乙先到
C. 甲和乙同时到
D. 无法确定
二、填空题(本大题共6小题,共24.0分)
11. 如图,木棒、与分别在、处用可旋转的螺丝铆住,,,将木棒绕点逆时针旋转到与木棒平行的位置,则至少要旋转______
12. 希望村在落实“脱贫先修路”的计划中需要在家乡河上建一座桥,如图所示的方案中,在______ 处建桥最合适,理由是______ .
13. 甲、乙两名学生次立定跳远成绩的平均数相同,若甲次立定跳远成绩的方差为,乙次立定跳远成绩的方差为,则甲、乙两名学生次立定跳远成绩比较稳定的是______填“甲”或“乙”
14. 如图,将向右平移得到,如果的周长是,那么五边形的周长是______.
15. 如图,射线,,,则的度数是______ .
16. 如图,直线,,,则______.
三、解答题(本大题共8小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知关于、的二元一次方程组,则的值为______.
若,且,求的值.
18. 本小题分
如图,从边长为的大正方形中剪去一个边长为的小正方形,把剩下的阴影部分拼成如图所示的长方形.
上述操作能验证的公式是______ ;
请应用这个公式完成下列各题:
已知,,则 ______ ;
计算:.
19. 本小题分
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,的三个顶点坐标分别为,,.
画出关于轴对称的;
画出绕点逆时针旋转后得到的
20. 本小题分
甲、乙两位同学一起解方程组,甲正确地解得,乙仅因抄错了题中的,而求得.
求原方程组中,,的值.
写出求原方程组解的过程.
21. 本小题分
某同学在,两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是元,且随身听的单价比书包单价的倍少元.
求该同学看中的随身听和书包单价各是多少元?
某一天该同学上街,恰好赶上商家促销,超市所有商品打八五折销售,超市全场购物满元返购物券元销售不足元不返券,购物券全场通用,但他只带了元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
22. 本小题分
幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中把洛书用今天的数学符号翻译出来,就是一个三阶幻方如图,将个数填在三行三列的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方图的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,求的值.
23. 本小题分
“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯射线从开始顺时针旋转至便立即回转,灯射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是每秒度,灯转动的速度是每秒度,假定主道路是平行的,即,且::.
填空:______;
如图,
若灯射线先转动,灯射线才开始转动,在灯射线到达之前,设灯转动秒,则______,______;用含的式子表示
在的条件下,若,则______秒.
如图,若两灯同时转动,在灯射线到达之前.若射出的光束交于点,过作交于点,且,则在转动过程中,请探究与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
24. 本小题分
为了加强心理健康教育,某校组织七年级两班学生进行了心理健康常识测试分数为整数,满分为分,已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
求班学生中测试成绩为分的人数;
请确定下表中,,的值只要求写出求的计算过程;
统计量 平均数 众数 中位数 方差
班
班
从上表中选择合适的统计量,说明哪个班的成绩更均匀.
答案和解析
1.【答案】
【解析】
解:根据图形的平移可知:能由该图经过平移得到的是,
故选:.
【分析】本题考查了图形的平移,解决本题的关键是掌握平移的概念.
根据平移的概念即可进行判断.
2.【答案】
【解析】解:,与是对顶角,
.
故选:.
根据对顶角相等可得.
本题考查了对顶角,解题的关键是熟练掌握对顶角的性质:对顶角相等.
3.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组,根据题意得出方程组是解决问题的关键.
设该店有客房间,房客人,根据“一房七客多七客,一房九客一房空”得出方程组即可.
【解答】
解:设该店有客房间,房客人,
根据题意得:
故选:.
4.【答案】
【解析】解:原式,
故选:.
先根据积的乘方法则计算,再合并同类项.
本题主要考查了积的乘方,合并同类项,关键是熟记法则.
5.【答案】
【解析】解:因为,,
所以,
又因为,
所以,
所以,
故选:.
根据平角的定义求出的度数,再根据垂直的定义求出答案.
本题考查平角及垂直的定义,理解互相垂直的定义是解决问题的关键.
6.【答案】
【解析】解:,
.
,
.
故选D.
先根据补角的定义求出的度数,再由平行线的性质即可得出结论.
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
7.【答案】
【解析】解:选项,,故该选项不符合题意;
选项,,故该选项符合题意;
选项,,故该选项不符合题意;
选项,与没有公因式,故该选项不符合题意;
故选:.
根据因式分解的定义和因式分解常用的两种方法:提公因式法和公式法判断即可.
本题考查了因式分解,掌握是解题的关键.
8.【答案】
【解析】解:将这组数据从小到大排列为:,,,,,,,
这组数据的众数是,中位数是.
故选:.
将这组数据从小到大排列,出现次数最多的数据就是众数,处于中间位置的数就是这组数据的中位数.
本题考查了众数,中位数,掌握将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数是解题的关键.
9.【答案】
【解析】解:由题意可知,最高成绩是环,故选项A不符合题意;
平均成绩是环,故选项B不合题意;
这组成绩的众数是环,故选项C不合题意;
这组成绩的方差是,故选项D符合题意.
故选:.
根据题意分别求出这组数据的平均数、众数和方差即可判断.
此题主要考查了折线统计图,加权平均数,众数和方差,掌握平均数和方差的计算公式是解题关键.
10.【答案】
【解析】
【分析】
本题考查了生活中的平移现象,结合图形找出甲、乙两只蚂蚁的行程相等是解题的关键.
根据平移可得出两蚂蚁行程相同,结合二者速度相同即可得出结论.
【解答】
解:甲、乙两只蚂蚁的行程相同,且两只蚂蚁的速度相同,
两只蚂蚁同时到达.
故选C.
11.【答案】
【解析】解:当时,,
,,
需要变小,即将木棒绕点逆时针旋转.
故答案为:.
由平行线的判定“同位角相等,两直线平行”可知,时,,即需要变小,即将木棒绕点逆时针旋转即可.
本题主要考查平行线的性质与判定,熟知相关定理是解题基础.
12.【答案】 垂线段最短
【解析】解:,
根据垂线段最短,在处建桥最合适,
故答案为:,垂线段最短.
根据垂线段的性质得出答案.
本题考查了垂线段最短的性质,掌握垂线段最短是解题的关键.
13.【答案】乙
【解析】解:,,
,
甲、乙两名学生次立定跳远成绩的平均数相同,
甲、乙两名学生次立定跳远成绩比较稳定的是乙,
故答案为:乙.
根据方差的意义可直接求解.
此题主要考查了方差,关键是掌握方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
14.【答案】
【解析】解:向右平移得到,
,,
的周长是,即,
五边形的周长.
故答案为.
先利用平移的性质得到,,,然后利用等线段代换得到五边形的周长.
本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行或共线且相等.
15.【答案】
【解析】解:过作,
,
,
,,
,
,
,
.
故答案为:.
过作,得到,推出,,求出,得到,因此.
本题考查平行线的性质,关键是过作,得到,由平行线的性质来解决问题.
16.【答案】
【解析】解:如图,
,
,
,
,
,
.
故答案为.
先根据平行线的性质,由得,再根据平行线的判定,由得,然后根据平行线的性质得,再把代入计算即可.
本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
17.【答案】
【解析】解:将方程组中两方程相加得,,
原式,
故答案为:;
由方程组得,
,
,
原式
.
由方程组两方程相加求得的值,再将原式因式分解,代值计算便可;
由方程组求得的值,再运用完全平方公式进行变换求得原式的值.
本题主要考查了解方程组,求代数式的值,完全平方公式的应用,因式分解.注意解题的技巧,是本题最大的训练目的.
18.【答案】
【解析】解:根据题意可知,能验证的公式是,
故答案为:;
,,,,
故答案为:;
.
根据阴影部分面积等于大正方形的面积减去小正方形的面积,即可得到答案;
利用所得公式即可得到答案;
利用所得公式将原式进行变形即可得到答案.
本题考查了平方差公式与几何图形,平方差公式的应用,解题关键是熟练掌握平方差公式.
19.【答案】解:如图,即为所求.
如图,即为所求.
【解析】根据轴对称的性质作图即可.
根据旋转的性质作图即可.
本题考查作图轴对称变换、旋转变换,熟练掌握轴对称和旋转的性质是解答本题的关键.
20.【答案】解:代入到原方程组中,得,可求得,
乙仅因抄错了而求得,但它仍是方程的解,
所以把代入到中得,即.
把与组成一个二元一次方程组,
解得.
故,,;
由可知原方程组为,
,得,
解得,
把代入,得,
故原方程组的解为.
【解析】所谓“方程组”的解,指的是该数值满足方程组中的每一方程的值,根据题意可得,解方程组可得原方程组中、、的值;
利用加减消元法解答即可.
此题主要考查了二元一次方程组解的定义以及解二元一次方程组的基本方法,根据方程组的解的定义列出相关方程组是解答本题的关键.
21.【答案】解:设书包的单价为元,则随身听的单价为元,
根据题意,得,
解得:,
,
答:随身听和书包的单价各是元,元;
超市需要:元;
超市需要:先购买随身听花费元,返券元,还需要元,共花费元.
因为,所以在超市购买省钱.
【解析】设随身听和书包的单价分别为元,元,根据随身听和书包单价之和是元,列方程组求解即可;
根据两商家的优惠方式分别计算是否两家都可以选择,比较钱数少的则购买更省钱.
此题主要考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
22.【答案】解:根据题意得:,
解得:,
.
答:的值为.
【解析】根据每个横行、每个竖列、每条对角线上的三个数字之和都相等,可列出关于,的二元一次方程组,解之可得出,的值,再将其代入中,即可求出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
23.【答案】
【解析】解:,::,
,
故答案为:;
设灯转动秒,
则,,
故答案为:,;
若,
则,
又,
,
,
,
,
;
不发生变化,,理由如下:
设灯射线转动时间为秒,
,
,
又,
,而,
,
::,
即.
根据,::,即可得到的度数;
根据路程速度时间即可求出;若,则,又,所以,所以,进而求解;
设灯射线转动时间为秒,根据,,即可得出::,据此可得和关系不会变化.
本题主要考查了平行线的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.
24.【答案】解:由题意知,班和班人数相等,为:人,
班学生中测试成绩为分的人数为:人,
答:班学生中测试成绩为分的人数是人;
由题意知,;
;;
故,,的值分别为,,;
根据方差越小,数据分布越均匀可知班成绩更均匀.
【解析】根据条形图求出人数,根据扇形统计图求出所占百分比,即可得出结论;
根据中数据分别计算,,的值即可;
根据方差越小,数据分布越均匀判断即可.
本题主要考查统计的知识,熟练根据统计图得出相应的数据是解题的关键.
第1页,共1页
同课章节目录
