12.1.1 分式及分式的基本性质 课件(共21张PPT)
文档属性
| 名称 | 12.1.1 分式及分式的基本性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 07:43:26 | ||
图片预览







文档简介
(共21张PPT)
12.1.1分式及其基本性质
冀教版八年级上册
教学目标
1.理解分式的概念,能正确区分整式和分式.
2.掌握分式有意义、无意义及分式值为零的条件.(重点)
3.掌握分式的基本性质,并能够运用分式的基本性质对分式进行变形.(难点)
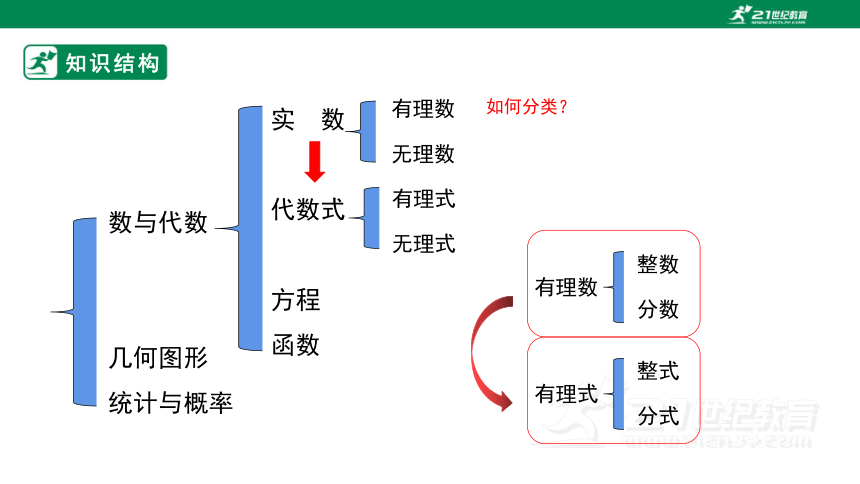
知识结构
数与代数
几何图形
统计与概率
实 数
代数式
方程
函数
有理数
无理数
如何分类?
有理数
整数
分数
有理式
无理式
有理式
整式
分式
情景引入
某种商品,原来每盒售价为p元,现在每盒的售价降低了2元.用500元钱购买这种商品,现在比原来可多买多少盒 怎样用代数式表示现在比原来可多买多少盒
2.现在每盒售价为 元;
1.原来可以买 盒;
3.现在可以买 盒;
4.现在比原来
p-2
-
新知讲解
问题 请将下列几个代数式按照你认为的共同特征进行分类,并将同一类移入一个圈内(圈的个数自己选定,若不够可再画),并说明理由.
解:
分式的概念
一
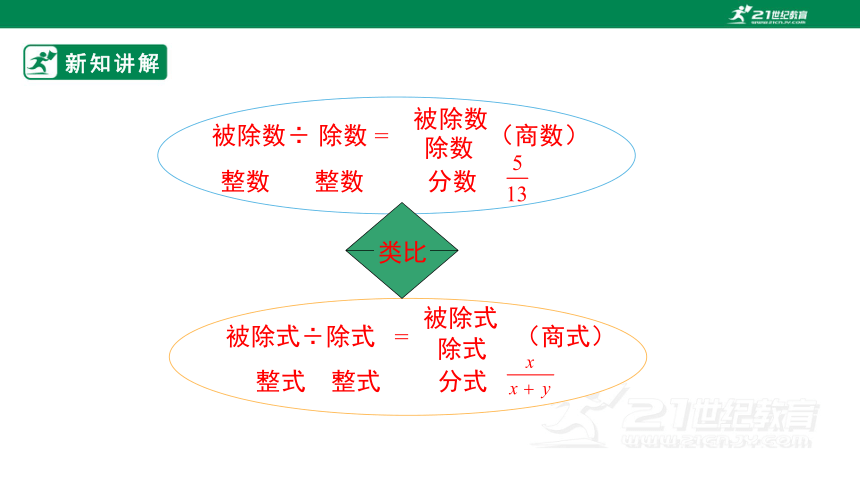
新知讲解
被除数÷ 除数 = (商数)
被除数
除数
整数 整数 分数
被除式÷除式 = (商式)
被除式
除式
类比
整式 整式 分式
新知讲解
分式的概念
一般地,我们把形如 的代数式叫做分式,其中,
A、B 都是整式,且 B 中含有字母。
A 叫做分式的分子,B 叫做分式的分母.
分式的特征是: ①分子、分母 是 ;
②分母中含有 .
字母
整式
分式的特点
都
这些是重点,要记笔记啦!
新知讲解
分式有(无)意义及分式值为 0
二
在什么情况下,下列各分式无意义 有意义?以及前两个分式值为0?
问题:
1.分数在什么情况下无意义
2.分式中分母的字母可以任意取值吗
3.在什么情况下上面的三个分式无意义
(1)分式有意义,需要分母不为0,需要解一个带“≠”的不等式;反之,当分式无意义时,则分母为0.
(2)分式的值为0,既要分子等于0,也要分母不为0.可以用方程和不等式组成条件组表示上述条件.
新知讲解
对于分式
(1) 分式无意义的条件是_____________.
(2)分式有意义的条件是 .
(3)分式的值为零的条件是 .
B = 0
B ≠ 0
B ≠ 0且 A = 0
典例精析
例 a 取何值时,分式 有意义?
解:要使得分式有意义,则 (2 + a)(3 - a)≠0,
∴2 + a ≠ 0,3 - a ≠ 0.
∴a ≠ -2,a ≠ 3.
分式有(无)意义取决于分母,当分母不等于零时分式有意义,当分母等于零时分式无意义.
注意
新知讲解
分式的基本性质
三
请看下面的问题:
分数的分子与分母同乘(或除以)一个不等于零的数,分数的值不变.
新知讲解
分式的基本性质
三
探究 你认为分式“ ”与“ ”;分式“ ”与“ ”的值相等吗?
类比分数的基本性质,你能得到分式的基本性质吗?说说看.
新知讲解
分式的基本性质
类比分数的基本性质,得到:
分式的分子与分母同乘(或除以)一个不等于零的整式 ,分式的值不变.
用公式表示为:
(其中 M 是不等于零的整式)
这些是重点,要记笔记啦!
课堂练习
1.当 a 取什么值时,分式 有意义?
2.当 y 是什么值时,分式 的值是 0?
3.当 y 是什么值时,分式 的值是 0?
a为任意实数.
y = 3.
y≠-3,y = 3.
课堂练习
4.填空:
4n
x
a2+ab
课堂练习
5.若把分式 的 和 都扩大两倍,则分式的值( )
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
6.若把分式 中的 和 都扩大 3 倍,那么分式的值( ).
A.扩大 3 倍 B.扩大 9 倍
C.扩大 4 倍 D.不变
B
A
课堂总结
①分子分母都是整式;
②分母中必含有字母.
分母中字母的取值不能使分母值为零,否则分式无意义.
当分子为零且分母不为零时,分式值为零.
分式的概念
分式的基本性质
板书设计
2.分式有意义、无意义及分式值为0的条件
1.分式的基本概念
3.分式的基本性质
12.1.1 分式及其基本性质
作业布置
【必做题】
1.教材第3页练习第1题.
2.教材第4页习题第1,2题.
【选做题】
教材第4页习题第3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.1.1分式及其基本性质
冀教版八年级上册
教学目标
1.理解分式的概念,能正确区分整式和分式.
2.掌握分式有意义、无意义及分式值为零的条件.(重点)
3.掌握分式的基本性质,并能够运用分式的基本性质对分式进行变形.(难点)
知识结构
数与代数
几何图形
统计与概率
实 数
代数式
方程
函数
有理数
无理数
如何分类?
有理数
整数
分数
有理式
无理式
有理式
整式
分式
情景引入
某种商品,原来每盒售价为p元,现在每盒的售价降低了2元.用500元钱购买这种商品,现在比原来可多买多少盒 怎样用代数式表示现在比原来可多买多少盒
2.现在每盒售价为 元;
1.原来可以买 盒;
3.现在可以买 盒;
4.现在比原来
p-2
-
新知讲解
问题 请将下列几个代数式按照你认为的共同特征进行分类,并将同一类移入一个圈内(圈的个数自己选定,若不够可再画),并说明理由.
解:
分式的概念
一
新知讲解
被除数÷ 除数 = (商数)
被除数
除数
整数 整数 分数
被除式÷除式 = (商式)
被除式
除式
类比
整式 整式 分式
新知讲解
分式的概念
一般地,我们把形如 的代数式叫做分式,其中,
A、B 都是整式,且 B 中含有字母。
A 叫做分式的分子,B 叫做分式的分母.
分式的特征是: ①分子、分母 是 ;
②分母中含有 .
字母
整式
分式的特点
都
这些是重点,要记笔记啦!
新知讲解
分式有(无)意义及分式值为 0
二
在什么情况下,下列各分式无意义 有意义?以及前两个分式值为0?
问题:
1.分数在什么情况下无意义
2.分式中分母的字母可以任意取值吗
3.在什么情况下上面的三个分式无意义
(1)分式有意义,需要分母不为0,需要解一个带“≠”的不等式;反之,当分式无意义时,则分母为0.
(2)分式的值为0,既要分子等于0,也要分母不为0.可以用方程和不等式组成条件组表示上述条件.
新知讲解
对于分式
(1) 分式无意义的条件是_____________.
(2)分式有意义的条件是 .
(3)分式的值为零的条件是 .
B = 0
B ≠ 0
B ≠ 0且 A = 0
典例精析
例 a 取何值时,分式 有意义?
解:要使得分式有意义,则 (2 + a)(3 - a)≠0,
∴2 + a ≠ 0,3 - a ≠ 0.
∴a ≠ -2,a ≠ 3.
分式有(无)意义取决于分母,当分母不等于零时分式有意义,当分母等于零时分式无意义.
注意
新知讲解
分式的基本性质
三
请看下面的问题:
分数的分子与分母同乘(或除以)一个不等于零的数,分数的值不变.
新知讲解
分式的基本性质
三
探究 你认为分式“ ”与“ ”;分式“ ”与“ ”的值相等吗?
类比分数的基本性质,你能得到分式的基本性质吗?说说看.
新知讲解
分式的基本性质
类比分数的基本性质,得到:
分式的分子与分母同乘(或除以)一个不等于零的整式 ,分式的值不变.
用公式表示为:
(其中 M 是不等于零的整式)
这些是重点,要记笔记啦!
课堂练习
1.当 a 取什么值时,分式 有意义?
2.当 y 是什么值时,分式 的值是 0?
3.当 y 是什么值时,分式 的值是 0?
a为任意实数.
y = 3.
y≠-3,y = 3.
课堂练习
4.填空:
4n
x
a2+ab
课堂练习
5.若把分式 的 和 都扩大两倍,则分式的值( )
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
6.若把分式 中的 和 都扩大 3 倍,那么分式的值( ).
A.扩大 3 倍 B.扩大 9 倍
C.扩大 4 倍 D.不变
B
A
课堂总结
①分子分母都是整式;
②分母中必含有字母.
分母中字母的取值不能使分母值为零,否则分式无意义.
当分子为零且分母不为零时,分式值为零.
分式的概念
分式的基本性质
板书设计
2.分式有意义、无意义及分式值为0的条件
1.分式的基本概念
3.分式的基本性质
12.1.1 分式及其基本性质
作业布置
【必做题】
1.教材第3页练习第1题.
2.教材第4页习题第1,2题.
【选做题】
教材第4页习题第3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
