北师大版数学八年级上册 第三章 位置与坐标2 平面直角坐标系第1课时 平面直角坐标系的有关概念导学案(含答案)
文档属性
| 名称 | 北师大版数学八年级上册 第三章 位置与坐标2 平面直角坐标系第1课时 平面直角坐标系的有关概念导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 194.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览


文档简介
第三章 位置与坐标
2 平面直角坐标系
第1课时 平面直角坐标系的有关概念
学习目标
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念.
2.认识并能画出平面直角坐标系.
3.能在给定的直角坐标系中,由点的位置写出它的坐标.
学习策略
1.学生能正确画出平面直角坐标系,并能在平面直角坐标系中,根据定义写出给定点的坐标,以及根据坐标描出点的位置.
2.理解坐标和平面上的点的一一对应的关系,体会数形结合思想.
学习过程
一情境导入:
同学们,你们喜欢旅游吗 假如你到了某一个城市旅游,那么你应怎样确定旅游景点的位置呢
下面给出一张某市旅游景点的示意图,在科技大学的小亮如何给来访的朋友介绍该市的几个风景点的位置呢 尽可能给出简洁的表示方法,并与同伴交流.
大成殿: ; 中心广场: ; 碑林: .
你是怎样确定各个景点的位置的
二.新课学习:
(1)小红在旅游示意图上画上了方格,标上数字,如图(1)所示,并用(0,0)表示科技大学的位置,用(5,7)表示中心广场的位置,那么钟楼的位置如何表示 (2,5)表示哪个地点的位置 (5,2)呢
(1) (2)
按照小红的方法,(5,2)中的2表示 ,(2,5)中的2表示 .
(2)如果小亮和他的朋友在中心广场,并以中心广场为“原点”,做了如图(2)所示的标记,那么你能表示“碑林”的位置吗 “大成殿”的位置呢 (通常将(0,0)点称为原点)
【点拨】以方格纸为背景,可以方便地利用有序数对描述各景点的位置.生活中用两个距离表示位置时,一般不用负数,而直角坐标系中的坐标是可正可负的,
1.定义:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴叫做x轴或横轴,铅直的数轴叫做y轴或纵轴,x轴和y轴统称坐标轴,它们的公共原点 O 称为直角坐标系的原点.
2.如图所示,对于平面内任意一点 P,过点 P 分别向 x 轴、y 轴作垂线,垂足在 x 轴、y 轴上对应的数 a,b 分别叫做点 P 的横坐标、纵坐标,有序数对(a,b)叫做点P 的坐标.
3.如图所示,在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分,右上方的部分叫做第一象限,其他三部分按逆时针方向依次叫做第二象限、第三象限和第四象限.坐标轴上的点不在任何一个象限内.
【注意】坐标轴上的点不属于任何象限,原点既在横轴上又在纵轴上.
在上图建立的平面直角坐标系中,两条坐标轴将坐标平面分成四个部分(按逆时针方向)分别叫第一象限、第二象限、第三象限、第四象限.
点的坐标的定义.
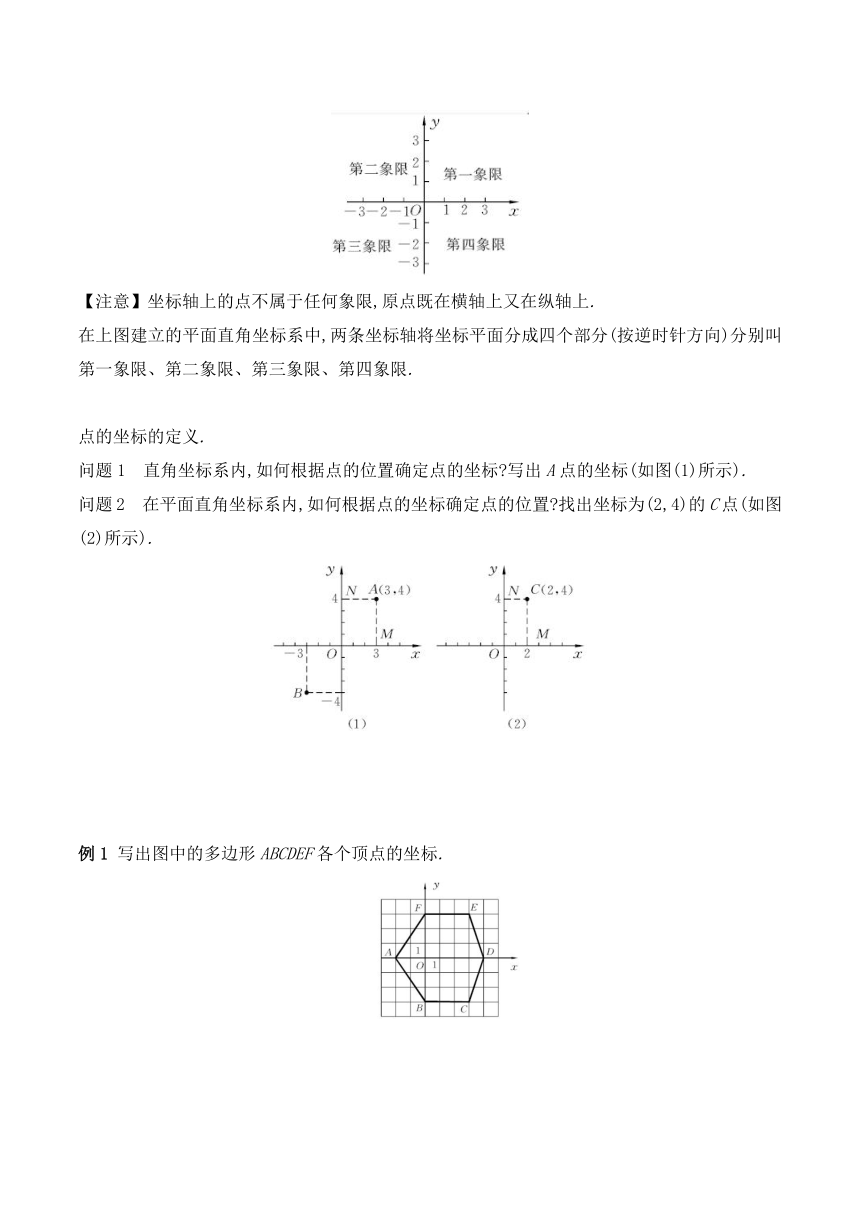
问题1 直角坐标系内,如何根据点的位置确定点的坐标 写出A点的坐标(如图(1)所示).
问题2 在平面直角坐标系内,如何根据点的坐标确定点的位置 找出坐标为(2,4)的C点(如图(2)所示).
例1 写出图中的多边形ABCDEF各个顶点的坐标.
【方法归纳】在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实数对(即点的坐标)与它对应;反过来,对于任意一对有序实数对,都有平面上唯一的一点与它对应.
三.尝试应用:
1.如图所示,分别写出点A,B,C,D,E,F,G的坐标.
四.自主总结:
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
通常两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴叫做x轴或横轴.铅直的数轴叫做y轴或纵轴.x轴和y轴统称坐标轴.它们的公共原点O称为直角坐标系的原点.如图所示,两坐标轴把平面分成四个部分,右上方的部分叫做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限.
五.达标测试
1.在平面直角坐标系中,点P(-2,3)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P(2,3)的横坐标为 ,纵坐标是 .
3.点P(0,-3)的位置是在 ( )
A.x轴的正方向上 B.x轴的负方向上 C.y轴的正方向上 D.y轴的负方向上
4.已知P(3,-2),则P点到x轴的距离为 ,到y轴的距离为 .
5.已知A点在x轴上,且OA=3,则A点的坐标为 .
6.已知A(-1,4),B(-4,4),则线段AB的长为 .
7.在如图所示的平面直角坐标系中描出A(-1,0),B(5,0),C(2,3),D(0,3)四点,并用线段将A,B,C,D四点依次连接起来,得到一个什么图形 你能求出它的面积吗
例题答案
例 解:各个顶点的坐标分别是:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3).
三.尝试应用答案
解:A(-1,-1),B(0,-3),C(2,-5),D(4,-1),E(3,2),F(-2,3),G(2,-2).
达标测试答案
1.B(解析:由象限的定义可知点P(-2,3)在第二象限.故选B.)
2.2 3
3.D(解析:横坐标为0,在y轴上,纵坐标为负数,在负半轴上.)
4.2 3(解析:点到x轴的距离为纵坐标的绝对值,到y轴的距离为横坐标的绝对值.)
5.(3,0)或(-3,0)(解析:A点在x轴上,OA=3,则A点在O点的左侧或右侧,所以A点的坐标有两个.)
6.3(解析:根据A(-1,4),B(-4,4)得AB平行于x轴,线段AB的长为A,B两点横坐标差的绝对值.)
7.解析: 把A,B,C,D四点描出来,再依次连接起来,得到一个梯形,根据面积公式可求得梯形的面积.
解:如图所示,得到一个梯形,S梯形ABCD=×(2+6)×3=12.
2 平面直角坐标系
第1课时 平面直角坐标系的有关概念
学习目标
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念.
2.认识并能画出平面直角坐标系.
3.能在给定的直角坐标系中,由点的位置写出它的坐标.
学习策略
1.学生能正确画出平面直角坐标系,并能在平面直角坐标系中,根据定义写出给定点的坐标,以及根据坐标描出点的位置.
2.理解坐标和平面上的点的一一对应的关系,体会数形结合思想.
学习过程
一情境导入:
同学们,你们喜欢旅游吗 假如你到了某一个城市旅游,那么你应怎样确定旅游景点的位置呢
下面给出一张某市旅游景点的示意图,在科技大学的小亮如何给来访的朋友介绍该市的几个风景点的位置呢 尽可能给出简洁的表示方法,并与同伴交流.
大成殿: ; 中心广场: ; 碑林: .
你是怎样确定各个景点的位置的
二.新课学习:
(1)小红在旅游示意图上画上了方格,标上数字,如图(1)所示,并用(0,0)表示科技大学的位置,用(5,7)表示中心广场的位置,那么钟楼的位置如何表示 (2,5)表示哪个地点的位置 (5,2)呢
(1) (2)
按照小红的方法,(5,2)中的2表示 ,(2,5)中的2表示 .
(2)如果小亮和他的朋友在中心广场,并以中心广场为“原点”,做了如图(2)所示的标记,那么你能表示“碑林”的位置吗 “大成殿”的位置呢 (通常将(0,0)点称为原点)
【点拨】以方格纸为背景,可以方便地利用有序数对描述各景点的位置.生活中用两个距离表示位置时,一般不用负数,而直角坐标系中的坐标是可正可负的,
1.定义:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴叫做x轴或横轴,铅直的数轴叫做y轴或纵轴,x轴和y轴统称坐标轴,它们的公共原点 O 称为直角坐标系的原点.
2.如图所示,对于平面内任意一点 P,过点 P 分别向 x 轴、y 轴作垂线,垂足在 x 轴、y 轴上对应的数 a,b 分别叫做点 P 的横坐标、纵坐标,有序数对(a,b)叫做点P 的坐标.
3.如图所示,在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分,右上方的部分叫做第一象限,其他三部分按逆时针方向依次叫做第二象限、第三象限和第四象限.坐标轴上的点不在任何一个象限内.
【注意】坐标轴上的点不属于任何象限,原点既在横轴上又在纵轴上.
在上图建立的平面直角坐标系中,两条坐标轴将坐标平面分成四个部分(按逆时针方向)分别叫第一象限、第二象限、第三象限、第四象限.
点的坐标的定义.
问题1 直角坐标系内,如何根据点的位置确定点的坐标 写出A点的坐标(如图(1)所示).
问题2 在平面直角坐标系内,如何根据点的坐标确定点的位置 找出坐标为(2,4)的C点(如图(2)所示).
例1 写出图中的多边形ABCDEF各个顶点的坐标.
【方法归纳】在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实数对(即点的坐标)与它对应;反过来,对于任意一对有序实数对,都有平面上唯一的一点与它对应.
三.尝试应用:
1.如图所示,分别写出点A,B,C,D,E,F,G的坐标.
四.自主总结:
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
通常两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴叫做x轴或横轴.铅直的数轴叫做y轴或纵轴.x轴和y轴统称坐标轴.它们的公共原点O称为直角坐标系的原点.如图所示,两坐标轴把平面分成四个部分,右上方的部分叫做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限.
五.达标测试
1.在平面直角坐标系中,点P(-2,3)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P(2,3)的横坐标为 ,纵坐标是 .
3.点P(0,-3)的位置是在 ( )
A.x轴的正方向上 B.x轴的负方向上 C.y轴的正方向上 D.y轴的负方向上
4.已知P(3,-2),则P点到x轴的距离为 ,到y轴的距离为 .
5.已知A点在x轴上,且OA=3,则A点的坐标为 .
6.已知A(-1,4),B(-4,4),则线段AB的长为 .
7.在如图所示的平面直角坐标系中描出A(-1,0),B(5,0),C(2,3),D(0,3)四点,并用线段将A,B,C,D四点依次连接起来,得到一个什么图形 你能求出它的面积吗
例题答案
例 解:各个顶点的坐标分别是:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3).
三.尝试应用答案
解:A(-1,-1),B(0,-3),C(2,-5),D(4,-1),E(3,2),F(-2,3),G(2,-2).
达标测试答案
1.B(解析:由象限的定义可知点P(-2,3)在第二象限.故选B.)
2.2 3
3.D(解析:横坐标为0,在y轴上,纵坐标为负数,在负半轴上.)
4.2 3(解析:点到x轴的距离为纵坐标的绝对值,到y轴的距离为横坐标的绝对值.)
5.(3,0)或(-3,0)(解析:A点在x轴上,OA=3,则A点在O点的左侧或右侧,所以A点的坐标有两个.)
6.3(解析:根据A(-1,4),B(-4,4)得AB平行于x轴,线段AB的长为A,B两点横坐标差的绝对值.)
7.解析: 把A,B,C,D四点描出来,再依次连接起来,得到一个梯形,根据面积公式可求得梯形的面积.
解:如图所示,得到一个梯形,S梯形ABCD=×(2+6)×3=12.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
