有三角形有关的线段(2)[下学期]
文档属性
| 名称 | 有三角形有关的线段(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 364.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-13 08:32:00 | ||
图片预览



文档简介
课件17张PPT。书生中学郑丽娇7.1.2 与三角形有关的线段(2)复习要点1.三角形的概念:由不在同一直线上的三条线段首尾顺次相接所组成的图形.3.三角形三边关系定理及推论
(1)定理:三角形任意两边之和大于第三边.
(2)推论:三角形任意两边之差小于第三边.2.三角形的顶点、角、边4.三角形的分类
1) 按边分类
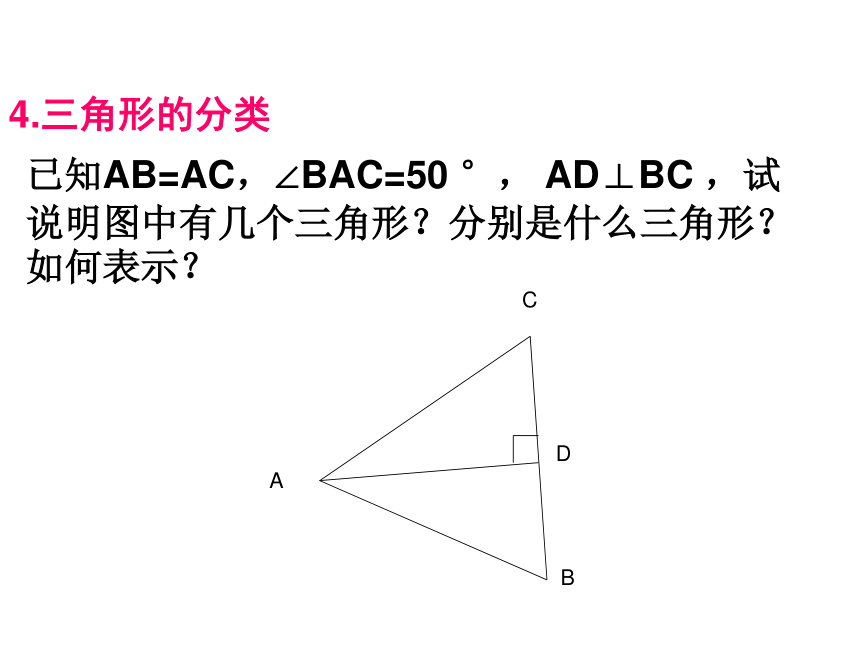
2)按角分类有一个角是直角且两条直角边是相等的三角形,我们把这个三角形叫做等腰直角三角形。已知AB=AC,∠BAC=50 °, AD⊥BC ,试说明图中有几个三角形?分别是什么三角形?如何表示?B4.三角形的分类
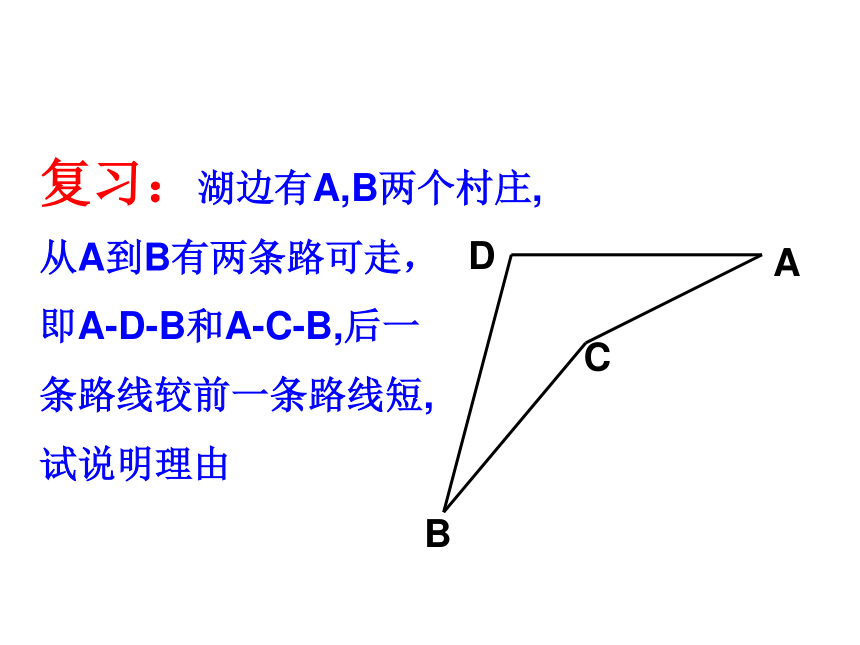
复习:湖边有A,B两个村庄,
从A到B有两条路可走,
即A-D-B和A-C-B,后一
条路线较前一条路线短,
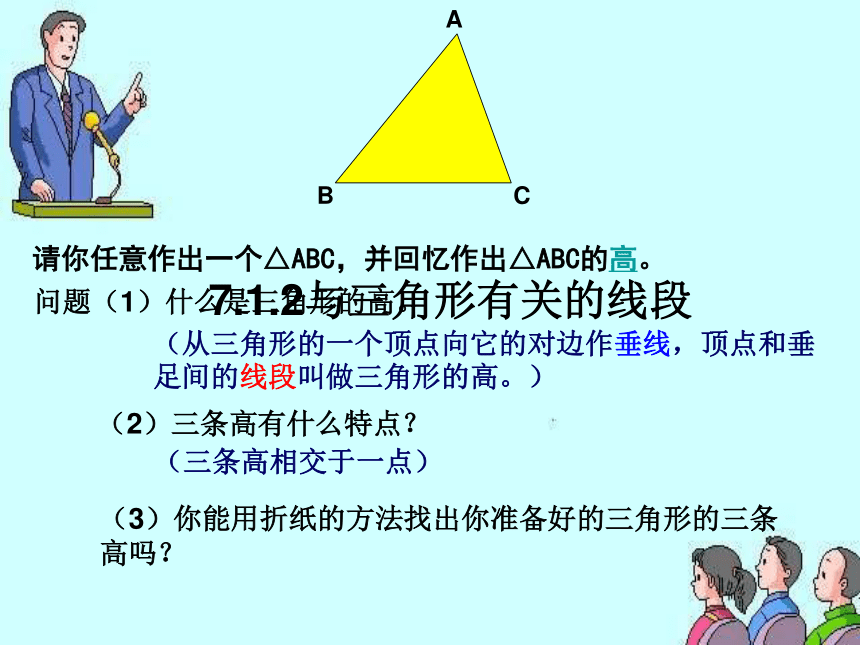
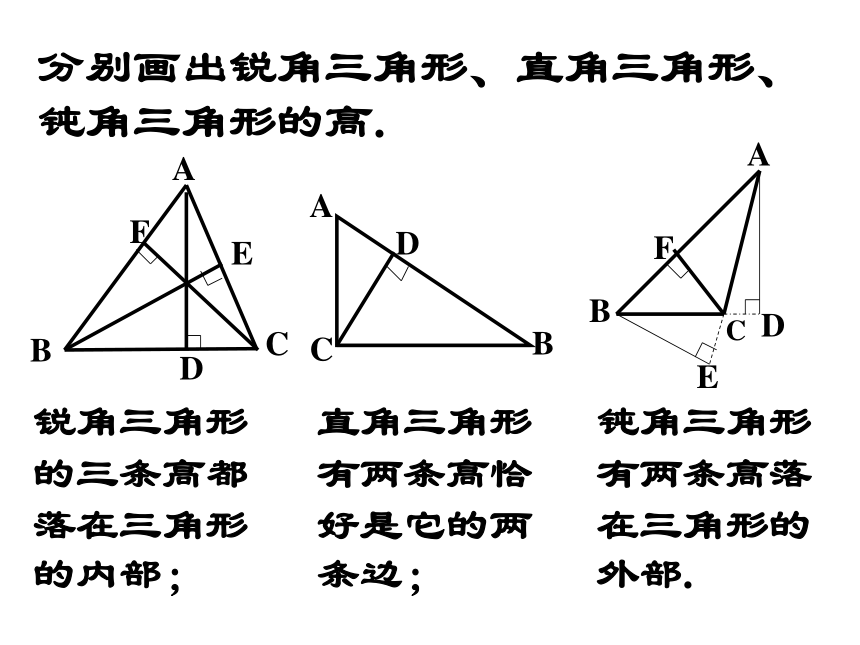
试说明理由DBCA请你任意作出一个△ABC,并回忆作出△ABC的高。 (2)三条高有什么特点?(3)你能用折纸的方法找出你准备好的三角形的三条高吗? 问题(1)什么是三角形的高。(从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高。)(三条高相交于一点)7.1.2与三角形有关的线段分别画出锐角三角形、直角三角形、钝角三角形的高.钝角三角形有两条高落在三角形的外部.锐角三角形的三条高都落在三角形的内部;直角三角形有两条高恰好是它的两条边;请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,对折,使AC与AB所在直线重合,折痕与BC交于点D。请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,把B、C重合对折,折痕与BC交于点D。(演示)问题:(1)D点有什么特殊性?(2)连接线段AD,AD把△ABC分成的两个三角形的面积有何关系?(3)请归纳线段AD的特点。 (4)你能用尺规作出中线AD吗?并用语言描述中线定义。 (点D是线段AB的中点)(两个三角形的面积相等)(在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线)问题:(1)通过这个操作你认为AD有什么位置特点?(2)你能用尺规作出AD吗?(3)请给出三角形角平分线的定义。(把∠A分成两个相等的角)(三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。)演示(1)你认为一个三角形有几条高,几条中线,几条角平分线?并分别作出来。(3)你认为“三线”定义中,高与线段垂线、三角形角平分线与角的平分线、中线与线段中点有何异同?(4)高的交点有何特别之处?(2)通过本组作出的三线,请说明它们各自的共性。巩固新知:(都有三条)(都相交于一点)(三角形的高、角平分线、中线都是线段)(锐角三角形的高的交点在三角形内,直角三角形的高的交点是两直角边的交点,钝角三角形的高的交点在三角形外)三角形的角平分线三角形的中线三角形的高三角形中的三种
重要线段:(3条)(3条)(3条)1.下列叙述:
1)三角形的高,中线,角平分线都是线段
2)三角形的高,中线,角平分线都在三角形的内部
3)三角形的高,中线,角平分线都相交于一点
4)直角三角形的高只有一条
其中叙述正确的个数是( )
A:1 B:2 C:3 D:4
2.练习:②AE是△ABC中线,那么BE= = BC。 ∠CAD∠BACCE3.如右图,D、E分别为△ABC的边AC、BC的中点,下列说法正确吗?
(1)DE是△BDC的中线。(2)BD是△ABC的中线。
(3)AD=CD,BE=EC。 (4)∠C的对边是DE。4.如右图,在△ABC中, AD是BC边上的中线,
AB-AC=3厘米,△ABD的周长为10厘米,则△ABC
的周长为多少?。拓展:在△ABC中,AB=AC,△ABC的周长为25
厘米,两边的差为2厘米,求△ABC的三边.5.已知AM是△ABC的BC边上的中线,△ABM的
周长比△ACM的周长大6厘米,且AB+AC=28厘米,
求AB,AC的长。6.如图:在△ABC中,∠ABC,
∠ACBA的平分线交于
点F,过点F作DE∥BC交
AB,AC于D,E两点,则图中
相等的角有几对?总结归纳请同学们回忆一下本课主要内容,并谈谈你有什么收获? 三线高(线)中线角平分线都是由三角形的一个顶点到对边(或对边延长线)上的点连结的线段作业教科书75页习题7.1第4、5题。再见解决问题㈡如右图,△ABC的角平分线AD、BE相交于点F,设∠C=α,请你用含α的式子表示∠AFB的度数。
(1)定理:三角形任意两边之和大于第三边.
(2)推论:三角形任意两边之差小于第三边.2.三角形的顶点、角、边4.三角形的分类
1) 按边分类
2)按角分类有一个角是直角且两条直角边是相等的三角形,我们把这个三角形叫做等腰直角三角形。已知AB=AC,∠BAC=50 °, AD⊥BC ,试说明图中有几个三角形?分别是什么三角形?如何表示?B4.三角形的分类
复习:湖边有A,B两个村庄,
从A到B有两条路可走,
即A-D-B和A-C-B,后一
条路线较前一条路线短,
试说明理由DBCA请你任意作出一个△ABC,并回忆作出△ABC的高。 (2)三条高有什么特点?(3)你能用折纸的方法找出你准备好的三角形的三条高吗? 问题(1)什么是三角形的高。(从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高。)(三条高相交于一点)7.1.2与三角形有关的线段分别画出锐角三角形、直角三角形、钝角三角形的高.钝角三角形有两条高落在三角形的外部.锐角三角形的三条高都落在三角形的内部;直角三角形有两条高恰好是它的两条边;请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,对折,使AC与AB所在直线重合,折痕与BC交于点D。请拿出你准备好的三角形纸片,在上面定义三个顶点分别为A、B、C,把B、C重合对折,折痕与BC交于点D。(演示)问题:(1)D点有什么特殊性?(2)连接线段AD,AD把△ABC分成的两个三角形的面积有何关系?(3)请归纳线段AD的特点。 (4)你能用尺规作出中线AD吗?并用语言描述中线定义。 (点D是线段AB的中点)(两个三角形的面积相等)(在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线)问题:(1)通过这个操作你认为AD有什么位置特点?(2)你能用尺规作出AD吗?(3)请给出三角形角平分线的定义。(把∠A分成两个相等的角)(三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。)演示(1)你认为一个三角形有几条高,几条中线,几条角平分线?并分别作出来。(3)你认为“三线”定义中,高与线段垂线、三角形角平分线与角的平分线、中线与线段中点有何异同?(4)高的交点有何特别之处?(2)通过本组作出的三线,请说明它们各自的共性。巩固新知:(都有三条)(都相交于一点)(三角形的高、角平分线、中线都是线段)(锐角三角形的高的交点在三角形内,直角三角形的高的交点是两直角边的交点,钝角三角形的高的交点在三角形外)三角形的角平分线三角形的中线三角形的高三角形中的三种
重要线段:(3条)(3条)(3条)1.下列叙述:
1)三角形的高,中线,角平分线都是线段
2)三角形的高,中线,角平分线都在三角形的内部
3)三角形的高,中线,角平分线都相交于一点
4)直角三角形的高只有一条
其中叙述正确的个数是( )
A:1 B:2 C:3 D:4
2.练习:②AE是△ABC中线,那么BE= = BC。 ∠CAD∠BACCE3.如右图,D、E分别为△ABC的边AC、BC的中点,下列说法正确吗?
(1)DE是△BDC的中线。(2)BD是△ABC的中线。
(3)AD=CD,BE=EC。 (4)∠C的对边是DE。4.如右图,在△ABC中, AD是BC边上的中线,
AB-AC=3厘米,△ABD的周长为10厘米,则△ABC
的周长为多少?。拓展:在△ABC中,AB=AC,△ABC的周长为25
厘米,两边的差为2厘米,求△ABC的三边.5.已知AM是△ABC的BC边上的中线,△ABM的
周长比△ACM的周长大6厘米,且AB+AC=28厘米,
求AB,AC的长。6.如图:在△ABC中,∠ABC,
∠ACBA的平分线交于
点F,过点F作DE∥BC交
AB,AC于D,E两点,则图中
相等的角有几对?总结归纳请同学们回忆一下本课主要内容,并谈谈你有什么收获? 三线高(线)中线角平分线都是由三角形的一个顶点到对边(或对边延长线)上的点连结的线段作业教科书75页习题7.1第4、5题。再见解决问题㈡如右图,△ABC的角平分线AD、BE相交于点F,设∠C=α,请你用含α的式子表示∠AFB的度数。
