【人教B版高中数学选择性必修第二册】排列、组合与二项式定理小结-课件(共40张PPT)
文档属性
| 名称 | 【人教B版高中数学选择性必修第二册】排列、组合与二项式定理小结-课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
第三章 排列、组合与二项式定理小结
高二年级 数学
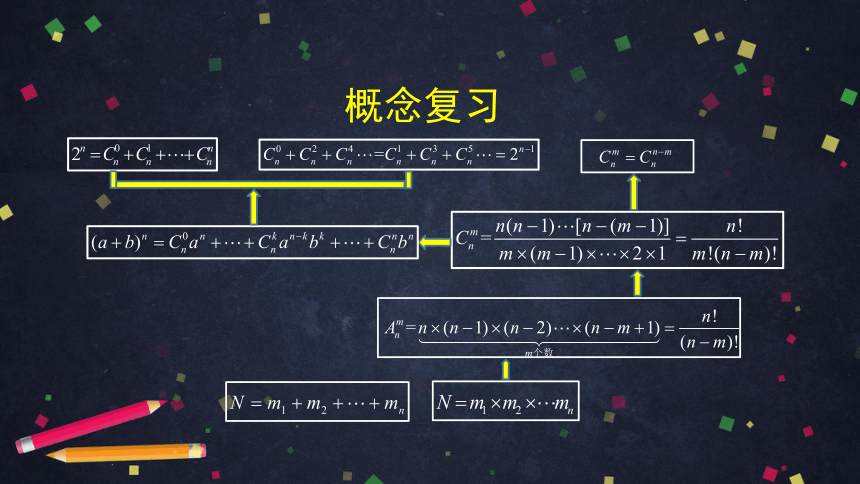
概念复习
1.分类加法计数原理:完成一件事,如果有n类办法,在第一类办法中有 种不同的方法,在第二类办法中有 种不同的方法,……,在第n类办法中有 种不同的方法,那么完成这件事共有 种不同的方法.
概念复习
2.分步乘法计数原理:完成一件事,如果需要分成n个步骤,且:做第一个步骤有 种不同的方法,做第二个步骤有 种不同的方法,……,做第n个步骤有 种不同的方法,那么完成这件事共有 种不同的方法.
概念复习
3.2.排列数:从n个不同对象中取出m(m n)个对象的所有排列的个数,称为从n个不同对象中取出m个对象的排列数,用符号 表示.m=n的排列数用符号 表示.
3.1.排列:一般地,从n个不同对象中,任取m(m n)个对象,按照一定的顺序排成一列,称为从n个不同对象中取出m个对象的一个排列.m=n的排列称为全排列.
概念复习
4.2.组合数:n个不同对象中,取出m(m n)个对象的所有组合的个数,称为从n个不同对象中取出m个对象的组合数,用符号 表示.
4.1.组合:一般地,从n个不同对象中,取出m(m n)个对象并成一组,称为从n个不同对象中取出m个对象的一个组合.
概念复习
5.二项式定理:一般地,当n是正整数时,有
概念复习
夯实基础
第一类:先从0,2中选0,0只能排在中间位置,有一种方法;再从1,3,5中任选2个数排剩下的两个位置,有 种方法,分步用乘法,共有 种方法;
例1.从0,2中选出一个数字,从1,3,5中选出两个数字,组成无重复数字的三位数,其中奇数的个数为________个.
解:解决这个问题分两类:
夯实基础
分类用加法,所以完成这件事总共有 种方法,满足条件的奇数是18 个.
第二类:再从0,2中选2,可以排在首位和第二位,有2种方法;再从1,3,5中任选2个数排剩下的两个位置,有 种方法;分步用乘法,共有 种方法.
夯实基础
总结:解决排列问题的基本方法:
1.理清完成这件事的策略
2.特殊元素、特殊位置优先排列
夯实基础
例2.张李两位老师和甲乙丙丁四位同学排成一排准备照相:
(1)若老师必须相邻,则共有多少种不同的排法;
解:把两位老师看成一个元素,加上4名同学共5个元素去排序,且两位老师之间可以交换顺序,共有 种不同排法.
夯实基础
例2.张李两位老师和甲乙丙丁四位同学排成一排准备照相:
(2)若两位老师不相邻,共有多少种不同的排法;
解:先排好4位学生,共有 种可能,4位学生共形成5个空,再把两位老师排在5个空里,就可以保证老师不相邻,因此共有 =480种不同的排法.
夯实基础
例2.张李两位老师和甲乙丙丁四位同学排成一排准备照相:
(3)又来了两个同学加入,如果保持原来6人的相对顺序不变,则不同的加入方法有多少种?
解:原来6人的相对顺序保持不变,相当于8个人排序,其中6人定序.
夯实基础
方法1:共8个位置,可以让后来的同学先选,共有 种方法,剩下6个位置,让原来的6个人保持顺序排进去,所以总共是 =56种不同的加入方法.
方法2:因为要保持之前的顺序,可以让之前的6人只选不排,所以是 种情况,接下来让后来的两人占剩下的两个位置有 种情况 ,共有 种不同的方法.
夯实基础
总结:排列中的常见问题及解决策略:
1.相邻问题——捆绑
2.不相邻问题——插空
3.定序问题——只选不排
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(1)A必须当选的选法种数;
解:A必须当选,实际上只需要从剩下的6人中还选出2人,因为是只选不排,所以是 种.
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(2)A、B都不当选的选法种数;
解:A、B都不当选,需要从剩下的5人中选出3人,所以
是 种.
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(3)男、女生至少各1人的选法种数.
典型错误解法
分析:先选出一个男生 ,再选出一个女生 ,最后随便选出一个,总共是 种 .
男甲
某女
男乙
男乙
某女
男甲
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(3)男、女生至少各1人的选法种数.
解法1:男、女生至少各1人,即1男2女,2男1女共两种情况,所以一共有 种.
解法2:用不带限制条件的组合减去全是男生和全是女生的情况即 种 .
夯实基础
总结:带限制条件的组合问题:
1.必含有
2.必不含
3.至多……,至少……
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(1)求n的值;
解:
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(2)求各项系数的和;
解:
夯实基础
即各项系数的和为0;
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(3)求含 项的系数;
解:
含 项的系数
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(4)系数最大的项是第几项?
解:
故系数最大的项是第5项.
夯实基础
总结:二项式定理常见问题及解决策略:
1.某一项的问题——
2.和的问题——
恰当赋值
难点辨析
例5.标号为1,2,3,4的4个球和3个不同的盒子,
(1)盒子不空且每个盒子只能放一个球,一共有几种方法?
解:依题意只有3个球放到盒子里,可先选球后放球,
即
种.
难点辨析
例5.标号为1,2,3,4的4个球和3个不同的盒子,
(2)4个球全部放入盒子,一共有多少种方法?
解:4个球全部放入盒子,可以从两个角度来看,一个是从球的角度,一个从盒子的角度.
难点辨析
解法1:从球的角度来看,把球放到盒子里,这件事就完成了.依次放球,放第一个球有3种方法,第2个球有3种方法,第3个球有3种方法,第4个球有3种方法,因此是
种.
难点辨析
解法2:从盒子的角度来看,可分成3类,即1个盒子得球,2个盒子得球和3个盒子得球:
第一类,4个球全部放入1个盒子,有3种.
第二类,4个球放入2个盒子,有两种情况,把球按照 或者 放到两个盒子里,前者是不均匀分组问题,而后者是均匀分组问题.
难点辨析
先看按 把球放到2个盒子的情况.
第一步:选出要放的盒子即 ,
第二步:按照非均匀分组分成两组即 ,
第三步:把分好堆的球放到选好的盒子里即 ,
总共是 种;
难点辨析
再看按 把球放到2个盒子的情况.
甲:还是先选出盒子 ,再把球分成两堆 ,最后把分好堆的球放到选好的盒子里,因此,总共是 种.
乙:先选出盒子 ,再把球分成两堆 ,最后把分好堆的球除堆的顺序后放到选好的盒子里,因此,共 种.
错误
AC,BD;BD,AC
AB,CD;CD,AB
BC,AD;AD,BC
正确
难点辨析
第三类:4个球放入3个盒子,只有1种情况,即按 放入盒子.这是部分均匀分组问题.
方法2:采用捆绑的策略.就是把2个球捆在一起当做一个球,加上剩下的2个球共3个球放入3个盒子里,即 .
方法1:仍用先分组后分盒子的策略. 即 ;
难点辨析
例5.标号为1,2,3,4的4个球和3个不同的盒子,
(2)4个球全部放入盒子,一共有多少种方法?
三类共有 种.
难点辨析
例6.相同的5个小球,放入3个不同的盒子,每个盒子至少有一个球,有多少种不同的方法?
解:相同元素的分组,只需要区分数量,用插板法.
有 种.
难点辨析
总结:1.优化解题策略
2.不同元素不均匀分组问题
3.不同元素均匀分组问题要注意除序
4.相同元素分组——插板
课堂小结
1.归纳形成体系
2.整合突破难点
课后作业
1.书架上有4本不同的数学书,5本不同的物理书,3本不同的化学书,将这些书全部竖起来排成一排;
(1)如果同类书不能分开,一共有多少种不同的排法?
(2)如果使任意两本物理书都不相邻,一共有多少种不同的排法?
课后作业
2.从10名学生中选出3人担任课代表,则甲、乙两人中至少有1人入选,而丙没有入选的不同选法共有多少种?
3.已知a是实常数,且二项式 的展开式 的系数是84,求a的值以及展开式中各项系数的和.
4.将3名医生和6名护士分配到3所学校为学生体检,每校分配1名医生和2名护士,有多少种不同的分配方案?
谢谢
第三章 排列、组合与二项式定理小结
高二年级 数学
概念复习
1.分类加法计数原理:完成一件事,如果有n类办法,在第一类办法中有 种不同的方法,在第二类办法中有 种不同的方法,……,在第n类办法中有 种不同的方法,那么完成这件事共有 种不同的方法.
概念复习
2.分步乘法计数原理:完成一件事,如果需要分成n个步骤,且:做第一个步骤有 种不同的方法,做第二个步骤有 种不同的方法,……,做第n个步骤有 种不同的方法,那么完成这件事共有 种不同的方法.
概念复习
3.2.排列数:从n个不同对象中取出m(m n)个对象的所有排列的个数,称为从n个不同对象中取出m个对象的排列数,用符号 表示.m=n的排列数用符号 表示.
3.1.排列:一般地,从n个不同对象中,任取m(m n)个对象,按照一定的顺序排成一列,称为从n个不同对象中取出m个对象的一个排列.m=n的排列称为全排列.
概念复习
4.2.组合数:n个不同对象中,取出m(m n)个对象的所有组合的个数,称为从n个不同对象中取出m个对象的组合数,用符号 表示.
4.1.组合:一般地,从n个不同对象中,取出m(m n)个对象并成一组,称为从n个不同对象中取出m个对象的一个组合.
概念复习
5.二项式定理:一般地,当n是正整数时,有
概念复习
夯实基础
第一类:先从0,2中选0,0只能排在中间位置,有一种方法;再从1,3,5中任选2个数排剩下的两个位置,有 种方法,分步用乘法,共有 种方法;
例1.从0,2中选出一个数字,从1,3,5中选出两个数字,组成无重复数字的三位数,其中奇数的个数为________个.
解:解决这个问题分两类:
夯实基础
分类用加法,所以完成这件事总共有 种方法,满足条件的奇数是18 个.
第二类:再从0,2中选2,可以排在首位和第二位,有2种方法;再从1,3,5中任选2个数排剩下的两个位置,有 种方法;分步用乘法,共有 种方法.
夯实基础
总结:解决排列问题的基本方法:
1.理清完成这件事的策略
2.特殊元素、特殊位置优先排列
夯实基础
例2.张李两位老师和甲乙丙丁四位同学排成一排准备照相:
(1)若老师必须相邻,则共有多少种不同的排法;
解:把两位老师看成一个元素,加上4名同学共5个元素去排序,且两位老师之间可以交换顺序,共有 种不同排法.
夯实基础
例2.张李两位老师和甲乙丙丁四位同学排成一排准备照相:
(2)若两位老师不相邻,共有多少种不同的排法;
解:先排好4位学生,共有 种可能,4位学生共形成5个空,再把两位老师排在5个空里,就可以保证老师不相邻,因此共有 =480种不同的排法.
夯实基础
例2.张李两位老师和甲乙丙丁四位同学排成一排准备照相:
(3)又来了两个同学加入,如果保持原来6人的相对顺序不变,则不同的加入方法有多少种?
解:原来6人的相对顺序保持不变,相当于8个人排序,其中6人定序.
夯实基础
方法1:共8个位置,可以让后来的同学先选,共有 种方法,剩下6个位置,让原来的6个人保持顺序排进去,所以总共是 =56种不同的加入方法.
方法2:因为要保持之前的顺序,可以让之前的6人只选不排,所以是 种情况,接下来让后来的两人占剩下的两个位置有 种情况 ,共有 种不同的方法.
夯实基础
总结:排列中的常见问题及解决策略:
1.相邻问题——捆绑
2.不相邻问题——插空
3.定序问题——只选不排
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(1)A必须当选的选法种数;
解:A必须当选,实际上只需要从剩下的6人中还选出2人,因为是只选不排,所以是 种.
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(2)A、B都不当选的选法种数;
解:A、B都不当选,需要从剩下的5人中选出3人,所以
是 种.
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(3)男、女生至少各1人的选法种数.
典型错误解法
分析:先选出一个男生 ,再选出一个女生 ,最后随便选出一个,总共是 种 .
男甲
某女
男乙
男乙
某女
男甲
夯实基础
例3.从3名男生4名女生中,选出3人参加某课外小组.
(3)男、女生至少各1人的选法种数.
解法1:男、女生至少各1人,即1男2女,2男1女共两种情况,所以一共有 种.
解法2:用不带限制条件的组合减去全是男生和全是女生的情况即 种 .
夯实基础
总结:带限制条件的组合问题:
1.必含有
2.必不含
3.至多……,至少……
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(1)求n的值;
解:
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(2)求各项系数的和;
解:
夯实基础
即各项系数的和为0;
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(3)求含 项的系数;
解:
含 项的系数
夯实基础
例4.已知 的展开式中,各项二项式系数和是512,
(4)系数最大的项是第几项?
解:
故系数最大的项是第5项.
夯实基础
总结:二项式定理常见问题及解决策略:
1.某一项的问题——
2.和的问题——
恰当赋值
难点辨析
例5.标号为1,2,3,4的4个球和3个不同的盒子,
(1)盒子不空且每个盒子只能放一个球,一共有几种方法?
解:依题意只有3个球放到盒子里,可先选球后放球,
即
种.
难点辨析
例5.标号为1,2,3,4的4个球和3个不同的盒子,
(2)4个球全部放入盒子,一共有多少种方法?
解:4个球全部放入盒子,可以从两个角度来看,一个是从球的角度,一个从盒子的角度.
难点辨析
解法1:从球的角度来看,把球放到盒子里,这件事就完成了.依次放球,放第一个球有3种方法,第2个球有3种方法,第3个球有3种方法,第4个球有3种方法,因此是
种.
难点辨析
解法2:从盒子的角度来看,可分成3类,即1个盒子得球,2个盒子得球和3个盒子得球:
第一类,4个球全部放入1个盒子,有3种.
第二类,4个球放入2个盒子,有两种情况,把球按照 或者 放到两个盒子里,前者是不均匀分组问题,而后者是均匀分组问题.
难点辨析
先看按 把球放到2个盒子的情况.
第一步:选出要放的盒子即 ,
第二步:按照非均匀分组分成两组即 ,
第三步:把分好堆的球放到选好的盒子里即 ,
总共是 种;
难点辨析
再看按 把球放到2个盒子的情况.
甲:还是先选出盒子 ,再把球分成两堆 ,最后把分好堆的球放到选好的盒子里,因此,总共是 种.
乙:先选出盒子 ,再把球分成两堆 ,最后把分好堆的球除堆的顺序后放到选好的盒子里,因此,共 种.
错误
AC,BD;BD,AC
AB,CD;CD,AB
BC,AD;AD,BC
正确
难点辨析
第三类:4个球放入3个盒子,只有1种情况,即按 放入盒子.这是部分均匀分组问题.
方法2:采用捆绑的策略.就是把2个球捆在一起当做一个球,加上剩下的2个球共3个球放入3个盒子里,即 .
方法1:仍用先分组后分盒子的策略. 即 ;
难点辨析
例5.标号为1,2,3,4的4个球和3个不同的盒子,
(2)4个球全部放入盒子,一共有多少种方法?
三类共有 种.
难点辨析
例6.相同的5个小球,放入3个不同的盒子,每个盒子至少有一个球,有多少种不同的方法?
解:相同元素的分组,只需要区分数量,用插板法.
有 种.
难点辨析
总结:1.优化解题策略
2.不同元素不均匀分组问题
3.不同元素均匀分组问题要注意除序
4.相同元素分组——插板
课堂小结
1.归纳形成体系
2.整合突破难点
课后作业
1.书架上有4本不同的数学书,5本不同的物理书,3本不同的化学书,将这些书全部竖起来排成一排;
(1)如果同类书不能分开,一共有多少种不同的排法?
(2)如果使任意两本物理书都不相邻,一共有多少种不同的排法?
课后作业
2.从10名学生中选出3人担任课代表,则甲、乙两人中至少有1人入选,而丙没有入选的不同选法共有多少种?
3.已知a是实常数,且二项式 的展开式 的系数是84,求a的值以及展开式中各项系数的和.
4.将3名医生和6名护士分配到3所学校为学生体检,每校分配1名医生和2名护士,有多少种不同的分配方案?
谢谢
