7.3.2多边形的内角和1[下学期]
文档属性
| 名称 | 7.3.2多边形的内角和1[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 367.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-15 09:05:00 | ||
图片预览




文档简介
课件27张PPT。欢迎指导山东省嘉祥县第四中学 曾庆坤中国第一奇村:诸葛八卦村 走一走 浙江金华兰溪诸葛八卦村
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的
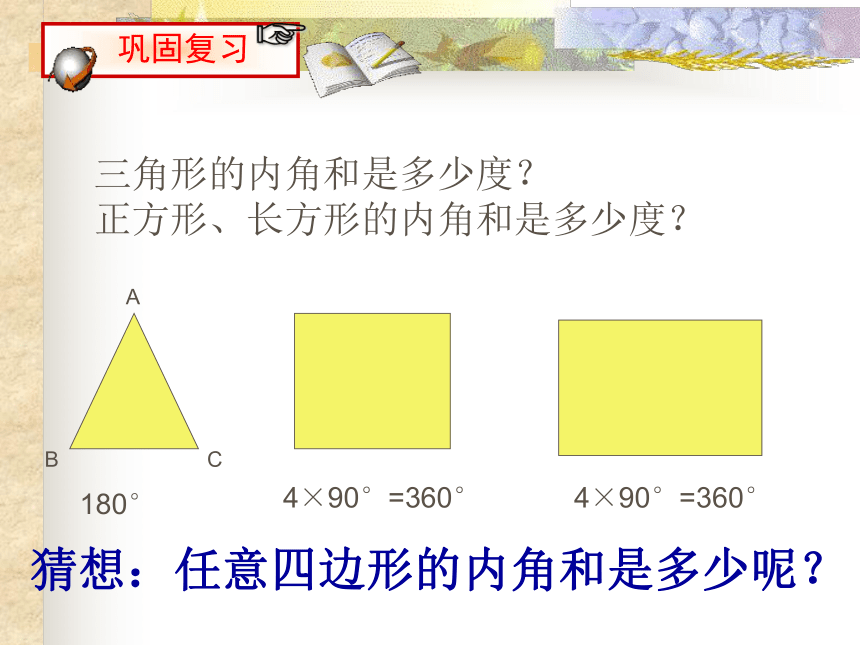
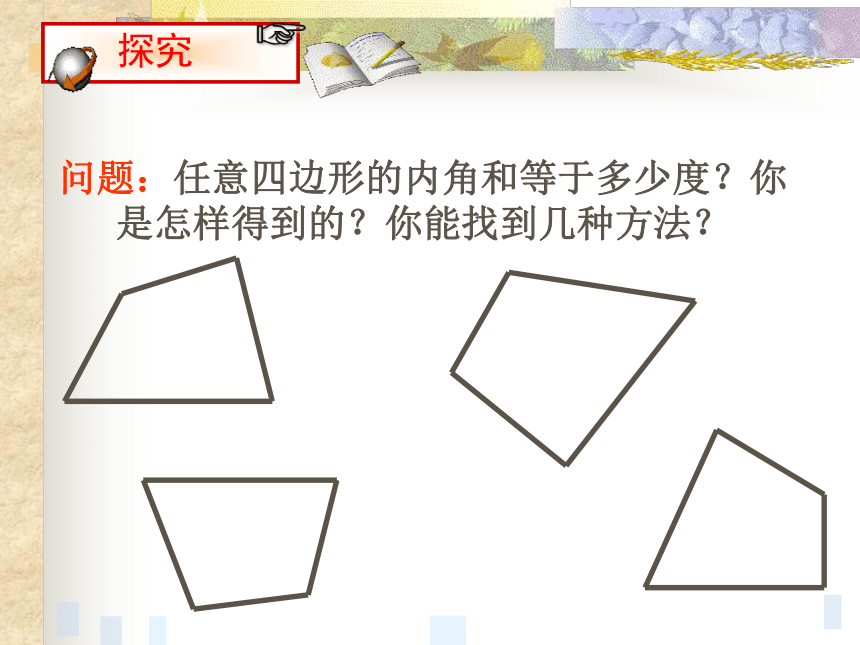
分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。 如何计算八卦图的每一个内角?7.3.2 多边形的内角和180°4×90°=360°4×90°=360°三角形的内角和是多少度? 正方形、长方形的内角和是多少度?猜想:任意四边形的内角和是多少呢?问题:任意四边形的内角和等于多少度?你是怎样得到的?你能找到几种方法?四边形内角和为3600四边形
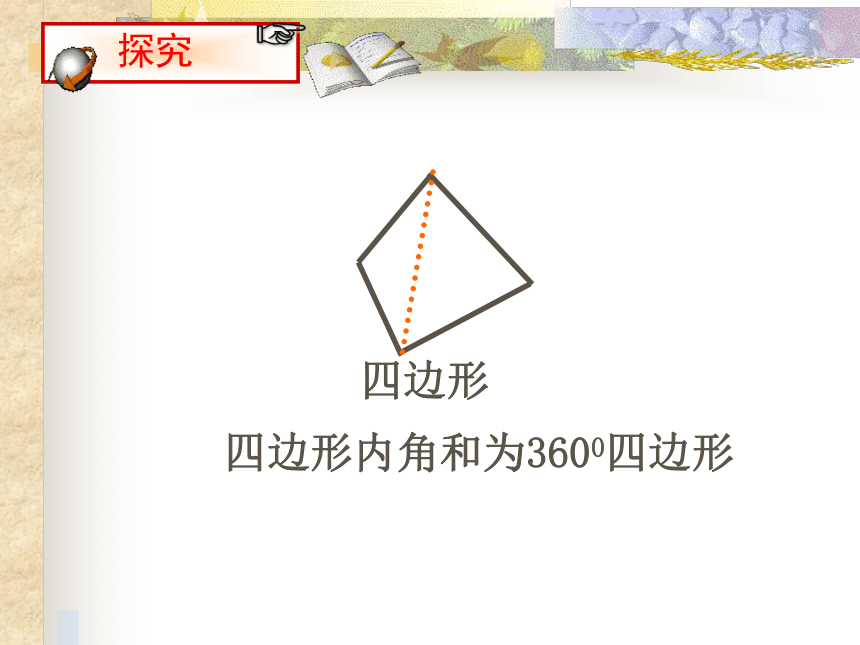
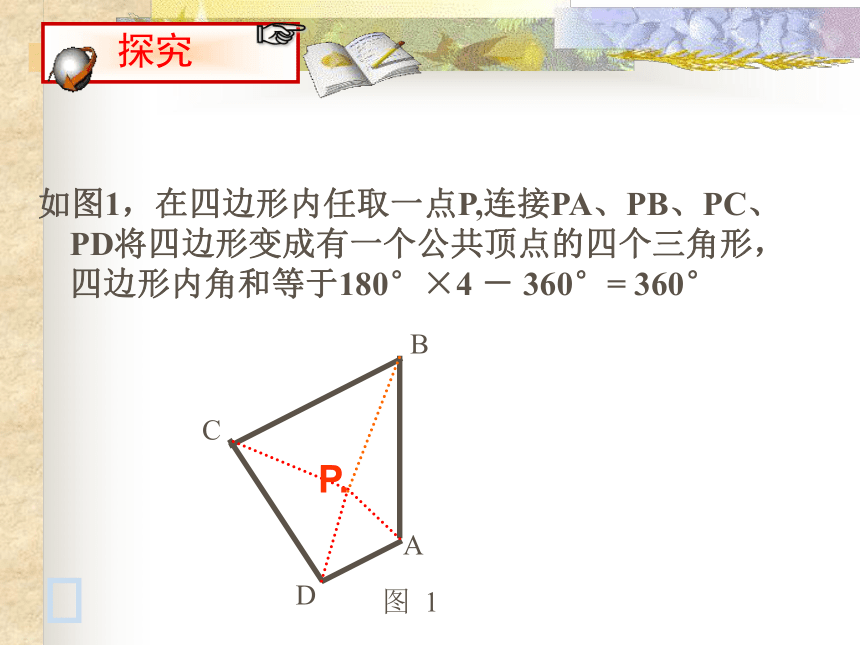
ABCD图 1如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°P.. PABDC图 2如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360° .PABCD图 3如图3,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180° ×3- 180° = 360°三角形 四边形探索多边形的内角和五边形180°360°?那n边形呢? 你能仿照四边形求内角和的方法,求出五边形、六边形的的内角和吗? 六边形?探索多边形的内角和问题:选择同一种方法分别求出任意五边形、六边形的内角和等于多少度?n边形的内角和等于 多少度? 这种探索方法你掌握了吗?请完成下表探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °720 °540 °n 边形的内角和为:(n-2)×180°探索多边形的内角和456n-1900 °720 °540 °n 边形的内角和为:(n-1)×180°-1800这种探索方法你掌握了吗?请完成下表探索多边形的内角和567 n900 °720 °540 °n 边形的内角和为:180°×n-3600这种探索方法你掌握了吗?请完成下表n边形内角和为(n-2)×1800五边形180°360°540°n边形2 x+ 140+90= 360
x=65(2)2x+x+ 90 + 120+150=(5-2)×180
x=60 (3)180-x+80+120+75=360
X=95(4) ∵ AB∥CD ∴ ∠B+∠C= 180°
∴ x+150+180+135=(5-2) ×180 ∴ x=75
(2)七边形的内角和等于 度.900(7-2)×180(3)一个多边形的内角和等于1440°,
那么这个多边形是 边形.十(4)如果一个四边形的一组对角互补,
那么另一组对角 .也互补(1)多边形的内角和随着边数的增加而 ,
边数增加一条时,它的内角和增加 度 .增 加180应用知识解决问题(1)解:如图,六边形ABCDEF中,
∠1+∠7=180 °,∠2+∠8=180 °,
∠3+∠9=180 °,∠4+∠10=180 °,
∠5+∠11=180 °,∠6+∠12=180 °.∵ ∠7+∠ 8+∠9+ ∠10 +∠11+ ∠12 =(6-2)×180 °= 720°,∴ ∠1+∠ 2+∠3+ ∠4 +∠5+ ∠6 = 6×180 °-720 ° = 360°.对于 n 边形,结论仍然成立吗?应用知识解决问题(2)n边形的外角和=n个平角-内角和
结论:多边形的外角和等于360°探究多边形的外角和=n×180°-(n-2) × 180°
=360°1.小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?2、小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得的内角和1680°。你知道该同学漏加的那个内角的度数吗?你能算出这个多边形的边数吗?
1、如图
求∠A+∠B+∠C+∠D
+∠E+∠F的度数。 122、如图,∠M1+∠M2+∠M3……+∠M6=_________
360°通过本节课的学习,你学到了哪些知识?有何体会?(1)这节课我们主要学习了多边形的内角和公式:(n-2)×180?;
(2)多边形的外角和为:3600轻轻的,我走了,正如我轻轻的来,我轻轻地点击鼠标,留下同学们的风采.
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的
分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。 如何计算八卦图的每一个内角?7.3.2 多边形的内角和180°4×90°=360°4×90°=360°三角形的内角和是多少度? 正方形、长方形的内角和是多少度?猜想:任意四边形的内角和是多少呢?问题:任意四边形的内角和等于多少度?你是怎样得到的?你能找到几种方法?四边形内角和为3600四边形
ABCD图 1如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°P.. PABDC图 2如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360° .PABCD图 3如图3,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180° ×3- 180° = 360°三角形 四边形探索多边形的内角和五边形180°360°?那n边形呢? 你能仿照四边形求内角和的方法,求出五边形、六边形的的内角和吗? 六边形?探索多边形的内角和问题:选择同一种方法分别求出任意五边形、六边形的内角和等于多少度?n边形的内角和等于 多少度? 这种探索方法你掌握了吗?请完成下表探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °720 °540 °n 边形的内角和为:(n-2)×180°探索多边形的内角和456n-1900 °720 °540 °n 边形的内角和为:(n-1)×180°-1800这种探索方法你掌握了吗?请完成下表探索多边形的内角和567 n900 °720 °540 °n 边形的内角和为:180°×n-3600这种探索方法你掌握了吗?请完成下表n边形内角和为(n-2)×1800五边形180°360°540°n边形2 x+ 140+90= 360
x=65(2)2x+x+ 90 + 120+150=(5-2)×180
x=60 (3)180-x+80+120+75=360
X=95(4) ∵ AB∥CD ∴ ∠B+∠C= 180°
∴ x+150+180+135=(5-2) ×180 ∴ x=75
(2)七边形的内角和等于 度.900(7-2)×180(3)一个多边形的内角和等于1440°,
那么这个多边形是 边形.十(4)如果一个四边形的一组对角互补,
那么另一组对角 .也互补(1)多边形的内角和随着边数的增加而 ,
边数增加一条时,它的内角和增加 度 .增 加180应用知识解决问题(1)解:如图,六边形ABCDEF中,
∠1+∠7=180 °,∠2+∠8=180 °,
∠3+∠9=180 °,∠4+∠10=180 °,
∠5+∠11=180 °,∠6+∠12=180 °.∵ ∠7+∠ 8+∠9+ ∠10 +∠11+ ∠12 =(6-2)×180 °= 720°,∴ ∠1+∠ 2+∠3+ ∠4 +∠5+ ∠6 = 6×180 °-720 ° = 360°.对于 n 边形,结论仍然成立吗?应用知识解决问题(2)n边形的外角和=n个平角-内角和
结论:多边形的外角和等于360°探究多边形的外角和=n×180°-(n-2) × 180°
=360°1.小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?2、小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得的内角和1680°。你知道该同学漏加的那个内角的度数吗?你能算出这个多边形的边数吗?
1、如图
求∠A+∠B+∠C+∠D
+∠E+∠F的度数。 122、如图,∠M1+∠M2+∠M3……+∠M6=_________
360°通过本节课的学习,你学到了哪些知识?有何体会?(1)这节课我们主要学习了多边形的内角和公式:(n-2)×180?;
(2)多边形的外角和为:3600轻轻的,我走了,正如我轻轻的来,我轻轻地点击鼠标,留下同学们的风采.
