4.2.5正态分布 课件(共27张PPT)
文档属性
| 名称 | 4.2.5正态分布 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 16:26:26 | ||
图片预览





文档简介
(共27张PPT)
正态分布
高二年级 数学
尝试与发现
已知X服从参数为100,0.5的二项分布,即X~B(100,0.5),你能手工计算出P(X=50)的值吗?
因为 ,手工计算该值是一个“几乎不可能”完成的任务,由此可以看出,若X~B(n,p),那么n较大时,直接计算P(X=k)的值将是十分困难的,有没有其他办法能得到上式的近似值呢?
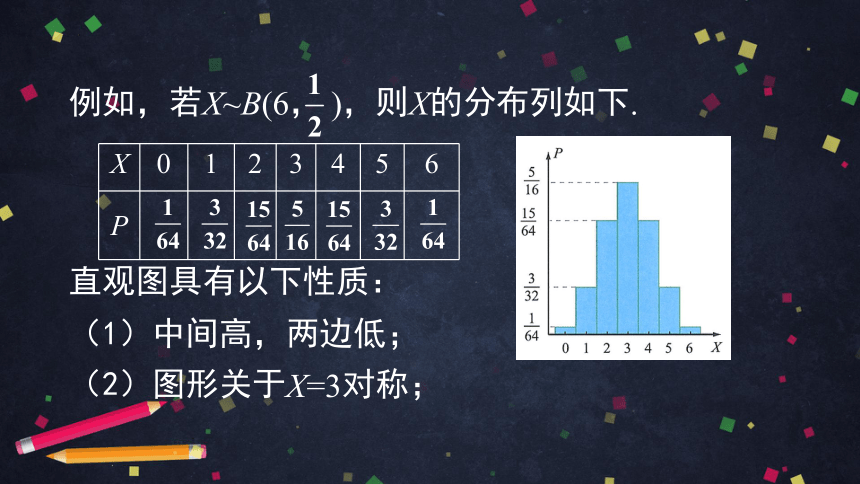
例如,若X~B(6, ),则X的分布列如下.
直观图具有以下性质:
(1)中间高,两边低;
(2)图形关于X=3对称;
X 0 1 2 3 4 5 6
P
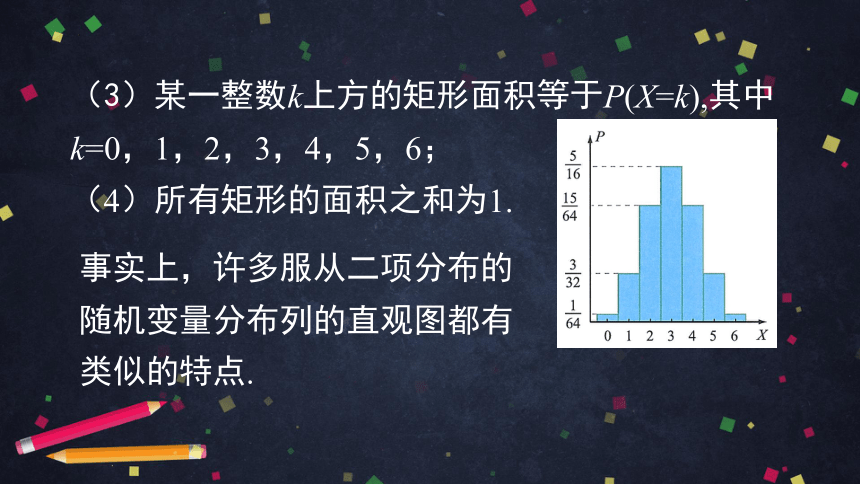
(3)某一整数k上方的矩形面积等于P(X=k),其中k=0,1,2,3,4,5,6;
(4)所有矩形的面积之和为1.
事实上,许多服从二项分布的随机变量分布列的直观图都有类似的特点.
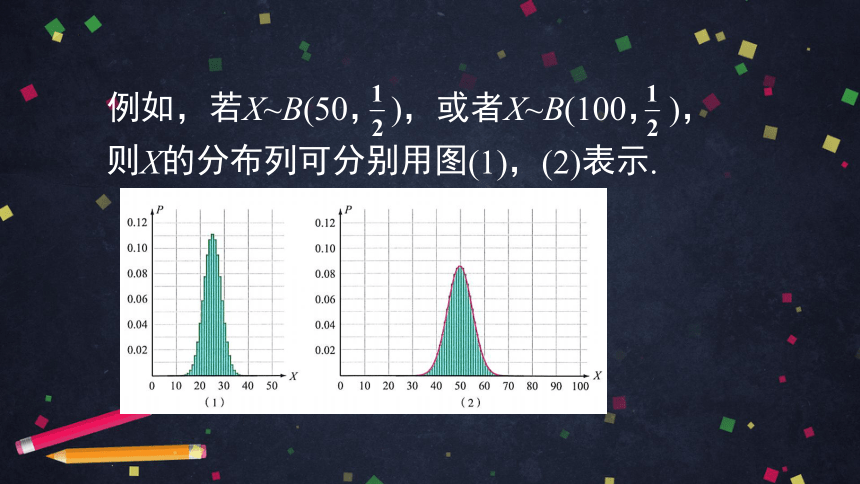
例如,若X~B(50, ),或者X~B(100, ),则X的分布列可分别用图(1),(2)表示.
其中:μ=E(X)即X的均值, ,即X的标准差。
一般地 , 对应的图像称为正态曲线.
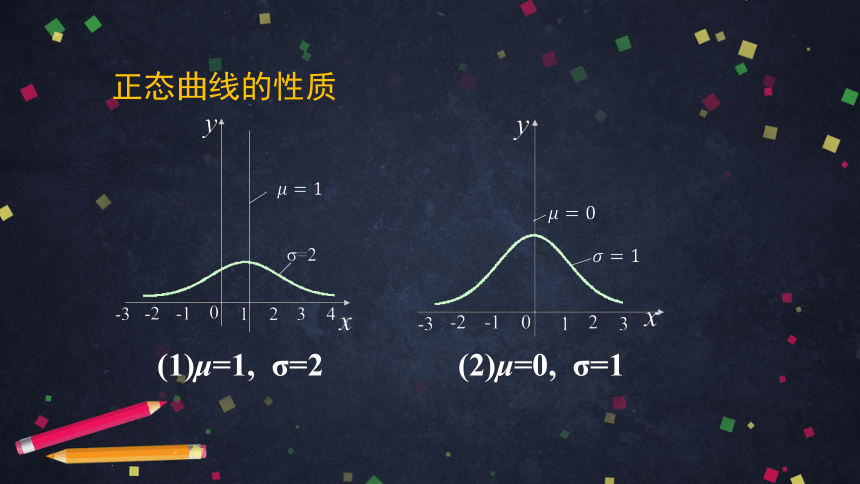
正态曲线的性质
(1)μ=1, σ=2
(2)μ=0, σ=1
正态曲线的一些性质:
(1)正态曲线关于直线 x=μ 对称,具有中间高、两边低的特点;
(2)正态曲线与x轴所围成的面积为1;
(3)σ决定曲线的“胖瘦”: σ越大,说明标准差越大,数据的集中程度越弱,所以曲线越“胖”; σ越小,曲线越“瘦”.
正态曲线与x轴在区间[μ,μ+σ]内所围面积为0.3413,在区间[μ +σ ,μ+2σ]内所围面积约为0.1359,在区间[μ+2σ,μ+3σ]内所围面积约为0.0215 ,如图所示.
例题 求正态曲线与x轴在下列区间内所围面积(精确到0.001)
(1)[μ,+∞)
解:(1)因为正态曲线关于x=μ对称,且它与x轴所围成的面积为1,所以所求面积为0.5.
(2)利用对称性可知,所求面积为
[μ,μ+σ] 内面积的2倍,即约为0.3413×2=0.6826≈0.683.
(2)[μ -σ ,μ+σ]
(3)利用对称性可知,所求面积为
(0.3413+0.1359)×2=0.9544≈0.954.
(3)[μ-2σ,μ+2σ];
(4)利用对称性可知,所求面积为
(0.3413+0.1359+0.0215)×2
=0.9974≈0.997.
(4)[μ-3σ,μ+3σ].
正态分布:如果随机变量X落在区间[a,b]内的概率,总等于 对应的正态曲线与x轴在区间[a,b]内围成的面积,则称X服从参数为μ 和σ的正态分布,记作X~N(μ ,σ2 ).
μ是X的平均值,σ是X的标准差,σ2是X的方差.
由正态曲线的性质及前面例题可知,如果X~N(μ ,σ2 ),那么
P(X≤μ )= P(X≥μ )=0.5,
P(|X –μ|≤σ)= P(μ-σ≤X≤μ+σ ) ≈68.3%,
P(|X –μ|≤2σ)= P(μ-2σ≤X≤μ+2σ ) ≈95.4%,
P(|X –μ|≤3σ)= P(μ- 3σ≤X≤μ+ 3σ ) ≈99.7%.
现实生活中,很多随机变量都服从或近似服从正态分布:随机误差、同一地区同龄人的身高、正常条件下生产出来的产品尺寸、同一批灯泡的寿命等.
例 假设某地区高二学生的身高服从正态分布,且均值为170(单位:cm,下同),标准差为10.在该地区任意抽取一名高二学生,求这名学生的身高:
(1)不高于170的概率;
解:设该学生的身高为X,X~N(170 ,102 ).(1)P(X≤170 )=50%,
(2)因为均值为170,标准差为10,而160=170-10,180=170+10,所以
P(160≤X≤ 180 ) =P(|X –170|≤10)
≈68.3%,
(2)在区间[160,180]内的概率;
(3)由(2)以及正态曲线的对称性可知
P(170≤X≤ 180 )= P(160≤X≤ 180 )
≈ 68.3%=34.15%,
由概率加法公式可知P(X≤ 180 )= P(X≤ 170 )+ P(170≤X≤ 180 )
≈ 50%+34.15%=84.15%.
(3)不高于180的概率.
标准正态分布:μ =0,σ=1的正态分布称为标准正态分布,记作X~N(0 ,1 ),对于任意a,通常记Φ(a)=P(X以下是a ≥ 0时部分Φ(a)的值:
例如:Φ(0.28)= 0.6103
例 已知X~N(0 ,1 ),利用上述表格求以下概率值:(1)P(X < 0.28);
(2)P(X <- 0.36);
解:(1)P(X < 0.28)= Φ(0.28)= 0.6103;
(2)P(X < -0.36)=Φ(-0.36)
=1-Φ(0.36)=0.3594
例 已知X~N(0 ,1 ),利用上述表格求以下概率值:(3)P(0.18≤X < 0.57);
解:(3)P(0.18≤X < 0.57)= P(X < 0.57) -P(X <0.18 )= Φ(0.57) -Φ(0.18) =0.1443.
1.二项分布与正态曲线,曲线的性质与 特点;
2.正态分布与3 原则;
3.标准正态分布.
课堂小结
设 ,则 落在 内的概率是( )
A.95.44% B.99.74%
C.4.56% D.0.26%
课后作业
谢谢
正态分布
高二年级 数学
尝试与发现
已知X服从参数为100,0.5的二项分布,即X~B(100,0.5),你能手工计算出P(X=50)的值吗?
因为 ,手工计算该值是一个“几乎不可能”完成的任务,由此可以看出,若X~B(n,p),那么n较大时,直接计算P(X=k)的值将是十分困难的,有没有其他办法能得到上式的近似值呢?
例如,若X~B(6, ),则X的分布列如下.
直观图具有以下性质:
(1)中间高,两边低;
(2)图形关于X=3对称;
X 0 1 2 3 4 5 6
P
(3)某一整数k上方的矩形面积等于P(X=k),其中k=0,1,2,3,4,5,6;
(4)所有矩形的面积之和为1.
事实上,许多服从二项分布的随机变量分布列的直观图都有类似的特点.
例如,若X~B(50, ),或者X~B(100, ),则X的分布列可分别用图(1),(2)表示.
其中:μ=E(X)即X的均值, ,即X的标准差。
一般地 , 对应的图像称为正态曲线.
正态曲线的性质
(1)μ=1, σ=2
(2)μ=0, σ=1
正态曲线的一些性质:
(1)正态曲线关于直线 x=μ 对称,具有中间高、两边低的特点;
(2)正态曲线与x轴所围成的面积为1;
(3)σ决定曲线的“胖瘦”: σ越大,说明标准差越大,数据的集中程度越弱,所以曲线越“胖”; σ越小,曲线越“瘦”.
正态曲线与x轴在区间[μ,μ+σ]内所围面积为0.3413,在区间[μ +σ ,μ+2σ]内所围面积约为0.1359,在区间[μ+2σ,μ+3σ]内所围面积约为0.0215 ,如图所示.
例题 求正态曲线与x轴在下列区间内所围面积(精确到0.001)
(1)[μ,+∞)
解:(1)因为正态曲线关于x=μ对称,且它与x轴所围成的面积为1,所以所求面积为0.5.
(2)利用对称性可知,所求面积为
[μ,μ+σ] 内面积的2倍,即约为0.3413×2=0.6826≈0.683.
(2)[μ -σ ,μ+σ]
(3)利用对称性可知,所求面积为
(0.3413+0.1359)×2=0.9544≈0.954.
(3)[μ-2σ,μ+2σ];
(4)利用对称性可知,所求面积为
(0.3413+0.1359+0.0215)×2
=0.9974≈0.997.
(4)[μ-3σ,μ+3σ].
正态分布:如果随机变量X落在区间[a,b]内的概率,总等于 对应的正态曲线与x轴在区间[a,b]内围成的面积,则称X服从参数为μ 和σ的正态分布,记作X~N(μ ,σ2 ).
μ是X的平均值,σ是X的标准差,σ2是X的方差.
由正态曲线的性质及前面例题可知,如果X~N(μ ,σ2 ),那么
P(X≤μ )= P(X≥μ )=0.5,
P(|X –μ|≤σ)= P(μ-σ≤X≤μ+σ ) ≈68.3%,
P(|X –μ|≤2σ)= P(μ-2σ≤X≤μ+2σ ) ≈95.4%,
P(|X –μ|≤3σ)= P(μ- 3σ≤X≤μ+ 3σ ) ≈99.7%.
现实生活中,很多随机变量都服从或近似服从正态分布:随机误差、同一地区同龄人的身高、正常条件下生产出来的产品尺寸、同一批灯泡的寿命等.
例 假设某地区高二学生的身高服从正态分布,且均值为170(单位:cm,下同),标准差为10.在该地区任意抽取一名高二学生,求这名学生的身高:
(1)不高于170的概率;
解:设该学生的身高为X,X~N(170 ,102 ).(1)P(X≤170 )=50%,
(2)因为均值为170,标准差为10,而160=170-10,180=170+10,所以
P(160≤X≤ 180 ) =P(|X –170|≤10)
≈68.3%,
(2)在区间[160,180]内的概率;
(3)由(2)以及正态曲线的对称性可知
P(170≤X≤ 180 )= P(160≤X≤ 180 )
≈ 68.3%=34.15%,
由概率加法公式可知P(X≤ 180 )= P(X≤ 170 )+ P(170≤X≤ 180 )
≈ 50%+34.15%=84.15%.
(3)不高于180的概率.
标准正态分布:μ =0,σ=1的正态分布称为标准正态分布,记作X~N(0 ,1 ),对于任意a,通常记Φ(a)=P(X
例如:Φ(0.28)= 0.6103
例 已知X~N(0 ,1 ),利用上述表格求以下概率值:(1)P(X < 0.28);
(2)P(X <- 0.36);
解:(1)P(X < 0.28)= Φ(0.28)= 0.6103;
(2)P(X < -0.36)=Φ(-0.36)
=1-Φ(0.36)=0.3594
例 已知X~N(0 ,1 ),利用上述表格求以下概率值:(3)P(0.18≤X < 0.57);
解:(3)P(0.18≤X < 0.57)= P(X < 0.57) -P(X <0.18 )= Φ(0.57) -Φ(0.18) =0.1443.
1.二项分布与正态曲线,曲线的性质与 特点;
2.正态分布与3 原则;
3.标准正态分布.
课堂小结
设 ,则 落在 内的概率是( )
A.95.44% B.99.74%
C.4.56% D.0.26%
课后作业
谢谢
