4.1条件概率与事件的独立性小结 课件(共33张PPT)
文档属性
| 名称 | 4.1条件概率与事件的独立性小结 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览






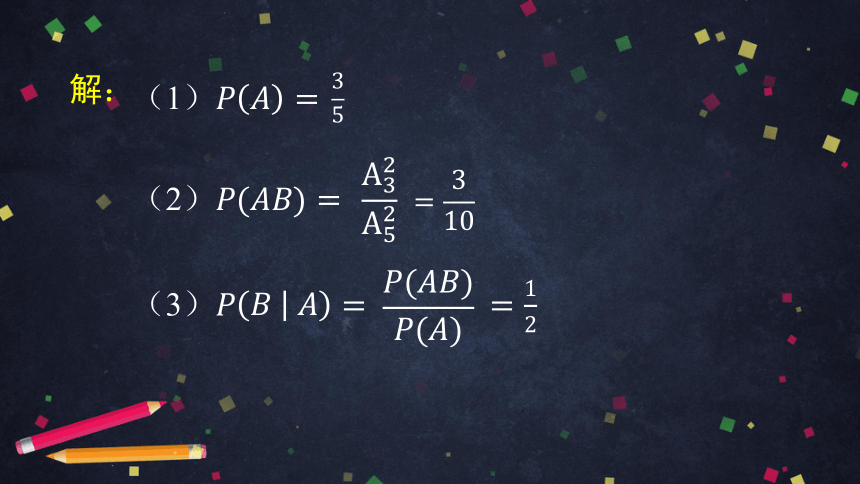




文档简介
(共33张PPT)
条件概率与事件的独立性小结
高二年级 数学
知识框架:
条件概率
条件概率公式
乘法公式
全概率公式
事件的独立性
知识梳理:
一、条件概率和乘法公式:
一般地,当事件发生的概率大于0时(即),已知__________的条件下___________的概率,称为条件概率,记作__________.
事件发生
事件发生
1.条件概率:
知识梳理:
一、条件概率和乘法公式:
2.计算公式:
3.乘法公式:
,.
知识梳理:
一、条件概率和乘法公式:
假设表示事件,,且,,则
.
推广:
例1
在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:
设“第1次抽到理科题”为事件, “第2次抽到理科题”为事件,
则第1次和第2次都抽到理科题的事件为AB,
在第1次抽到理科题的条件下,第2次抽到理科题的事件为B|A .
解:
(3)
(2)
(1)
解:
方法2
利用古典概型先求P(B |A)
再利用乘法公式求P(AB)
.
知识梳理:
二、全概率公式:
,,
.
1.全概率公式:
利用概率乘法公式、互斥加法公式
知识梳理:
若样本空间中的事件满足:
(1)任意两个事件均互斥,即;
(2);
(3).
推广:
知识梳理:
则对中的任意事件,都有,且
例2
李明早上上学的时候,可以乘坐公共汽车,也可以乘坐地铁.已知李明乘坐公共汽车的概率为0.3,乘坐地铁的概率为0.7,而且乘坐公共汽车与地铁时,李明迟到的概率分别为0.2与0.05.求李明上学迟到的概率.
分析:
“李明乘坐公共汽车”记为事件,
代入全概率公式即可求解.
则“李明乘坐地铁”为事件,
“李明上学迟到”记为事件,
则李明乘坐公共汽车迟到为事件B|A ,
李明乘坐地铁迟到为事件B| ,
解:
设“李明乘坐公共汽车”为事件,则“李明乘坐地铁”为事件,“李明上学迟到”为事件.
由全概率公式:
小结:
(1)梳理事件与事件的关系;
(2)利用数学符号表达事件及其关系;
(3)熟练运用公式求解.
知识梳理:
三、条件概率与事件独立性的关系:
1.相互独立事件:如果事件(或)是否发生对事件(或)发生的概率没有影响,这样的两个事件叫做相互独立事件.
知识梳理:
三、条件概率与事件独立性的关系:
性质:如果事件、是相互独立事件,那么与、与、与也相互独立.
知识梳理:
两个相互独立事件同时发生的概率,等于每个事件发生的概率的积.我们把两个事件、同时发生记作,则有.
2.计算公式:
事件独立的充要条件
知识梳理:
推广:如果事件相互独立,那么这个事件同时发生的概率,等于每个事件发生的概率的积.即:
.
知识梳理:
3.独立性与条件概率的关系:
当时,与独立的充要条件是:
例3
某班级的学生中,是否有外地旅游经历的人数情况如下表所示.
男生 女生
有外地旅游经历 6 9
无外地旅游经历 9 8
从这个班级中随机抽取一名学生:
(1)求抽到的人是男生的概率;
(2)求抽到的人是女生且无外地旅游经历的概率;
(3)若已知抽到的人是女生,求她有外地旅游经历的概率;
(4)判断“抽到的人是女生”与“抽到的人有外地旅游经历”是否独立.
分析:
设“抽到的人是男生”为事件,“抽到的人是女生”为事件,“抽到的人有外地旅游经历”为事件,“抽到的人无外地旅游经历”为事件.
(1)求抽到的人是男生的概率;
解:
由题意可知,
所有学生人数为,
男生人数为,
所以
(2)求抽到的人是女生且无外地旅游经历的概率;
解:
由题意可知,
所有学生人数为,
无外地旅游经历的女生人数为,
所以
(3)若已知抽到的人是女生,求她有外地旅游经历的概率;
解:
所要求的是,
所有女生人数为,
其中有外地旅游经历的人数为,
所以
也可以利用条件概率公式求解
(4)判断“抽到的人是女生”与“抽到的人有外地旅游经历”是否独立.
分析:
可以借助来判断 与是否独立.
解:
由(3)知,
由题意知,所有学生人数为,其中有外地旅游经历的学生人数为,所以.
因为,所以“抽到的人是女生”与“抽到的人有外地旅游经历”不独立.
也可判断是否P(B)
课堂小结
1.条件概率的概念及计算公式;
2.乘法公式及全概率公式;
3.事件独立性与条件概率的关系.
作业
1.分别在下列各条件下,求
(1)已知,,求;
(2)已知,,,求,.
作业
2.在一个盒子中有大小一样的15个球,其中10个红球,5个白球.甲,乙两人依次各摸出1个球.
(1)求甲得红球,乙得白球的概率;
(2)已知甲得红球,则乙得白球的概率.
谢谢
条件概率与事件的独立性小结
高二年级 数学
知识框架:
条件概率
条件概率公式
乘法公式
全概率公式
事件的独立性
知识梳理:
一、条件概率和乘法公式:
一般地,当事件发生的概率大于0时(即),已知__________的条件下___________的概率,称为条件概率,记作__________.
事件发生
事件发生
1.条件概率:
知识梳理:
一、条件概率和乘法公式:
2.计算公式:
3.乘法公式:
,.
知识梳理:
一、条件概率和乘法公式:
假设表示事件,,且,,则
.
推广:
例1
在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:
设“第1次抽到理科题”为事件, “第2次抽到理科题”为事件,
则第1次和第2次都抽到理科题的事件为AB,
在第1次抽到理科题的条件下,第2次抽到理科题的事件为B|A .
解:
(3)
(2)
(1)
解:
方法2
利用古典概型先求P(B |A)
再利用乘法公式求P(AB)
.
知识梳理:
二、全概率公式:
,,
.
1.全概率公式:
利用概率乘法公式、互斥加法公式
知识梳理:
若样本空间中的事件满足:
(1)任意两个事件均互斥,即;
(2);
(3).
推广:
知识梳理:
则对中的任意事件,都有,且
例2
李明早上上学的时候,可以乘坐公共汽车,也可以乘坐地铁.已知李明乘坐公共汽车的概率为0.3,乘坐地铁的概率为0.7,而且乘坐公共汽车与地铁时,李明迟到的概率分别为0.2与0.05.求李明上学迟到的概率.
分析:
“李明乘坐公共汽车”记为事件,
代入全概率公式即可求解.
则“李明乘坐地铁”为事件,
“李明上学迟到”记为事件,
则李明乘坐公共汽车迟到为事件B|A ,
李明乘坐地铁迟到为事件B| ,
解:
设“李明乘坐公共汽车”为事件,则“李明乘坐地铁”为事件,“李明上学迟到”为事件.
由全概率公式:
小结:
(1)梳理事件与事件的关系;
(2)利用数学符号表达事件及其关系;
(3)熟练运用公式求解.
知识梳理:
三、条件概率与事件独立性的关系:
1.相互独立事件:如果事件(或)是否发生对事件(或)发生的概率没有影响,这样的两个事件叫做相互独立事件.
知识梳理:
三、条件概率与事件独立性的关系:
性质:如果事件、是相互独立事件,那么与、与、与也相互独立.
知识梳理:
两个相互独立事件同时发生的概率,等于每个事件发生的概率的积.我们把两个事件、同时发生记作,则有.
2.计算公式:
事件独立的充要条件
知识梳理:
推广:如果事件相互独立,那么这个事件同时发生的概率,等于每个事件发生的概率的积.即:
.
知识梳理:
3.独立性与条件概率的关系:
当时,与独立的充要条件是:
例3
某班级的学生中,是否有外地旅游经历的人数情况如下表所示.
男生 女生
有外地旅游经历 6 9
无外地旅游经历 9 8
从这个班级中随机抽取一名学生:
(1)求抽到的人是男生的概率;
(2)求抽到的人是女生且无外地旅游经历的概率;
(3)若已知抽到的人是女生,求她有外地旅游经历的概率;
(4)判断“抽到的人是女生”与“抽到的人有外地旅游经历”是否独立.
分析:
设“抽到的人是男生”为事件,“抽到的人是女生”为事件,“抽到的人有外地旅游经历”为事件,“抽到的人无外地旅游经历”为事件.
(1)求抽到的人是男生的概率;
解:
由题意可知,
所有学生人数为,
男生人数为,
所以
(2)求抽到的人是女生且无外地旅游经历的概率;
解:
由题意可知,
所有学生人数为,
无外地旅游经历的女生人数为,
所以
(3)若已知抽到的人是女生,求她有外地旅游经历的概率;
解:
所要求的是,
所有女生人数为,
其中有外地旅游经历的人数为,
所以
也可以利用条件概率公式求解
(4)判断“抽到的人是女生”与“抽到的人有外地旅游经历”是否独立.
分析:
可以借助来判断 与是否独立.
解:
由(3)知,
由题意知,所有学生人数为,其中有外地旅游经历的学生人数为,所以.
因为,所以“抽到的人是女生”与“抽到的人有外地旅游经历”不独立.
也可判断是否P(B)
课堂小结
1.条件概率的概念及计算公式;
2.乘法公式及全概率公式;
3.事件独立性与条件概率的关系.
作业
1.分别在下列各条件下,求
(1)已知,,求;
(2)已知,,,求,.
作业
2.在一个盒子中有大小一样的15个球,其中10个红球,5个白球.甲,乙两人依次各摸出1个球.
(1)求甲得红球,乙得白球的概率;
(2)已知甲得红球,则乙得白球的概率.
谢谢
