4.2.2指数函数的图象和性质 课件(共35张PPT)
文档属性
| 名称 | 4.2.2指数函数的图象和性质 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 59.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 17:18:54 | ||
图片预览








文档简介
(共35张PPT)
NEW
2023 / 07
第 4 章 指数函数与对数函数
人教A版2019必修第一册
4.2.2 指数函数的图象和性质
01.
指数函数图象
03.
复合函数单调性
02.
指数函数图象的应用
目录
学习目标
1.理解指数函数的概念和意义,会画指数函数的图像。
2.探索并理解指数函数的单调性和特殊点。
3.理解指数函数的图像与性质,能运用指数函数的图像
和性质解决有关数学问题。
Topic. 01
01 情景导入
导入
问题1:你能说说研究函数的一般步骤和方法吗?
我们可以类比研究幂函数性质的过程和方法,进一步研究首先画出指数函数的图象,然后借助图象研究指数函数的性质.
问题2:函数的性质都有哪些?
定义域、值域、单调性、奇偶性、过定点……
Topic. 02
02 指数函数的图象
说明
①底数:a>0,且a≠1
②指数:自变量x
③系数:1
定义
函数 叫做指数函数,其中 x是自变量, 函数的定义域是R.
指数函数
指数函数的图象
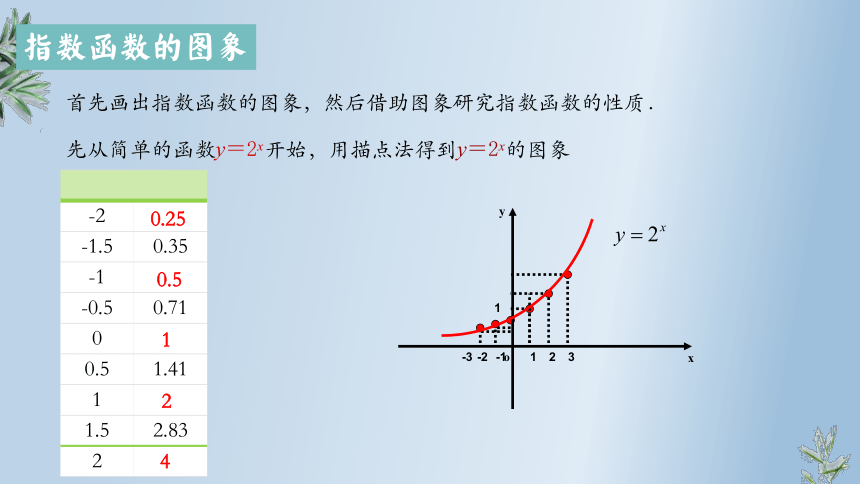
首先画出指数函数的图象,然后借助图象研究指数函数的性质.
先从简单的函数y=2x开始,用描点法得到y=2x的图象
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
0.25
0.5
1
2
4
1
x
y
o
1
2
3
-1
-2
-3
指数函数的图象
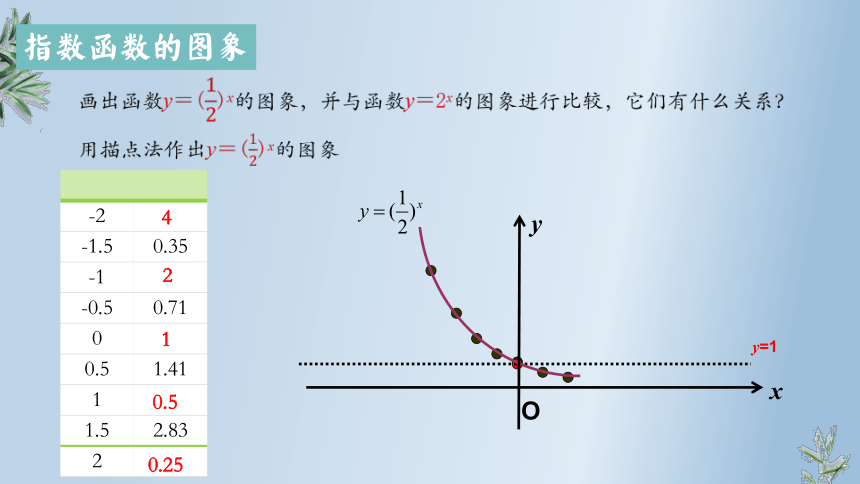
画出函数y=()x的图象,并与函数y=2x的图象进行比较,它们有什么关系?
用描点法作出y=()x的图象
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
4
2
1
0.5
0.25
y=1
x
O
y
指数函数的图象
()关于轴对称点P1()
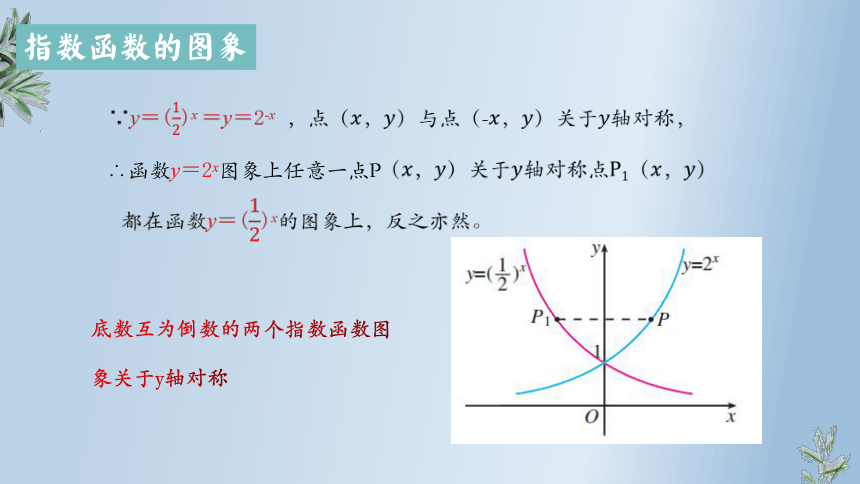
∵y=()x =y=2-x ,点()与点(-)关于轴对称,
∴函数y=2x图象上任意一点P
都在函数y=()x的图象上,反之亦然。
底数互为倒数的两个指数函数图象关于y轴对称
指数函数的图象
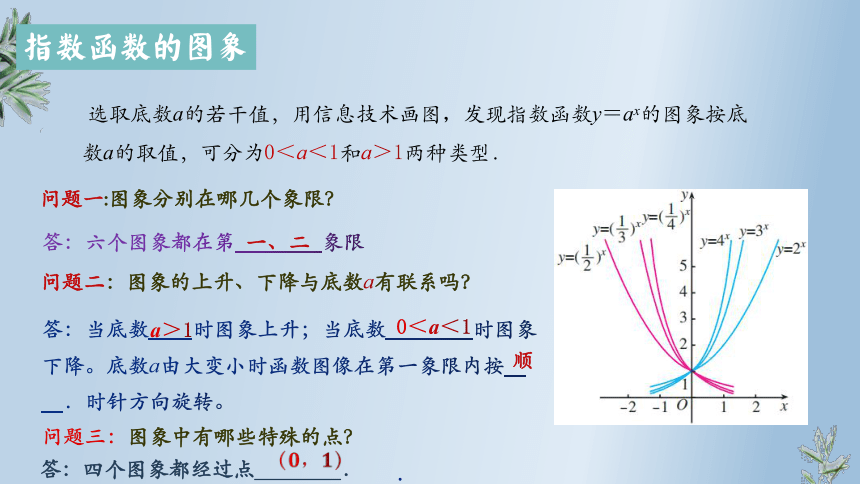
选取底数a的若干值,用信息技术画图,发现指数函数y=ax的图象按底数a的取值,可分为0<a<1和a>1两种类型.
问题一:图象分别在哪几个象限?
问题二:图象的上升、下降与底数a有联系吗?
问题三:图象中有哪些特殊的点?
答:六个图象都在第____象限
答:当底数__时图象上升;当底数____时图象下降。底数a由大变小时函数图像在第一象限内按__.时针方向旋转。
答:四个图象都经过点____.
.
一、二
a>1
0<a<1
顺
()
指数函数的图象
a>1 0<a<1
定义域为R,值域为(0,+ ).
过定点(0,1)即x=0时,y=1
在R上是增函数 在R上是减函数
当x>0时,y>1; 当x<0时,00时, 0当x<0时, y>1
非奇非偶函数
(0,1)
y=1
y
0
x
y=ax
x
y
0
y=1
y=ax
(0,1)
性质
图象
指数函数的图象
1.(a>0且a≠1)图象必过点_______
2.(a>0且a≠1)图象必过点_______
3.(a>0且a≠1)图象必过点________
(0,1)
(2,1)
(-3,0)
D
指数函数的图象
指数函数的图象
由图象可知③④的底数必大于1,①②的底数必小于1.作直线x=1,在第一象限内直线x=1与各曲线的交点的纵坐标即各指数函数的底数,则15.如图所示的是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系为( ).A.aB
指数函数的图象
6.画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.(1)y=2x+1;(2)y=-2x.
(1)y=2x+1的图象是由y=2x的图象向上平移1个单位长度得到的;(2)y=-2x的图象与y=2x的图象关于x轴对称.
指数函数的图象
7.根据函数 的图象,画出函数 的图象.
1
x
y
O
Topic. 03
03 指数函数性质的应用
指数函数性质
求指数型函数的定义域
解:(1)∴定义域为R
(2)定义域为
(3)当时,
∴当,定义域为
∴当0<,定义域为
指数函数性质
求指数型函数的定义域、值域
指数函数性质
比较大小
3.比较下列各题中两个值的大小.
解:(1)函数 是增函数,且2.5<3,则1.72.5<1.73
(3)
(2)函数 是减函数,且 ,则
指数函数性质
(1)同底数比较大小时构造指数函数,根据其单调性比较.
(2)指数相同底数不同时分别画出以两幂底数为底数的指数函数图象,当x取相同幂指数时可观察出函数值的大小.
(3)底数、指数都不相同时,取与其中一底数相同与另一指数相同的幂与两数比较,或借助“1”与两数比较.
(4)当底数含参数时,要按底数>1和0<<1两种情况分类讨论.
比较指数的大小的方法
指数函数性质
比较大小
4.比较下列两个数的大小:
指数函数性质
5.
指数函数性质
解不等式
6.
指数函数性质
解不等式
Topic. 04
04 复合函数单调性
复合函数单调性
复合函数
如果y是u的函数,而u又是x的函数,即y=f(u),u=g(x),那么y关于x的函数y=f[g(x)]叫做函数f和g的复合函数,u叫做中间变量.
复合函数单调性
内u=g(x) 增函数 减函数 增函数 减函数
外y=f(u) 增函数 减函数 减函数 增函数
复y=f[g(x)]
规律:
当内外函数的单调性相同时,其复合函数是增函数;
当内外函数的单调性不相同时,其复合函数是减函数
“同增异减”
增函数
增函数
减函数
减函数
“异”“同” 指内外函数单调性的异同
复合函数单调性
1.求函数 的单调性.
解:设 , 则
f(u)和u((x)的定义域均为R
∵u(x)在 上递减,在 上递增.
而 在R上是减函数,
∴ 在 上是增函数,在 上是减函数.
复合函数单调性
复合函数单调性
Topic. 05
05 课堂小结
课堂小结
总结:
1.指数函数的图象。
2.指数函数的应用
3.复合函数单调性
NEW
2023/ 07
感谢观看
NEW
2023 / 07
第 4 章 指数函数与对数函数
人教A版2019必修第一册
4.2.2 指数函数的图象和性质
01.
指数函数图象
03.
复合函数单调性
02.
指数函数图象的应用
目录
学习目标
1.理解指数函数的概念和意义,会画指数函数的图像。
2.探索并理解指数函数的单调性和特殊点。
3.理解指数函数的图像与性质,能运用指数函数的图像
和性质解决有关数学问题。
Topic. 01
01 情景导入
导入
问题1:你能说说研究函数的一般步骤和方法吗?
我们可以类比研究幂函数性质的过程和方法,进一步研究首先画出指数函数的图象,然后借助图象研究指数函数的性质.
问题2:函数的性质都有哪些?
定义域、值域、单调性、奇偶性、过定点……
Topic. 02
02 指数函数的图象
说明
①底数:a>0,且a≠1
②指数:自变量x
③系数:1
定义
函数 叫做指数函数,其中 x是自变量, 函数的定义域是R.
指数函数
指数函数的图象
首先画出指数函数的图象,然后借助图象研究指数函数的性质.
先从简单的函数y=2x开始,用描点法得到y=2x的图象
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
0.25
0.5
1
2
4
1
x
y
o
1
2
3
-1
-2
-3
指数函数的图象
画出函数y=()x的图象,并与函数y=2x的图象进行比较,它们有什么关系?
用描点法作出y=()x的图象
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
4
2
1
0.5
0.25
y=1
x
O
y
指数函数的图象
()关于轴对称点P1()
∵y=()x =y=2-x ,点()与点(-)关于轴对称,
∴函数y=2x图象上任意一点P
都在函数y=()x的图象上,反之亦然。
底数互为倒数的两个指数函数图象关于y轴对称
指数函数的图象
选取底数a的若干值,用信息技术画图,发现指数函数y=ax的图象按底数a的取值,可分为0<a<1和a>1两种类型.
问题一:图象分别在哪几个象限?
问题二:图象的上升、下降与底数a有联系吗?
问题三:图象中有哪些特殊的点?
答:六个图象都在第____象限
答:当底数__时图象上升;当底数____时图象下降。底数a由大变小时函数图像在第一象限内按__.时针方向旋转。
答:四个图象都经过点____.
.
一、二
a>1
0<a<1
顺
()
指数函数的图象
a>1 0<a<1
定义域为R,值域为(0,+ ).
过定点(0,1)即x=0时,y=1
在R上是增函数 在R上是减函数
当x>0时,y>1; 当x<0时,0
非奇非偶函数
(0,1)
y=1
y
0
x
y=ax
x
y
0
y=1
y=ax
(0,1)
性质
图象
指数函数的图象
1.(a>0且a≠1)图象必过点_______
2.(a>0且a≠1)图象必过点_______
3.(a>0且a≠1)图象必过点________
(0,1)
(2,1)
(-3,0)
D
指数函数的图象
指数函数的图象
由图象可知③④的底数必大于1,①②的底数必小于1.作直线x=1,在第一象限内直线x=1与各曲线的交点的纵坐标即各指数函数的底数,则1
指数函数的图象
6.画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.(1)y=2x+1;(2)y=-2x.
(1)y=2x+1的图象是由y=2x的图象向上平移1个单位长度得到的;(2)y=-2x的图象与y=2x的图象关于x轴对称.
指数函数的图象
7.根据函数 的图象,画出函数 的图象.
1
x
y
O
Topic. 03
03 指数函数性质的应用
指数函数性质
求指数型函数的定义域
解:(1)∴定义域为R
(2)定义域为
(3)当时,
∴当,定义域为
∴当0<,定义域为
指数函数性质
求指数型函数的定义域、值域
指数函数性质
比较大小
3.比较下列各题中两个值的大小.
解:(1)函数 是增函数,且2.5<3,则1.72.5<1.73
(3)
(2)函数 是减函数,且 ,则
指数函数性质
(1)同底数比较大小时构造指数函数,根据其单调性比较.
(2)指数相同底数不同时分别画出以两幂底数为底数的指数函数图象,当x取相同幂指数时可观察出函数值的大小.
(3)底数、指数都不相同时,取与其中一底数相同与另一指数相同的幂与两数比较,或借助“1”与两数比较.
(4)当底数含参数时,要按底数>1和0<<1两种情况分类讨论.
比较指数的大小的方法
指数函数性质
比较大小
4.比较下列两个数的大小:
指数函数性质
5.
指数函数性质
解不等式
6.
指数函数性质
解不等式
Topic. 04
04 复合函数单调性
复合函数单调性
复合函数
如果y是u的函数,而u又是x的函数,即y=f(u),u=g(x),那么y关于x的函数y=f[g(x)]叫做函数f和g的复合函数,u叫做中间变量.
复合函数单调性
内u=g(x) 增函数 减函数 增函数 减函数
外y=f(u) 增函数 减函数 减函数 增函数
复y=f[g(x)]
规律:
当内外函数的单调性相同时,其复合函数是增函数;
当内外函数的单调性不相同时,其复合函数是减函数
“同增异减”
增函数
增函数
减函数
减函数
“异”“同” 指内外函数单调性的异同
复合函数单调性
1.求函数 的单调性.
解:设 , 则
f(u)和u((x)的定义域均为R
∵u(x)在 上递减,在 上递增.
而 在R上是减函数,
∴ 在 上是增函数,在 上是减函数.
复合函数单调性
复合函数单调性
Topic. 05
05 课堂小结
课堂小结
总结:
1.指数函数的图象。
2.指数函数的应用
3.复合函数单调性
NEW
2023/ 07
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
