4.1.2无理数指数幂及其运算性质课件(共18张PPT)-2023-2024学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.1.2无理数指数幂及其运算性质课件(共18张PPT)-2023-2024学年高一上学期数学人教A版(2019)必修第一册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 47.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 20:58:28 | ||
图片预览






文档简介
(共18张PPT)
NEW
2023 / 07
第 4 章 指数函数与对数函数
人教A版2019必修第一册
4.1.1 n次方根与分数指数幂
01.
无理数指数幂
02.
无理数指数幂运算
目录
学习目标
1.了解指数幂由有理数扩充到无理数的过程.
2.理解指数幂的运算性质.
3.能进行指数幂(实数幂)的运算。
Topic. 01
01 情景导入
导入
目前我们将 ax (x>0)中的指数x的取值范围从整数拓展到了有理数.
当指数x是无理数时,ax 的意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质?
在初中的学习中,我们通过有理数认识了一些无理数. 类似地,也可以通过有理数指数幂来认识无理数指数幂.
导入
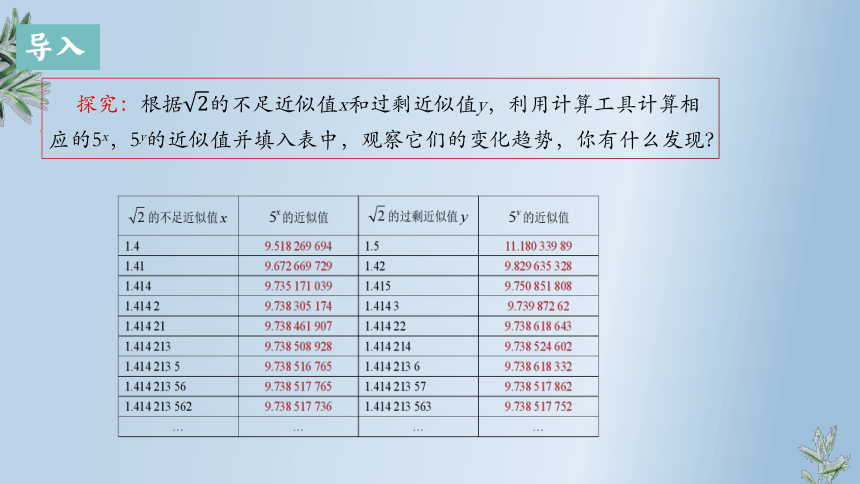
探究:根据的不足近似值x和过剩近似值y,利用计算工具计算相应的5x,5y的近似值并填入表中,观察它们的变化趋势,你有什么发现?
导入
由图表可以发现,当的不足近似值x和过剩近似值y逐渐逼近时,5x和5y都趋向于同一个数,这个数就是.也就是说,是一串逐渐增大的有理数指数幂51.4,51.41,51.414,51.4142,…和另一串逐渐减小的有理数指数幂51.5,51.42,51.415,51.4143,…逐步逼近的结果,它是一个确定的实数.
Topic. 02
02 无理数指数幂
无理数指数幂
一般地,无理数指数幂aα(a>0,α为无理数)是一个确定的实数.
定义
(1)对于无理数指数幂,我们只需要了解两点:
①它是一个确定的实数;
②它是有理数指数幂无限逼近的结果.(2)定义了无理数指数幂之后,幂的指数就由原来的有理数范围扩充到了实数范围.
说明
无理数指数幂
因此:整数指数幂的运算性质也适用于实数指数幂,即对于任意实数r,s,均有下面的运算性质.
无理数指数幂
(1)(2)正确,(3)不正确.
无理数指数幂
运用指数幂公式化简求值
无理数指数幂
进行指数幂运算时
(1)将系数、同类字母归在一起,分别计算;
(2)化负指数为正指数,
(3)化小数为分数进行运算,
从而便于进行乘除、乘方、开方运算,可以达到化繁为简的目的.
方法总结
无理数指数幂
无理数指数幂
Topic. 03
03 课堂小结
课堂小结
总结:
1.无理数指数幂。
2.无理数指数幂运算
NEW
2023/ 07
感谢观看
NEW
2023 / 07
第 4 章 指数函数与对数函数
人教A版2019必修第一册
4.1.1 n次方根与分数指数幂
01.
无理数指数幂
02.
无理数指数幂运算
目录
学习目标
1.了解指数幂由有理数扩充到无理数的过程.
2.理解指数幂的运算性质.
3.能进行指数幂(实数幂)的运算。
Topic. 01
01 情景导入
导入
目前我们将 ax (x>0)中的指数x的取值范围从整数拓展到了有理数.
当指数x是无理数时,ax 的意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质?
在初中的学习中,我们通过有理数认识了一些无理数. 类似地,也可以通过有理数指数幂来认识无理数指数幂.
导入
探究:根据的不足近似值x和过剩近似值y,利用计算工具计算相应的5x,5y的近似值并填入表中,观察它们的变化趋势,你有什么发现?
导入
由图表可以发现,当的不足近似值x和过剩近似值y逐渐逼近时,5x和5y都趋向于同一个数,这个数就是.也就是说,是一串逐渐增大的有理数指数幂51.4,51.41,51.414,51.4142,…和另一串逐渐减小的有理数指数幂51.5,51.42,51.415,51.4143,…逐步逼近的结果,它是一个确定的实数.
Topic. 02
02 无理数指数幂
无理数指数幂
一般地,无理数指数幂aα(a>0,α为无理数)是一个确定的实数.
定义
(1)对于无理数指数幂,我们只需要了解两点:
①它是一个确定的实数;
②它是有理数指数幂无限逼近的结果.(2)定义了无理数指数幂之后,幂的指数就由原来的有理数范围扩充到了实数范围.
说明
无理数指数幂
因此:整数指数幂的运算性质也适用于实数指数幂,即对于任意实数r,s,均有下面的运算性质.
无理数指数幂
(1)(2)正确,(3)不正确.
无理数指数幂
运用指数幂公式化简求值
无理数指数幂
进行指数幂运算时
(1)将系数、同类字母归在一起,分别计算;
(2)化负指数为正指数,
(3)化小数为分数进行运算,
从而便于进行乘除、乘方、开方运算,可以达到化繁为简的目的.
方法总结
无理数指数幂
无理数指数幂
Topic. 03
03 课堂小结
课堂小结
总结:
1.无理数指数幂。
2.无理数指数幂运算
NEW
2023/ 07
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
