二元一次方程式组[下学期]
文档属性
| 名称 | 二元一次方程式组[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 614.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-24 10:58:00 | ||
图片预览




文档简介
课件10张PPT。8.1 二元一次方程组
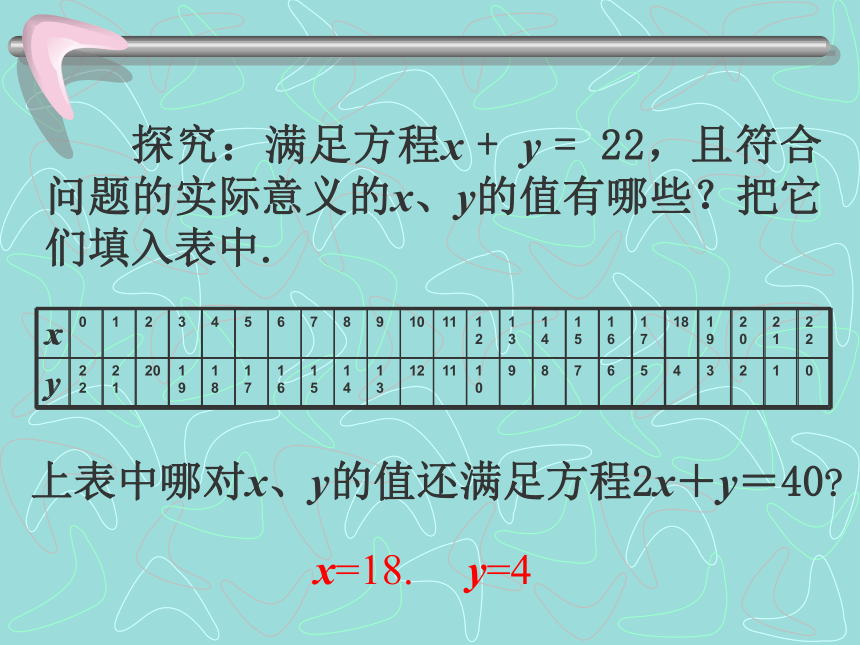
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分.负一场得1分,某队为了争取较好的名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少? 这个问题中包含了哪些必须同时满足的条件? 设胜的场数是x,负的场数是y,你能用方程把这些条件表示出来吗? 探究:满足方程x + y = 22,且符合问题的实际意义的x、y的值有哪些?把它们填入表中. 上表中哪对x、y的值还满足方程2x+y=40?x=18. y=4 一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
例1
(1)方程(a+2)x +(b-1)y = 3是二元一次方程,试求a、b的取值范围.
(2)方程x∣a∣ – 1+(a-2)y = 2是二元一次方程,试求a的值.
解:由方程是二元一次方程可知:
a+2≠0,b-1≠0;
所以a≠-2,b≠1. 例2 若方程x 2 m –1 + 5y 3n – 2 = 7是二元一次方程.求m、n的值.
例4 求二元一次方程3x+2y=19的正整数解. 课堂练习:
(1)教科书第102页练习
(2)习题8.1 1、2题 作业:
教科书第102页3、4、5题
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分.负一场得1分,某队为了争取较好的名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少? 这个问题中包含了哪些必须同时满足的条件? 设胜的场数是x,负的场数是y,你能用方程把这些条件表示出来吗? 探究:满足方程x + y = 22,且符合问题的实际意义的x、y的值有哪些?把它们填入表中. 上表中哪对x、y的值还满足方程2x+y=40?x=18. y=4 一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
例1
(1)方程(a+2)x +(b-1)y = 3是二元一次方程,试求a、b的取值范围.
(2)方程x∣a∣ – 1+(a-2)y = 2是二元一次方程,试求a的值.
解:由方程是二元一次方程可知:
a+2≠0,b-1≠0;
所以a≠-2,b≠1. 例2 若方程x 2 m –1 + 5y 3n – 2 = 7是二元一次方程.求m、n的值.
例4 求二元一次方程3x+2y=19的正整数解. 课堂练习:
(1)教科书第102页练习
(2)习题8.1 1、2题 作业:
教科书第102页3、4、5题
