4.2.2离散型随机变量的分布列课件(共44张PPT)-2022-2023学年高二下学期数学人教B版(2019)选择性必修第二册
文档属性
| 名称 | 4.2.2离散型随机变量的分布列课件(共44张PPT)-2022-2023学年高二下学期数学人教B版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览










文档简介
(共44张PPT)
离散型随机变量的分布列
高二年级 数学
复习旧知
1、离散型随机变量的分布列
一般地,当离散型随机变量的取值范围是,如果对任意概率都是已知的,则称的概率分布是已知的.
复习旧知
离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列.
复习旧知
2、离散型随机变量的分布列满足:
(1) ;
(2)
复习旧知
3、求离散型随机变量的分布列的步骤:
(1)找出离散型随机变量的所有可能值
;
(2)求出每一个值的概率
(3)列出表格.
复习旧知
在求离散型随机变量的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可验证分布列是否正确.
尝试与发现
分别写出下列各随机变量的分布列,并分析它们的共同点.
(1)篮球运动员在比赛中每次罚球得分的规则是:命中得分,不中得分,已知某篮球运动员罚球命中的概率为,设其罚球一次的得分为.
分布列为
尝试与发现
(2)假设某人寿保险的投保人年龄超过50岁的占70%,从投保人中随机抽取1人,设表示抽到年龄超过50岁的投保人人数.
分布列为
尝试与发现
(3)从含有3件次品的100件产品中随机抽取1件,设抽到的次品数为.
分布列为
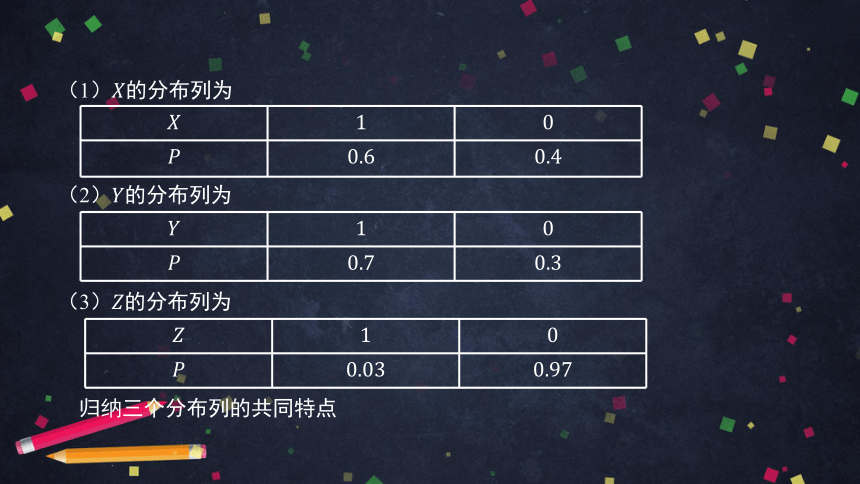
(1)分布列为
(2)分布列为
(3)分布列为
归纳三个分布列的共同特点
不难看出,上述尝试与发现中的个随机变量,它们的取值范围均为,而且分布列都能写成如下的表格形式(其中).
对于来说,,对于来说,,对于来说,.
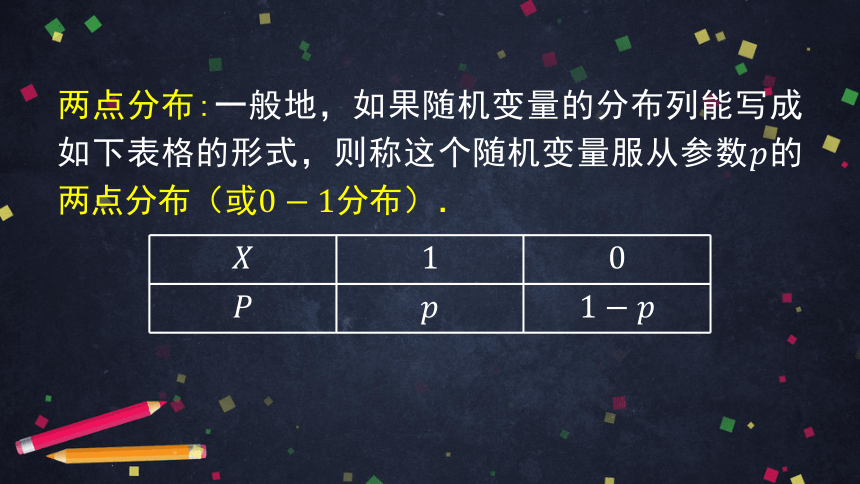
两点分布:一般地,如果随机变量的分布列能写成如下表格的形式,则称这个随机变量服从参数的两点分布(或分布).
另外,一个所有可能结果只有两种的随机试验,通常称为伯努利试验,不难看出,如果将伯努利试验的结果看成“成功”与“不成功”,并设“成功”出现的概率为,一次伯努利试验中“成功”出现的次数为,则服从参数的两点分布,因此两点分布也常称为伯努利分布,两点分布中的 也常被称为成功概率.
实例
尝试与发现中的三个试验均为伯努利试验.
日常生活中,还有很多随机试验可以看成伯努利试验:比如,观察火车是否晚点、新生婴儿的性别、考试是否及格等.
问题:只取两个不同值的随机变量是否一定服从两点分布?
不一定.如随机变量的分布列由下表给出
不服从两点分布.因为的取值不是或.
3 7
应用举例
例1 袋内有个白球,个红球,从中摸出个球,记求的分布列.
应用举例
分析:只有两个可能取值,属于两点分布,应用概率知识求出的概率,最后列出表格的形式即可.
解:
由题设可知服从两点分布.
0 1
所以的分布列为
分布列及性质的应用
例2 设随机变量的分布列为
求:
(1);
(2).
分布列及性质的应用
分析:先由分布列的性质求出
再根据, 含义,利用分布列求概率.
解:
(1) 因为 ,所以.
则
(2) 由,可得
练习
设随机变量的分布列为
求常数及相应的分布列.
解:由分布列的性质可知:
即,解得或
又因即,故.
所以,此时.
所以随机变量的分布列为:
小结
利用分布列及其性质解题时要注意以下两个问题:
(1) 的各个取值表示的事件是互斥的.
(2)不仅要注意,而且要注意
求离散型随机变量分布列
例3 口袋中有个同样大小的黑球,编号为,现从中随机取出个球,用表示取出的最大号码,求的分布列.
求离散型随机变量分布列
分析:的可能取值为,是离散型随机变量.可以利用组合数公式与古典概型概率公式求各种取值的概率.
解:随机变量的可能取值为.
从袋中随机取个球,包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为.
则有
所以随机变量的分布列为
例4 从装有个白球,个黑球和个黄球的箱中随机地取出两个球,规定每取出一个黑球赢元,而每取出一个白球输元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
解:从箱中取两个球的情形有以下种:
当取到时,结果输元,随机变量;
当取到时,输元,随机变量;
当取到时,随机变量;
当取到;
当取到;
当取到
则的可能取值为.
从而得到的分布列如下
-2 -1 0 1
小结
确定离散型随机变量的分布列的关键是要搞清取每一个值对应的随机事件,进一步利用排列、组合知识求出取每一个值的概率.
课堂小结
1、两点分布
一般地,如果随机变量的分布列能写成如下表格的形式,则称这个随机变量服从参数的两点分布(或分布).
课堂小结
2、离散型随机变量的分布列
一般地,当离散型随机变量的取值范围是,如果对任意概率都是已知的,则称的概率分布是已知的.
课堂小结
离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列.
课堂小结
3、离散型随机变量的分布列满足:
(1) ;
(2)
课后练习
教材70页 练习A 2,4;练习B 3.
A-2. 已知离散型随机变量分布列如下表所示,求值:
1 2
课后练习
A-4. 已知参数为0.3的两点分布
(1)求
(2)若,写出的分布列.
课后练习
B-3. 某射击运动员射击一次所得环数分布列如下表所示.
(1)求常数的值;
(2)求
谢谢
离散型随机变量的分布列
高二年级 数学
复习旧知
1、离散型随机变量的分布列
一般地,当离散型随机变量的取值范围是,如果对任意概率都是已知的,则称的概率分布是已知的.
复习旧知
离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列.
复习旧知
2、离散型随机变量的分布列满足:
(1) ;
(2)
复习旧知
3、求离散型随机变量的分布列的步骤:
(1)找出离散型随机变量的所有可能值
;
(2)求出每一个值的概率
(3)列出表格.
复习旧知
在求离散型随机变量的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可验证分布列是否正确.
尝试与发现
分别写出下列各随机变量的分布列,并分析它们的共同点.
(1)篮球运动员在比赛中每次罚球得分的规则是:命中得分,不中得分,已知某篮球运动员罚球命中的概率为,设其罚球一次的得分为.
分布列为
尝试与发现
(2)假设某人寿保险的投保人年龄超过50岁的占70%,从投保人中随机抽取1人,设表示抽到年龄超过50岁的投保人人数.
分布列为
尝试与发现
(3)从含有3件次品的100件产品中随机抽取1件,设抽到的次品数为.
分布列为
(1)分布列为
(2)分布列为
(3)分布列为
归纳三个分布列的共同特点
不难看出,上述尝试与发现中的个随机变量,它们的取值范围均为,而且分布列都能写成如下的表格形式(其中).
对于来说,,对于来说,,对于来说,.
两点分布:一般地,如果随机变量的分布列能写成如下表格的形式,则称这个随机变量服从参数的两点分布(或分布).
另外,一个所有可能结果只有两种的随机试验,通常称为伯努利试验,不难看出,如果将伯努利试验的结果看成“成功”与“不成功”,并设“成功”出现的概率为,一次伯努利试验中“成功”出现的次数为,则服从参数的两点分布,因此两点分布也常称为伯努利分布,两点分布中的 也常被称为成功概率.
实例
尝试与发现中的三个试验均为伯努利试验.
日常生活中,还有很多随机试验可以看成伯努利试验:比如,观察火车是否晚点、新生婴儿的性别、考试是否及格等.
问题:只取两个不同值的随机变量是否一定服从两点分布?
不一定.如随机变量的分布列由下表给出
不服从两点分布.因为的取值不是或.
3 7
应用举例
例1 袋内有个白球,个红球,从中摸出个球,记求的分布列.
应用举例
分析:只有两个可能取值,属于两点分布,应用概率知识求出的概率,最后列出表格的形式即可.
解:
由题设可知服从两点分布.
0 1
所以的分布列为
分布列及性质的应用
例2 设随机变量的分布列为
求:
(1);
(2).
分布列及性质的应用
分析:先由分布列的性质求出
再根据, 含义,利用分布列求概率.
解:
(1) 因为 ,所以.
则
(2) 由,可得
练习
设随机变量的分布列为
求常数及相应的分布列.
解:由分布列的性质可知:
即,解得或
又因即,故.
所以,此时.
所以随机变量的分布列为:
小结
利用分布列及其性质解题时要注意以下两个问题:
(1) 的各个取值表示的事件是互斥的.
(2)不仅要注意,而且要注意
求离散型随机变量分布列
例3 口袋中有个同样大小的黑球,编号为,现从中随机取出个球,用表示取出的最大号码,求的分布列.
求离散型随机变量分布列
分析:的可能取值为,是离散型随机变量.可以利用组合数公式与古典概型概率公式求各种取值的概率.
解:随机变量的可能取值为.
从袋中随机取个球,包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为.
则有
所以随机变量的分布列为
例4 从装有个白球,个黑球和个黄球的箱中随机地取出两个球,规定每取出一个黑球赢元,而每取出一个白球输元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
解:从箱中取两个球的情形有以下种:
当取到时,结果输元,随机变量;
当取到时,输元,随机变量;
当取到时,随机变量;
当取到;
当取到;
当取到
则的可能取值为.
从而得到的分布列如下
-2 -1 0 1
小结
确定离散型随机变量的分布列的关键是要搞清取每一个值对应的随机事件,进一步利用排列、组合知识求出取每一个值的概率.
课堂小结
1、两点分布
一般地,如果随机变量的分布列能写成如下表格的形式,则称这个随机变量服从参数的两点分布(或分布).
课堂小结
2、离散型随机变量的分布列
一般地,当离散型随机变量的取值范围是,如果对任意概率都是已知的,则称的概率分布是已知的.
课堂小结
离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列.
课堂小结
3、离散型随机变量的分布列满足:
(1) ;
(2)
课后练习
教材70页 练习A 2,4;练习B 3.
A-2. 已知离散型随机变量分布列如下表所示,求值:
1 2
课后练习
A-4. 已知参数为0.3的两点分布
(1)求
(2)若,写出的分布列.
课后练习
B-3. 某射击运动员射击一次所得环数分布列如下表所示.
(1)求常数的值;
(2)求
谢谢
