4.1.3独立性与条件概率的关系课件(共37张PPT)-2022-2023学年高二上学期数学人教B版(2019)选择性必修第二册
文档属性
| 名称 | 4.1.3独立性与条件概率的关系课件(共37张PPT)-2022-2023学年高二上学期数学人教B版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 21:10:38 | ||
图片预览











文档简介
(共37张PPT)
独立性与条件概率的关系
高二年级 数学
知识回顾:
1.条件概率的概念和计算公式是什么?
一般地,当事件发生的概率大于0时(即),已知事件发生的条件下事件发生的概率,称为条件概率,记作.
知识回顾:
2.事件与事件相互独立的充要条件是什么?
知识回顾:
3.事件与事件独立的直观理解是什么?
事件是否发生不会影响事件发生的概率,事件是否发生也不会影响事件发生的概率.
思考:
事件与事件独立的直观理解的数学含义是什么?
尝试与探究:
假设且,在与独立的前提下,通过条件概率的计算公式考察与的关系,以及与的关系.
分析:
当且时,由条件概率的计算公式有
分析:
类似地,可以看出,如果,那么一定有
.
事件独立的充要条件:
当时,与独立的充要条件是:
例1
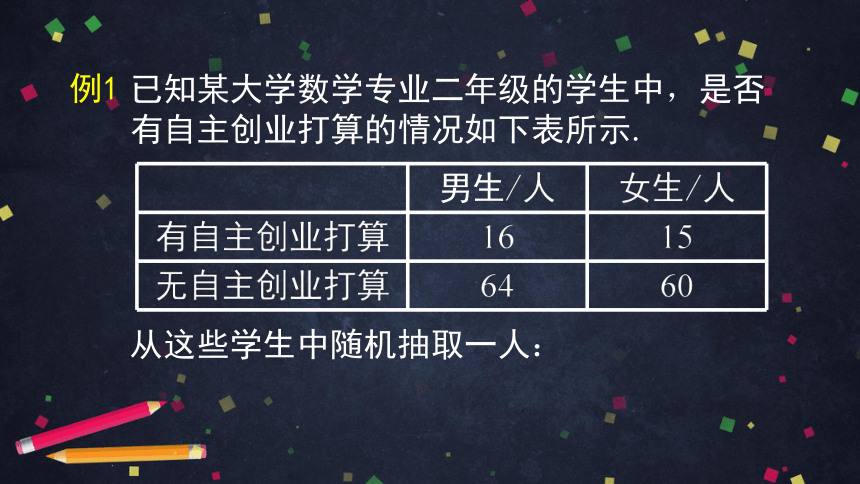
已知某大学数学专业二年级的学生中,是否有自主创业打算的情况如下表所示.
男生/人 女生/人
有自主创业打算 16 15
无自主创业打算 64 60
从这些学生中随机抽取一人:
解:
记为“抽到的人有自主创业打算”.
由题意可知,所有学生人数为,有自主创业打算的人数为.
所以抽到的人有自主创业打算的
概率为.
(1)求抽到的人有自主创业打算的概率;
例1
例1
(2)求抽到的人是女生的概率;
解:
记为“抽到的人是女生”.
由题意可知,所有学生人数为,女生人数为
所以抽到的人是女生的概率为.
例1
(3)若已知抽到的人是女生,求她有自主创业打算的概率;
解:
所要求的是,注意到75名女生中有15人有自主创业打算,因此.
(也可利用条件概率公式)
(4)判断“抽到的是女生”与“抽到的人有自主创业打算”是否独立.
例1
男生/人 女生/人
有自主创业打算 16 15
无自主创业打算 64 60
分析:
可以借助来判断与是否独立.
(4)判断“抽到的是女生”与“抽到的人有自主创业打算”是否独立.
例1
解:
由(1)和(3)的计算结果可知,因此“抽到的人是女生”与“抽到的人有自主创业打算”独立.
(4)判断“抽到的是女生”与“抽到的人有自主创业打算”是否独立.
例1
拓展:
有自主创业打算的女生人数由原来的15人改为16人,判断“抽到的人是女生”与“抽到的人有自主创业打算”是否独立.
解:
可知,则“抽到的人是女生”与“抽到的人有自主创业打算”不独立.
小结:
判断与独立的依据:
例2
已知甲、乙、丙3人参加驾照考试时,通过的概率分别为0.8,0.9,0.7,而且这3人之间的考试互不影响.求:
(1)甲、乙、丙都通过的概率;
(2)甲、乙通过且丙未通过的概率.
分析:
用,,分别表示甲、乙、丙驾照考试通过,则可知,,独立,而且,,.
已知多个事件,,…,相互独立,求这些事件同时发生的概率,可以利用计算.
解:
(1)甲、乙、丙都通过可用表示,因此所求概率为
解:
(2)甲、乙通过且丙未通过可用表示,因此所求概率为
拓展:
甲、乙、丙至少有一位通过考试的概率是多少?
分析:
由于,,三个事件不是互斥事件,因此不能利用求解,但可以借助对立事件和事件的独立性进行转化.
的对立事件为.
所求事件可以
解:
甲、乙、丙都通过可用表示,因此所求概率为
小结:
独立乘法公式的灵活应用
借助间接法求对立事件的概率
例3
在一个系统中,每个部件能正常工作的概率称为部件的可靠度,而系统能正常工作的概率称为系统的可靠度.现有甲、乙、丙3个部件组成的一个如图所示的系统,已知当甲正常工作且乙、丙至少有一个能正常工作时,系统就能正常工作,各部件的可靠度均为,而且甲、乙、丙互不影响.求系统的可靠度.
分析:
该问题可类比成一个带开关的电路,甲、乙丙相当于3个开关.
电路连通需要甲开关闭合,且乙开关或丙开关至少有一个闭合.
用,,表示甲、乙、丙能正常工作,表示系统能正常工作.
由题意知,系统能正常工作时,可分为三种互斥的情况:
分析:
甲、丙正常工作,且乙不正常工作,即;
甲、乙、丙都正常工作,即;
甲、乙正常工作,且丙不正常工作,即.
因此.
因为甲、乙、丙互不影响,所以,,相互独立,而且.
由互斥事件概率的加法公式以及独立性求解.
用,,表示甲、乙、丙能正常工作,表示系统能正常工作,则
解:
课堂小结
1.探究了事件独立性与条件概率的关系.
2.学习了事件独立性充要条件并灵活解决问题.
3.运用化归转化思想,将复杂问题分解,并用数学语言来表述实际问题.
作业
1.已知,,判断与是否独立.
2.已知与独立,且,,求.
3.加工某一零件需经过三道工序,设第一、二、三道工序的次品率分别为,,,且各道工序互不影响,求加工出来的零件的次品率.
谢谢
独立性与条件概率的关系
高二年级 数学
知识回顾:
1.条件概率的概念和计算公式是什么?
一般地,当事件发生的概率大于0时(即),已知事件发生的条件下事件发生的概率,称为条件概率,记作.
知识回顾:
2.事件与事件相互独立的充要条件是什么?
知识回顾:
3.事件与事件独立的直观理解是什么?
事件是否发生不会影响事件发生的概率,事件是否发生也不会影响事件发生的概率.
思考:
事件与事件独立的直观理解的数学含义是什么?
尝试与探究:
假设且,在与独立的前提下,通过条件概率的计算公式考察与的关系,以及与的关系.
分析:
当且时,由条件概率的计算公式有
分析:
类似地,可以看出,如果,那么一定有
.
事件独立的充要条件:
当时,与独立的充要条件是:
例1
已知某大学数学专业二年级的学生中,是否有自主创业打算的情况如下表所示.
男生/人 女生/人
有自主创业打算 16 15
无自主创业打算 64 60
从这些学生中随机抽取一人:
解:
记为“抽到的人有自主创业打算”.
由题意可知,所有学生人数为,有自主创业打算的人数为.
所以抽到的人有自主创业打算的
概率为.
(1)求抽到的人有自主创业打算的概率;
例1
例1
(2)求抽到的人是女生的概率;
解:
记为“抽到的人是女生”.
由题意可知,所有学生人数为,女生人数为
所以抽到的人是女生的概率为.
例1
(3)若已知抽到的人是女生,求她有自主创业打算的概率;
解:
所要求的是,注意到75名女生中有15人有自主创业打算,因此.
(也可利用条件概率公式)
(4)判断“抽到的是女生”与“抽到的人有自主创业打算”是否独立.
例1
男生/人 女生/人
有自主创业打算 16 15
无自主创业打算 64 60
分析:
可以借助来判断与是否独立.
(4)判断“抽到的是女生”与“抽到的人有自主创业打算”是否独立.
例1
解:
由(1)和(3)的计算结果可知,因此“抽到的人是女生”与“抽到的人有自主创业打算”独立.
(4)判断“抽到的是女生”与“抽到的人有自主创业打算”是否独立.
例1
拓展:
有自主创业打算的女生人数由原来的15人改为16人,判断“抽到的人是女生”与“抽到的人有自主创业打算”是否独立.
解:
可知,则“抽到的人是女生”与“抽到的人有自主创业打算”不独立.
小结:
判断与独立的依据:
例2
已知甲、乙、丙3人参加驾照考试时,通过的概率分别为0.8,0.9,0.7,而且这3人之间的考试互不影响.求:
(1)甲、乙、丙都通过的概率;
(2)甲、乙通过且丙未通过的概率.
分析:
用,,分别表示甲、乙、丙驾照考试通过,则可知,,独立,而且,,.
已知多个事件,,…,相互独立,求这些事件同时发生的概率,可以利用计算.
解:
(1)甲、乙、丙都通过可用表示,因此所求概率为
解:
(2)甲、乙通过且丙未通过可用表示,因此所求概率为
拓展:
甲、乙、丙至少有一位通过考试的概率是多少?
分析:
由于,,三个事件不是互斥事件,因此不能利用求解,但可以借助对立事件和事件的独立性进行转化.
的对立事件为.
所求事件可以
解:
甲、乙、丙都通过可用表示,因此所求概率为
小结:
独立乘法公式的灵活应用
借助间接法求对立事件的概率
例3
在一个系统中,每个部件能正常工作的概率称为部件的可靠度,而系统能正常工作的概率称为系统的可靠度.现有甲、乙、丙3个部件组成的一个如图所示的系统,已知当甲正常工作且乙、丙至少有一个能正常工作时,系统就能正常工作,各部件的可靠度均为,而且甲、乙、丙互不影响.求系统的可靠度.
分析:
该问题可类比成一个带开关的电路,甲、乙丙相当于3个开关.
电路连通需要甲开关闭合,且乙开关或丙开关至少有一个闭合.
用,,表示甲、乙、丙能正常工作,表示系统能正常工作.
由题意知,系统能正常工作时,可分为三种互斥的情况:
分析:
甲、丙正常工作,且乙不正常工作,即;
甲、乙、丙都正常工作,即;
甲、乙正常工作,且丙不正常工作,即.
因此.
因为甲、乙、丙互不影响,所以,,相互独立,而且.
由互斥事件概率的加法公式以及独立性求解.
用,,表示甲、乙、丙能正常工作,表示系统能正常工作,则
解:
课堂小结
1.探究了事件独立性与条件概率的关系.
2.学习了事件独立性充要条件并灵活解决问题.
3.运用化归转化思想,将复杂问题分解,并用数学语言来表述实际问题.
作业
1.已知,,判断与是否独立.
2.已知与独立,且,,求.
3.加工某一零件需经过三道工序,设第一、二、三道工序的次品率分别为,,,且各道工序互不影响,求加工出来的零件的次品率.
谢谢
