2023--2024学年湘教版数学九年级上册:1.2反比例函数的图像与性质(第2课时) 课件 24张PPT
文档属性
| 名称 | 2023--2024学年湘教版数学九年级上册:1.2反比例函数的图像与性质(第2课时) 课件 24张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-31 00:00:00 | ||
图片预览








文档简介
1.2 反比例函数的
图象与性质
第2课时 反比例函数y = ???????? (k < 0)
的图象与性质
?
1.了解反比例函数 的相关性质.
(重点、难点)
2.理解双曲线的概念以及其与反比例函数的联系.
(重点、难点)
3.利用双曲线的性质解决简单的数学问题.
学习目标
探 究
如何画反比例函数 y=-6x 的图象? y=-6x 的图像与y= 6x 的图像有什么关系?
?
当x=3时,y=-6x 的函数值为-2,而 y = 6x
的函数值为2.
在平面直角坐标系内,点A(3,-2)与B(3,2)关
于x轴对称,如图所示.
?
类似地,当x取任一非零实数a时, y=-6x 的函数值为-6???? ,
而 y= 6x?的函数值为 6???? ,
从而都有点P(a,?6a)与点Q (a,6a) 关于x轴对称,
因此 y=-6x?的图象与 y= 6x 的图象关于x轴对称.
于是只要把 y= 6x 的图象沿着x轴翻折并将图象“复制”出来,
就得到了 y=-6x?的图象,如图中的红色曲线所示.
?
O
5
6
x
4
3
2
1
1
2
3
4
5
6
-1
-1
-2
-3
-4
-5
-6
-2
-3
-4
-5
-6
从图看出: y=-6x 的图象由分别在第二、四象限的两支曲线组成.
它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量x的增大而增大.
?
类似地,当 k < 0 时,反比例函数 y = ????x 的图象与 y=-????x 的图象关于 x 轴对称,
从而当 k < 0 时,反比例函数 y =-????x 的图象由分别在第二、四象限内的两支曲线组成,它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量 x 的增大而增大 .
?
例1:画反比例函数 的图象.
解析:通过上节课学习可知画图象的三个步骤为:
列表
描点
连线
需要注意的是在反比例函数中自变量x不能为0.
解:列表如下
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
y
…
23
0.8
1
43
2
4
-4
-2
?43
-1
-0.8
?23
…
典例精析
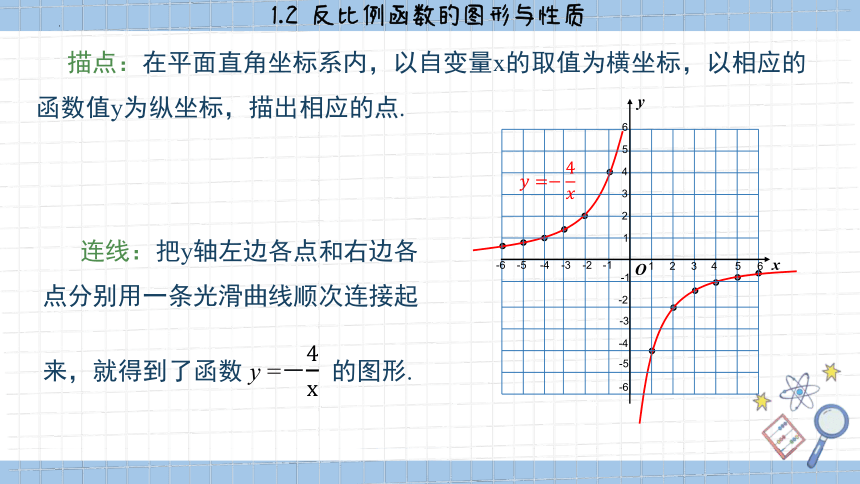
描点:在平面直角坐标系内,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点.
{BC89EF96-8CEA-46FF-86C4-4CE0E7609802}
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
y
x
O
????=?4????
?
连线:把y轴左边各点和右边各点分别用一条光滑曲线顺次连接起来,就得到了函数 y =-4x?的图形.
?
综上所述,我们得到:
反比例函数 y =-4x?(k为常数,k≠0)的图象是由两支曲线组成的,这两支曲线称为双曲线.
?
y =-????x?(k < 0)图象的画法与y =-????x?(k > 0)图象的画法类似,但在解题的时候要注意图象所在的象限.
?
(1) 当 k > 0 时,双曲线的两支分别位于第一、三
象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四
象限,在每一象限内,y 随 x 的增大而增大.
一般地,反比例函数 y = ???????? 的图象是双曲线,它具有以下性质:
?
k 的正负决定反比例函数所在的象限和增减性
总结归纳
问题:观察前面绘制出来的图象,想一想它们有什么样的共同点与特征呢?
x
y
x
y
双曲线
O
O
二、双曲线的概念及性质
是轴对称图形,也是
以原点为对称中心的中心对称图形.
1、如图,已知直线y=mx与双曲线 的一个交点坐标为(-1,3),则它们的另一个交点坐标是( )
A. (1,3) B. (3,1)
C. (1,-3) D. (-1,3)
x
y
C
O
练 一 练
2、点(2,y1)和(3,y2)在函数 上,则 y1 y2.(填“>”“<”或“=”)
<
解析:由题意知该反比例函数位于第二、四象限,且y随着自变量x的增大而增大,故y1练 习
1.画出下列反比例函数的图象:
(1)?????=?3???? ;
?
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}x
-3
-2
?32
-1
1
32
2
y
1
32
2
3
-3
-2
?32
(1)列表
作图:
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}x
-2
-1
?14
14
1
2
y
14
12
2
-2
?12
?14
(2)列表
作图:
(2)y = -12????
?
3. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
2. 已知反比例函数 的图象在第一、三象限内,则m的取值范围是________.
m > 2
4.已知反比例函数的图象的一支如图所示.
(1)判断k是正数还是负数;
(2)求这个反比例函数的表达式;
(3)补画这个反比例函数图象的另一支.
解:(1)因为反比例函数的图象在第二象限,所以k是负数.
(2)设反比例函数的表达式为 将(-4,2)代入其中,解得k=-8,所以反比例函数的表达式为:
(3)根据反比例函数图象的中心对称性可补画出另一支,图象略.
5. 已知反比例函数 的图象经过点 A (2,-4).
(1) 求 k 的值;
(2) 这个函数的图象分布在哪些象限?y 随 x 的增大如何变化?
解:(1)∵ 反比例函数 y = ???????? 的图象经过点 A(2,-4),
∴ 把点 A 的坐标代入表达式,得 -4 = ????2 ,
解得 k = -8.
?
(2) y = ?8???? 这个函数的图象位于第二、四象限,在每一个
象限内,y 随 x 的增大而增大.
?
(3) 画出该函数的图象;
O
x
y
解:如图所示:
(3) 点 B (1,-8) ,C (-3,5)是否在该函数的图象上?
解:把 x =1代入反比例函数解析式 y =- 81=-8 ,
把 x = -3代入反比例函数解析式 y= - 8?3?= 83?≠ 5,
所以点B(1,-8)不在这个函数的图象上,
点C(-3,5)在这个函数的图象上.
?
能力提升:
7. 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)
的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
① 当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1.
反比例函数 (k≠0)
k
k > 0
k < 0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随
x 的增大而增大
课堂小结
本课结束
图象与性质
第2课时 反比例函数y = ???????? (k < 0)
的图象与性质
?
1.了解反比例函数 的相关性质.
(重点、难点)
2.理解双曲线的概念以及其与反比例函数的联系.
(重点、难点)
3.利用双曲线的性质解决简单的数学问题.
学习目标
探 究
如何画反比例函数 y=-6x 的图象? y=-6x 的图像与y= 6x 的图像有什么关系?
?
当x=3时,y=-6x 的函数值为-2,而 y = 6x
的函数值为2.
在平面直角坐标系内,点A(3,-2)与B(3,2)关
于x轴对称,如图所示.
?
类似地,当x取任一非零实数a时, y=-6x 的函数值为-6???? ,
而 y= 6x?的函数值为 6???? ,
从而都有点P(a,?6a)与点Q (a,6a) 关于x轴对称,
因此 y=-6x?的图象与 y= 6x 的图象关于x轴对称.
于是只要把 y= 6x 的图象沿着x轴翻折并将图象“复制”出来,
就得到了 y=-6x?的图象,如图中的红色曲线所示.
?
O
5
6
x
4
3
2
1
1
2
3
4
5
6
-1
-1
-2
-3
-4
-5
-6
-2
-3
-4
-5
-6
从图看出: y=-6x 的图象由分别在第二、四象限的两支曲线组成.
它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量x的增大而增大.
?
类似地,当 k < 0 时,反比例函数 y = ????x 的图象与 y=-????x 的图象关于 x 轴对称,
从而当 k < 0 时,反比例函数 y =-????x 的图象由分别在第二、四象限内的两支曲线组成,它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量 x 的增大而增大 .
?
例1:画反比例函数 的图象.
解析:通过上节课学习可知画图象的三个步骤为:
列表
描点
连线
需要注意的是在反比例函数中自变量x不能为0.
解:列表如下
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
y
…
23
0.8
1
43
2
4
-4
-2
?43
-1
-0.8
?23
…
典例精析
描点:在平面直角坐标系内,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点.
{BC89EF96-8CEA-46FF-86C4-4CE0E7609802}
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
-6
-5
5
6
y
x
O
????=?4????
?
连线:把y轴左边各点和右边各点分别用一条光滑曲线顺次连接起来,就得到了函数 y =-4x?的图形.
?
综上所述,我们得到:
反比例函数 y =-4x?(k为常数,k≠0)的图象是由两支曲线组成的,这两支曲线称为双曲线.
?
y =-????x?(k < 0)图象的画法与y =-????x?(k > 0)图象的画法类似,但在解题的时候要注意图象所在的象限.
?
(1) 当 k > 0 时,双曲线的两支分别位于第一、三
象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四
象限,在每一象限内,y 随 x 的增大而增大.
一般地,反比例函数 y = ???????? 的图象是双曲线,它具有以下性质:
?
k 的正负决定反比例函数所在的象限和增减性
总结归纳
问题:观察前面绘制出来的图象,想一想它们有什么样的共同点与特征呢?
x
y
x
y
双曲线
O
O
二、双曲线的概念及性质
是轴对称图形,也是
以原点为对称中心的中心对称图形.
1、如图,已知直线y=mx与双曲线 的一个交点坐标为(-1,3),则它们的另一个交点坐标是( )
A. (1,3) B. (3,1)
C. (1,-3) D. (-1,3)
x
y
C
O
练 一 练
2、点(2,y1)和(3,y2)在函数 上,则 y1 y2.(填“>”“<”或“=”)
<
解析:由题意知该反比例函数位于第二、四象限,且y随着自变量x的增大而增大,故y1
1.画出下列反比例函数的图象:
(1)?????=?3???? ;
?
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}x
-3
-2
?32
-1
1
32
2
y
1
32
2
3
-3
-2
?32
(1)列表
作图:
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}x
-2
-1
?14
14
1
2
y
14
12
2
-2
?12
?14
(2)列表
作图:
(2)y = -12????
?
3. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
2. 已知反比例函数 的图象在第一、三象限内,则m的取值范围是________.
m > 2
4.已知反比例函数的图象的一支如图所示.
(1)判断k是正数还是负数;
(2)求这个反比例函数的表达式;
(3)补画这个反比例函数图象的另一支.
解:(1)因为反比例函数的图象在第二象限,所以k是负数.
(2)设反比例函数的表达式为 将(-4,2)代入其中,解得k=-8,所以反比例函数的表达式为:
(3)根据反比例函数图象的中心对称性可补画出另一支,图象略.
5. 已知反比例函数 的图象经过点 A (2,-4).
(1) 求 k 的值;
(2) 这个函数的图象分布在哪些象限?y 随 x 的增大如何变化?
解:(1)∵ 反比例函数 y = ???????? 的图象经过点 A(2,-4),
∴ 把点 A 的坐标代入表达式,得 -4 = ????2 ,
解得 k = -8.
?
(2) y = ?8???? 这个函数的图象位于第二、四象限,在每一个
象限内,y 随 x 的增大而增大.
?
(3) 画出该函数的图象;
O
x
y
解:如图所示:
(3) 点 B (1,-8) ,C (-3,5)是否在该函数的图象上?
解:把 x =1代入反比例函数解析式 y =- 81=-8 ,
把 x = -3代入反比例函数解析式 y= - 8?3?= 83?≠ 5,
所以点B(1,-8)不在这个函数的图象上,
点C(-3,5)在这个函数的图象上.
?
能力提升:
7. 点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)
的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
① 当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1.
反比例函数 (k≠0)
k
k > 0
k < 0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随
x 的增大而增大
课堂小结
本课结束
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
