2023-2024学年初中湘教版数学九年级上册第2章 一元二次方程:2.4一元二次方程根与系数的关系课件 21张PPT
文档属性
| 名称 | 2023-2024学年初中湘教版数学九年级上册第2章 一元二次方程:2.4一元二次方程根与系数的关系课件 21张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 43.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-31 07:53:30 | ||
图片预览








文档简介
(共21张PPT)
2.4 一元二次方程根与系数的关系
学习目标
1.探索一元二次方程的根与系数的关系.(难点)
2.不解方程利用一元二次方程的根与系数的关系解决问题.(重点)
1.一元二次方程的求根公式是什么?
想一想:方程的两根x1和x2与系数a,b,c还有其它关系吗?
2.如何用判别式 b2 - 4ac 来判断一元二次方程根的情况?
对一元二次方程: ax2 + bx +c = 0(a ≠ 0)
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
复习引入
一、探索一元二次方程的根与系数的关系
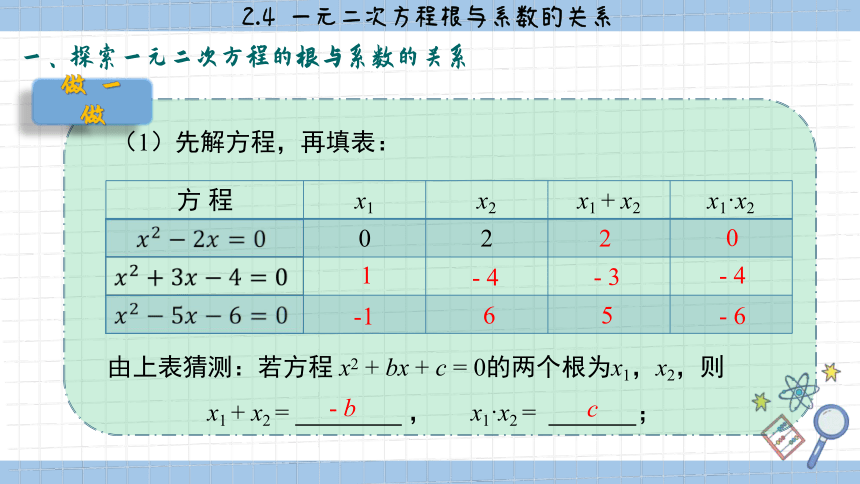
做 一 做
(1)先解方程,再填表:
方 程 x1 x2 x1 + x2 x1·x2
0 2
由上表猜测:若方程 x2 + bx + c = 0的两个根为x1,x2,则
x1 + x2 = , x1·x2 = ;
2
0
- 4
- 3
- 4
1
-1
6
5
- 6
- b
c
做 一 做
(2)方程 x2 - 5x + 6 = 0的两个根为 x1 = ,x2 = ,
根据2.2节例8下面的一段话,得 x2 - 5x + 6 = (x - )(x - ).
若我们能把方程 x2 + bx + c = 0的左边进行因式分解后,写成
x2 + bx + c = (x - d)(x - h) = 0,
则 d 和 h 就是方程 x2 + bx + c = 0的根.
反过来,如果 d 和 h 是方程 x2 + bx + c = 0的根,则方程的左边就可以分解成
x2 + bx + c = (x - d)(x - h).
2
3
2
3
动 脑 筋
对于方程 ax2 + bx + c = 0(a ≠ 0),当 Δ ≥ 0 时,该方程的根与它的系数之间有什么关系呢?
当Δ ≥ 0时,设ax2 + bx + c = 0(a ≠ 0)的两个根为x1,x2,则
ax2 + bx + c = a(x - x1)(x - x2)
= a[x2 - (x1 + x2)x + x1x2],
根据七年级上册教科书2.5节关于两个多项式相等的规定,得
即
这个关系通常被称为韦达定理.
两根的和等于一次项系数与二次项系数的比的相反数,
这表明,当 Δ ≥ 0 时,一元二次方程的根与系数之间具有如下关系:
归纳总结
两根的积等于常数项与二次项系数的比.
解:这里 a = 2 , b = -3 , c = 1.
Δ = b2 - 4ac = (- 3)2 – 4×2×1 = 1 > 0,
∴方程有两个实数根.
那么 x1 + x2 = , x1 x2 = .
二、一元二次方程的根与系数的关系的应用
例1 根据一元二次方程根与系数的关系,求下列方程的两根 x1,x2的和与积:
(2)x2 - 3x + 2 =10.
解:(2)整理,得 x2 - 3x - 8 = 0,
这里 a = 1 , b = -3 , c = -8.
Δ = b2 - 4ac
= (- 3)2 – 4 × 1 × (-8)
= 41 > 0,
∴方程有两个实数根.
那么 x1 + x2 = 3 ,x1 x2 = -8 .
(3)7x2 – 5 = x + 8.
(3)整理,得7x2 – x – 13 = 0,
这里 a = 7 ,b = -1 , c = -13.
Δ = b2 - 4ac
= (- 1)2 – 4 × 7 ×(-13)
= 365 > 0,
∴方程有两个实数根.
那么 x1 + x2 = ,x1 x2 = - .
解:设方程的两个根分别是 x1、x2,其中 x1 = -3 .
则:x1 + x2 = (-3) + x2 = -3,
解得 x2 = 0
由根与系数之间的关系得
x1·x2 = q = (-3) × 0 = 0
得 q = 0.
答:方程的另一个根是 0,q = 0.
例2 已知方程 x2 + 3x + q = 0 的一个根是-3,求它的另一个根及 q 的值.
还可用其他方法求出 q 的值吗?
变式:已知方程 3x2 - 18x + m = 0 的一个根是1,求它的另一个根及 m 的值.
解:设方程的两个根分别是x1、x2,其中 x1 = 1.
所以:x1 + x2 = 1 + x2 = 6,
即:x2 = 5 .
由于 x1·x2 = 1×5 = ,
得:m =15.
答:方程的另一个根是5,m = 15.
不解方程,求方程 2x2 + 3x – 1 = 0 的两根的平方和、倒数和.
解:根据根与系数的关系可知:
练一练
2
1.根据一元二次方程根与系数的关系,求下列方程的两根的和与积:
(1) x2 - 6x + 1 = 0; (2) 2x2 – x = 6.
练 习
2.已知方程 3x2 - 19x + m = 0 的一个根为1,求它的另一个根及m的值.
解:由一元二次方程根与系数的关系,得
3.已知方程 3x2 -19x + m = 0 的一个根是1,求它的另一个根及 m 的值.
4.已知x1,x2是方程 2x2 + 2kx + k - 1 = 0的两个根,且(x1 + 1)(x2 + 1) = 4;
(1)求k的值; (2)求(x1-x2)2的值.
解:根据根与系数的关系得:
6. 当 k 为何值时,方程 2x2 – kx + 1 = 0的两根差为1.
解:设方程两根分别为 x1,x2(x1 > x2),则 x1 - x2 = 1
∵ (x1 - x2)2 = (x1 + x2)2 - 4x1x2 = 1
由根与系数的关系,得
拓展提升
7.已知关于x的一元二次方程 mx2-2mx+ m -2 = 0
(1)若方程有实数根,求实数m的取值范围.
(2)若方程两根x1,x2满足∣x1-x2∣= 1 求m的值.
解:(1)方程有实数根
∴m的取值范围为m>0
(2) ∵方程有实数根x1,x2
∵ (x1 - x2)2 = (x1 + x2)2 - 4x1x2 = 1
解得 m = 8.
经检验 m = 8是原方程的解.
本课结束
2.4 一元二次方程根与系数的关系
学习目标
1.探索一元二次方程的根与系数的关系.(难点)
2.不解方程利用一元二次方程的根与系数的关系解决问题.(重点)
1.一元二次方程的求根公式是什么?
想一想:方程的两根x1和x2与系数a,b,c还有其它关系吗?
2.如何用判别式 b2 - 4ac 来判断一元二次方程根的情况?
对一元二次方程: ax2 + bx +c = 0(a ≠ 0)
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
复习引入
一、探索一元二次方程的根与系数的关系
做 一 做
(1)先解方程,再填表:
方 程 x1 x2 x1 + x2 x1·x2
0 2
由上表猜测:若方程 x2 + bx + c = 0的两个根为x1,x2,则
x1 + x2 = , x1·x2 = ;
2
0
- 4
- 3
- 4
1
-1
6
5
- 6
- b
c
做 一 做
(2)方程 x2 - 5x + 6 = 0的两个根为 x1 = ,x2 = ,
根据2.2节例8下面的一段话,得 x2 - 5x + 6 = (x - )(x - ).
若我们能把方程 x2 + bx + c = 0的左边进行因式分解后,写成
x2 + bx + c = (x - d)(x - h) = 0,
则 d 和 h 就是方程 x2 + bx + c = 0的根.
反过来,如果 d 和 h 是方程 x2 + bx + c = 0的根,则方程的左边就可以分解成
x2 + bx + c = (x - d)(x - h).
2
3
2
3
动 脑 筋
对于方程 ax2 + bx + c = 0(a ≠ 0),当 Δ ≥ 0 时,该方程的根与它的系数之间有什么关系呢?
当Δ ≥ 0时,设ax2 + bx + c = 0(a ≠ 0)的两个根为x1,x2,则
ax2 + bx + c = a(x - x1)(x - x2)
= a[x2 - (x1 + x2)x + x1x2],
根据七年级上册教科书2.5节关于两个多项式相等的规定,得
即
这个关系通常被称为韦达定理.
两根的和等于一次项系数与二次项系数的比的相反数,
这表明,当 Δ ≥ 0 时,一元二次方程的根与系数之间具有如下关系:
归纳总结
两根的积等于常数项与二次项系数的比.
解:这里 a = 2 , b = -3 , c = 1.
Δ = b2 - 4ac = (- 3)2 – 4×2×1 = 1 > 0,
∴方程有两个实数根.
那么 x1 + x2 = , x1 x2 = .
二、一元二次方程的根与系数的关系的应用
例1 根据一元二次方程根与系数的关系,求下列方程的两根 x1,x2的和与积:
(2)x2 - 3x + 2 =10.
解:(2)整理,得 x2 - 3x - 8 = 0,
这里 a = 1 , b = -3 , c = -8.
Δ = b2 - 4ac
= (- 3)2 – 4 × 1 × (-8)
= 41 > 0,
∴方程有两个实数根.
那么 x1 + x2 = 3 ,x1 x2 = -8 .
(3)7x2 – 5 = x + 8.
(3)整理,得7x2 – x – 13 = 0,
这里 a = 7 ,b = -1 , c = -13.
Δ = b2 - 4ac
= (- 1)2 – 4 × 7 ×(-13)
= 365 > 0,
∴方程有两个实数根.
那么 x1 + x2 = ,x1 x2 = - .
解:设方程的两个根分别是 x1、x2,其中 x1 = -3 .
则:x1 + x2 = (-3) + x2 = -3,
解得 x2 = 0
由根与系数之间的关系得
x1·x2 = q = (-3) × 0 = 0
得 q = 0.
答:方程的另一个根是 0,q = 0.
例2 已知方程 x2 + 3x + q = 0 的一个根是-3,求它的另一个根及 q 的值.
还可用其他方法求出 q 的值吗?
变式:已知方程 3x2 - 18x + m = 0 的一个根是1,求它的另一个根及 m 的值.
解:设方程的两个根分别是x1、x2,其中 x1 = 1.
所以:x1 + x2 = 1 + x2 = 6,
即:x2 = 5 .
由于 x1·x2 = 1×5 = ,
得:m =15.
答:方程的另一个根是5,m = 15.
不解方程,求方程 2x2 + 3x – 1 = 0 的两根的平方和、倒数和.
解:根据根与系数的关系可知:
练一练
2
1.根据一元二次方程根与系数的关系,求下列方程的两根的和与积:
(1) x2 - 6x + 1 = 0; (2) 2x2 – x = 6.
练 习
2.已知方程 3x2 - 19x + m = 0 的一个根为1,求它的另一个根及m的值.
解:由一元二次方程根与系数的关系,得
3.已知方程 3x2 -19x + m = 0 的一个根是1,求它的另一个根及 m 的值.
4.已知x1,x2是方程 2x2 + 2kx + k - 1 = 0的两个根,且(x1 + 1)(x2 + 1) = 4;
(1)求k的值; (2)求(x1-x2)2的值.
解:根据根与系数的关系得:
6. 当 k 为何值时,方程 2x2 – kx + 1 = 0的两根差为1.
解:设方程两根分别为 x1,x2(x1 > x2),则 x1 - x2 = 1
∵ (x1 - x2)2 = (x1 + x2)2 - 4x1x2 = 1
由根与系数的关系,得
拓展提升
7.已知关于x的一元二次方程 mx2-2mx+ m -2 = 0
(1)若方程有实数根,求实数m的取值范围.
(2)若方程两根x1,x2满足∣x1-x2∣= 1 求m的值.
解:(1)方程有实数根
∴m的取值范围为m>0
(2) ∵方程有实数根x1,x2
∵ (x1 - x2)2 = (x1 + x2)2 - 4x1x2 = 1
解得 m = 8.
经检验 m = 8是原方程的解.
本课结束
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
