矩形2[下学期]
图片预览






文档简介
课件22张PPT。矩形的判定石塘镇中学 林小丹给你一根足够长的绳子,你能用这根绳子来检查数学课本是否是矩形吗? 1、想一想:矩形是如何定义的?矩形具有哪些性质?哪些是平行四边形所没有的?列表比较:对边平行且相等 对边平行且相等 对角相等 四个角都是直角 互相平分且相等 互相平分 2.目前我们判定一个四边形是矩形,只能依据什么?3.还有其他方法来判定吗?矩形的定义:有一个角是直角的平行四边形是矩形
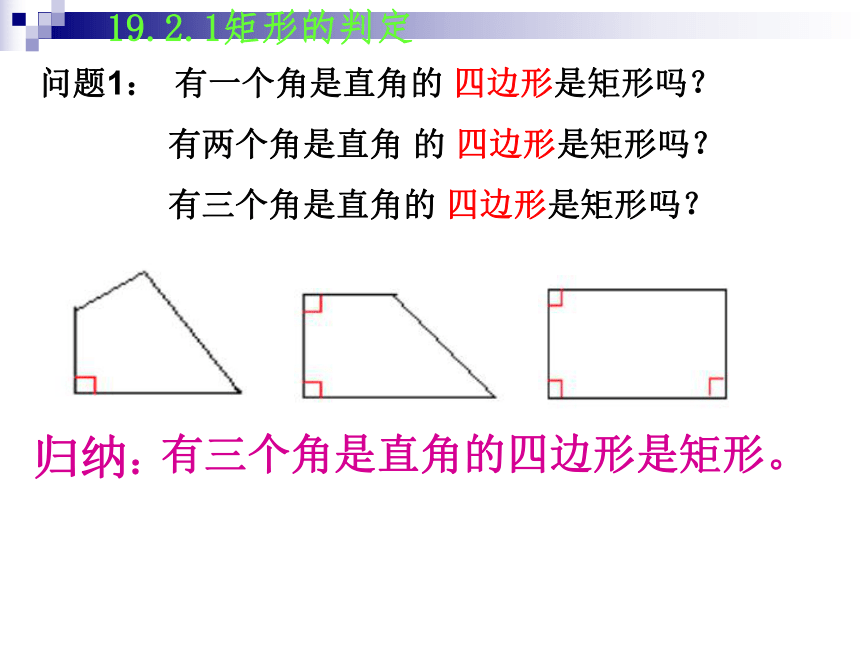
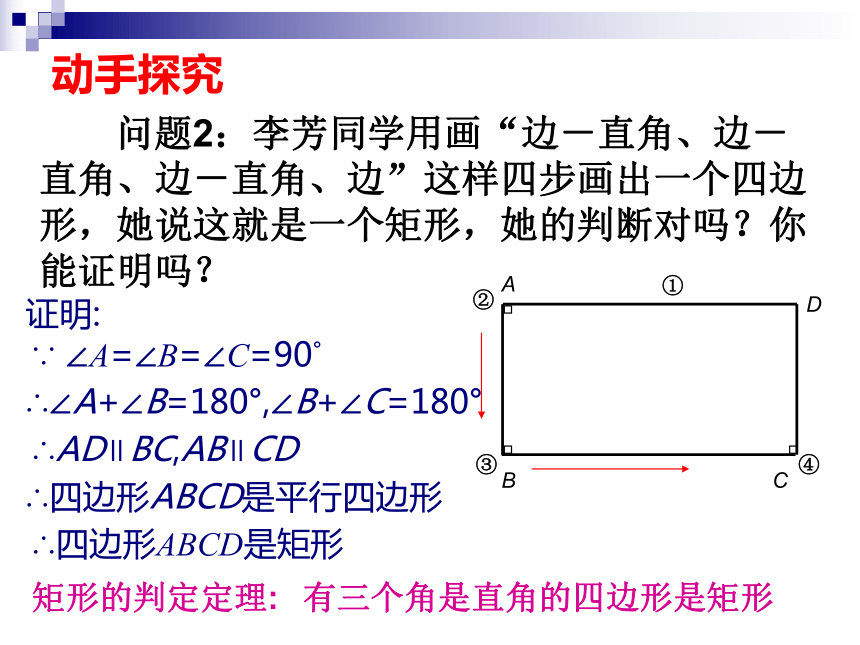
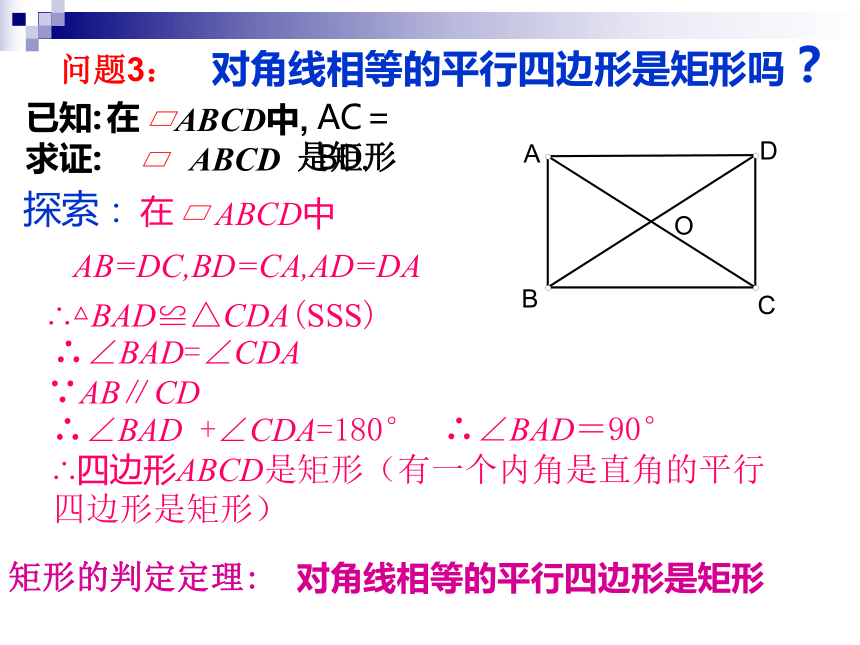
归纳:有三个角是直角的四边形是矩形。19.2.1矩形的判定有一个角是直角的 四边形是矩形吗?有两个角是直角 的 四边形是矩形吗?有三个角是直角的 四边形是矩形吗?问题1:动手探究 问题2:李芳同学用画“边-直角、边-直角、边-直角、边”这样四步画出一个四边形,她说这就是一个矩形,她的判断对吗?你能证明吗?②①③④ABCD证明:∵ ∠A=∠B=∠C=90°∴四边形ABCD是平行四边形∴四边形ABCD是矩形∴∠A+∠B=180°,∠B+∠C=180°∴AD∥BC,AB∥CD矩形的判定定理:有三个角是直角的四边形是矩形对角线相等的平行四边形是矩形探索:AB=DC,BD=CA,AD=DA∴△BAD≌△CDA(SSS)∴∠BAD=∠CDA∵AB∥CD∴∠BAD +∠CDA=180° ∴∠BAD=90° ∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形)对角线相等的平行四边形是矩形吗?问题3:已知:AC=BD.求证:是矩形矩形的判定定理:(1)三个角都是直角的四边形是矩形.有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.矩形的判定方法:1﹑矩形的定义:2﹑矩形的判定定理:1﹑议一议:判断下列说法是否正确,并说明理由。④对角线相等且互相垂直的四边形是矩形。
( 错 ) ( 对 ) ( 错 ) ( 错 ) ①对角线相等的四边形是矩形。…………..
②对角线互相平分且相等的四边形是矩形。③四个角都相等的四边形是矩形。………..2﹑四边形ABCD的对角线AC﹑BD相交于点O,能判断它是矩形的条件是 ( )A﹑AO=CO,BO=DO
B﹑AB=BC,AO=CO
C﹑AO=CO,BO=DO,AC⊥BD
D﹑AO=BO=CO=DOD已知:如图,AC与BD相交于点O,AB CD ,且∠1=∠2 。 求证:四边形ABCD是矩形例1证明:∵例2、BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,求证:四边形AEBD是矩形。例3、AC、BD是矩形ABCD的两条对角线,且AE=CG=BF=DH,求证:四边形EFGH是矩形。ABCDEFGHO(3)将直角尺紧靠窗框的一个角(如图3)调整窗框的边框,当直角尺的两直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框形状是____,根据的数学原理是___________.1﹑工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1)使AB=CD,EF=GH(2)摆放成如图2的四边形,则这时窗框的形状是____,根据的数学原理是_______ ;平行四边形两组对边分别相等的四边形是平行四边形矩形有一个角为直角的平行四边形是矩形生活应用2﹑工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否分别相等,还要测量它们的两条对角线是否相等,以确保图形是矩形,你知道其中的道理吗?生活应用答:测量对边长度相等,保证平行四边形。再测量对角线相等,保证它是矩形。3﹑给你一根足够长的绳子,你能用这根绳子来检查数学课本是否是矩形吗?说明方法并用数学知识来说明理由。生活应用 4﹑ 为庆祝五一劳动节,学校交给八(2)班同学一个任务:在广场上布置一个矩形的花坛(如图).同学们计划用“串红”摆成两条对角线.如果一条对角线用了38盆“串红”,这需要从花房搬来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?答:(1)需要再搬来38盆串红,根据矩形的对角线相等, 另外这时对角线交点处不放花;(2)需要再搬来48盆串红,根据矩形的对角线相等,另外这时对角线交点处要放花。生活应用1﹑如图,的对角线AC,BD关于点O,△ ABO是等边三角形,AB=4㎝,求的面积(精确到0.01㎝)知识拓展答:27.71㎝22﹑在平面直角坐标系中,四边形ABCD的四个顶点坐标分别是A(0,﹣1),B(4,﹣1),C(4,﹣6),D(0,﹣6),试画图说明四边形ABCD是怎样的四边形。你能根据四边形的顶点坐标来说明四边形的两条对角线的关系吗?知识拓展ABCD学习了本节课你有哪些收获?如图, 在平行四边形ABCD中,AF,BH,CH,DF分别
平分∠BAD, ∠ABC, ∠BCD, ∠ADC,
求证:EG=HF.ABCDHEFG挑战无处不在一张四边形的纸板ABCD的形状如图(1),
它的两条对角线AC,BD互相垂直。
如果要从这张纸板中剪出一个矩形,
并且使它的四个顶点分别落在四边形ABCD
的四条边上,可以怎么剪?
解:分别取AB,BC,CD,DA的中点E,F,G,H,依次连接EF,FG,GH,HE,沿四边形EFGH的各条边剪,就能剪出符合要求的矩形.证明如下:∵EF是△ABC的一条中位线
∴EF∥AC(三角形的中位线平行于第三边)
∵AC⊥BD ∴EF ⊥BD
∵EH是△ ABD的一条中位线
∴ EH ∥BD ∴EF ⊥EH 即∠HEF=Rt ∠
同理,∠EHG=Rt ∠ ,∠HGF=Rt ∠.
∴四边形EFGH是矩形(有三个角是直角的四边形是矩形)
归纳:有三个角是直角的四边形是矩形。19.2.1矩形的判定有一个角是直角的 四边形是矩形吗?有两个角是直角 的 四边形是矩形吗?有三个角是直角的 四边形是矩形吗?问题1:动手探究 问题2:李芳同学用画“边-直角、边-直角、边-直角、边”这样四步画出一个四边形,她说这就是一个矩形,她的判断对吗?你能证明吗?②①③④ABCD证明:∵ ∠A=∠B=∠C=90°∴四边形ABCD是平行四边形∴四边形ABCD是矩形∴∠A+∠B=180°,∠B+∠C=180°∴AD∥BC,AB∥CD矩形的判定定理:有三个角是直角的四边形是矩形对角线相等的平行四边形是矩形探索:AB=DC,BD=CA,AD=DA∴△BAD≌△CDA(SSS)∴∠BAD=∠CDA∵AB∥CD∴∠BAD +∠CDA=180° ∴∠BAD=90° ∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形)对角线相等的平行四边形是矩形吗?问题3:已知:AC=BD.求证:是矩形矩形的判定定理:(1)三个角都是直角的四边形是矩形.有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.矩形的判定方法:1﹑矩形的定义:2﹑矩形的判定定理:1﹑议一议:判断下列说法是否正确,并说明理由。④对角线相等且互相垂直的四边形是矩形。
( 错 ) ( 对 ) ( 错 ) ( 错 ) ①对角线相等的四边形是矩形。…………..
②对角线互相平分且相等的四边形是矩形。③四个角都相等的四边形是矩形。………..2﹑四边形ABCD的对角线AC﹑BD相交于点O,能判断它是矩形的条件是 ( )A﹑AO=CO,BO=DO
B﹑AB=BC,AO=CO
C﹑AO=CO,BO=DO,AC⊥BD
D﹑AO=BO=CO=DOD已知:如图,AC与BD相交于点O,AB CD ,且∠1=∠2 。 求证:四边形ABCD是矩形例1证明:∵例2、BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,求证:四边形AEBD是矩形。例3、AC、BD是矩形ABCD的两条对角线,且AE=CG=BF=DH,求证:四边形EFGH是矩形。ABCDEFGHO(3)将直角尺紧靠窗框的一个角(如图3)调整窗框的边框,当直角尺的两直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框形状是____,根据的数学原理是___________.1﹑工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1)使AB=CD,EF=GH(2)摆放成如图2的四边形,则这时窗框的形状是____,根据的数学原理是_______ ;平行四边形两组对边分别相等的四边形是平行四边形矩形有一个角为直角的平行四边形是矩形生活应用2﹑工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否分别相等,还要测量它们的两条对角线是否相等,以确保图形是矩形,你知道其中的道理吗?生活应用答:测量对边长度相等,保证平行四边形。再测量对角线相等,保证它是矩形。3﹑给你一根足够长的绳子,你能用这根绳子来检查数学课本是否是矩形吗?说明方法并用数学知识来说明理由。生活应用 4﹑ 为庆祝五一劳动节,学校交给八(2)班同学一个任务:在广场上布置一个矩形的花坛(如图).同学们计划用“串红”摆成两条对角线.如果一条对角线用了38盆“串红”,这需要从花房搬来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?答:(1)需要再搬来38盆串红,根据矩形的对角线相等, 另外这时对角线交点处不放花;(2)需要再搬来48盆串红,根据矩形的对角线相等,另外这时对角线交点处要放花。生活应用1﹑如图,的对角线AC,BD关于点O,△ ABO是等边三角形,AB=4㎝,求的面积(精确到0.01㎝)知识拓展答:27.71㎝22﹑在平面直角坐标系中,四边形ABCD的四个顶点坐标分别是A(0,﹣1),B(4,﹣1),C(4,﹣6),D(0,﹣6),试画图说明四边形ABCD是怎样的四边形。你能根据四边形的顶点坐标来说明四边形的两条对角线的关系吗?知识拓展ABCD学习了本节课你有哪些收获?如图, 在平行四边形ABCD中,AF,BH,CH,DF分别
平分∠BAD, ∠ABC, ∠BCD, ∠ADC,
求证:EG=HF.ABCDHEFG挑战无处不在一张四边形的纸板ABCD的形状如图(1),
它的两条对角线AC,BD互相垂直。
如果要从这张纸板中剪出一个矩形,
并且使它的四个顶点分别落在四边形ABCD
的四条边上,可以怎么剪?
解:分别取AB,BC,CD,DA的中点E,F,G,H,依次连接EF,FG,GH,HE,沿四边形EFGH的各条边剪,就能剪出符合要求的矩形.证明如下:∵EF是△ABC的一条中位线
∴EF∥AC(三角形的中位线平行于第三边)
∵AC⊥BD ∴EF ⊥BD
∵EH是△ ABD的一条中位线
∴ EH ∥BD ∴EF ⊥EH 即∠HEF=Rt ∠
同理,∠EHG=Rt ∠ ,∠HGF=Rt ∠.
∴四边形EFGH是矩形(有三个角是直角的四边形是矩形)
