初中几何证明的经典难题
图片预览
文档简介
初中几何证明的经典难题
一.割补法:
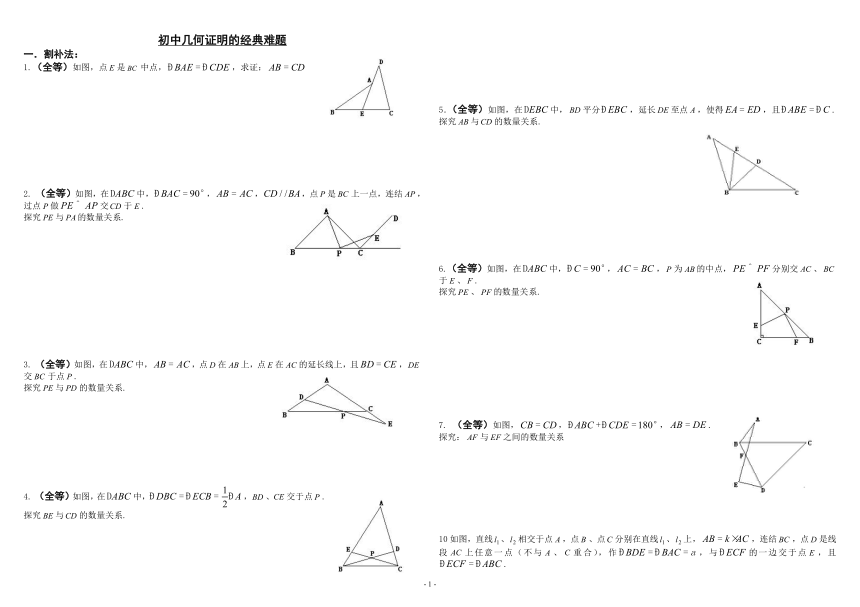
1.(全等)如图,点是中点,,求证:
2. (全等)如图,在中,,,,点是上一点,连结,过点做交于.
探究与的数量关系.
3. (全等)如图,在中,,点在上,点在的延长线上,且,交于点.
探究与的数量关系.
4. (全等)如图,在中,,、交于点.
探究与的数量关系.
5.(全等)如图,在中,平分,延长至点,使得,且.
探究与的数量关系.
6.(全等)如图,在中,,,为的中点,分别交、于、.
探究、的数量关系.
7. (全等)如图,,,.
探究:与之间的数量关系
10如图,直线、相交于点,点、点分别在直线、上,,连结,点是线段上任意一点(不与、重合),作,与的一边交于点,且.
⑴如图1,若,且时,猜想线段与的数量关系,并加以证明;
⑵如图2,若,时,猜想线段与的数量关系,并加以证明.
二.倍长中线法:
11. (全等)如图,点是中点,,求证:
13 (全等)如图,在中,,,是边的中线.求证:
15. (全等)如图,在中,平分,为的中点,交延长线于.
求证:
17(全等)如图,等腰直角与等腰直角,为中点,连接、.
探究、的关系.
19(全等)如图,两个正方形和,点为的中点,连接交于点.
探究与的关系.
21.已知:如图,正方形和正方形,点是线段的中点.
⑴试说明线段与的关系.
⑵如图,若将上题中正方形绕点顺时针旋转度数(),其他条件不变,上述结论还正确吗?若正确,请你证明;若不正确,请说明理由.
22.如图1,正方形中,对角线、交于点.
⑴操作:将三角板中的角的顶点与点重合,使这个角落在的内部,两边分别与正方形的边、交于、.当、的位置发生变化时,请你通过测量并回答,每组、、三条线段中,哪一条线段是中始终最长.
⑵以、、这三条线段能否组成以为斜边的直角三角形?
若能,请你证明;若不能,请你说明理由.
⑶探究:如图2,,,点是斜线的中点,当角的顶点与点重合,使这个角在的内部绕点转动时,⑵中的结论是否仍然成立?请你证明.
23⑴如图1,操作:把正方形的对角线放在正方形的边的延长线上()
取线段的中点.
探究:线段、的关系,并加以证明.
⑵如图2,将正方形绕点旋转任意角度后,其他条件不变. 探究:线段、的关系,并加以证明.
一.割补法:
1.(全等)如图,点是中点,,求证:
2. (全等)如图,在中,,,,点是上一点,连结,过点做交于.
探究与的数量关系.
3. (全等)如图,在中,,点在上,点在的延长线上,且,交于点.
探究与的数量关系.
4. (全等)如图,在中,,、交于点.
探究与的数量关系.
5.(全等)如图,在中,平分,延长至点,使得,且.
探究与的数量关系.
6.(全等)如图,在中,,,为的中点,分别交、于、.
探究、的数量关系.
7. (全等)如图,,,.
探究:与之间的数量关系
10如图,直线、相交于点,点、点分别在直线、上,,连结,点是线段上任意一点(不与、重合),作,与的一边交于点,且.
⑴如图1,若,且时,猜想线段与的数量关系,并加以证明;
⑵如图2,若,时,猜想线段与的数量关系,并加以证明.
二.倍长中线法:
11. (全等)如图,点是中点,,求证:
13 (全等)如图,在中,,,是边的中线.求证:
15. (全等)如图,在中,平分,为的中点,交延长线于.
求证:
17(全等)如图,等腰直角与等腰直角,为中点,连接、.
探究、的关系.
19(全等)如图,两个正方形和,点为的中点,连接交于点.
探究与的关系.
21.已知:如图,正方形和正方形,点是线段的中点.
⑴试说明线段与的关系.
⑵如图,若将上题中正方形绕点顺时针旋转度数(),其他条件不变,上述结论还正确吗?若正确,请你证明;若不正确,请说明理由.
22.如图1,正方形中,对角线、交于点.
⑴操作:将三角板中的角的顶点与点重合,使这个角落在的内部,两边分别与正方形的边、交于、.当、的位置发生变化时,请你通过测量并回答,每组、、三条线段中,哪一条线段是中始终最长.
⑵以、、这三条线段能否组成以为斜边的直角三角形?
若能,请你证明;若不能,请你说明理由.
⑶探究:如图2,,,点是斜线的中点,当角的顶点与点重合,使这个角在的内部绕点转动时,⑵中的结论是否仍然成立?请你证明.
23⑴如图1,操作:把正方形的对角线放在正方形的边的延长线上()
取线段的中点.
探究:线段、的关系,并加以证明.
⑵如图2,将正方形绕点旋转任意角度后,其他条件不变. 探究:线段、的关系,并加以证明.
