11.3.1 多边形及其相关概念同步练习题(含解析)
文档属性
| 名称 | 11.3.1 多边形及其相关概念同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览



文档简介
11.3 多边形及其内角和
11.3.1 多边形及其相关概念
【知识重点】
1.多边形的定义:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形. 如果一个多边形由n 条线段组成,那么这个多边形就叫做n 边形.
2.相关概念
(1)内角:多边形相邻两边组成的角叫做它的内角.
(2)外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
(3)对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3.凸多边形:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,否则就是凹多边形. 本节只讨论凸多边形.
4.正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
特别解读
正多边形必备的两个条件:
(1) 各个角都相等;(2) 各条边都相等.
说明: 若一个多边形的各个角都相等或各条边都相等,则它不一定是正多边形.
特别解读
多边形的三个必要条件:
1. 线段在“同一平面内”;
2. 线段“不在同一直线上”且条数不少于3;
3. 首尾顺次相接.
【经典例题】
【例1】下列说法中,正确的有( )
①三角形是边数最少的多边形;
②等边三角形和长方形都是正多边形;
③ n边形有n条边、n个顶点、n个内角和n个外角;
④六边形从一个顶点出发可以画3 条对角线,所有的对角线共有9 条.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
【同步练习】
一、选择题
1.下列多边形中,不是凸多边形的是( )
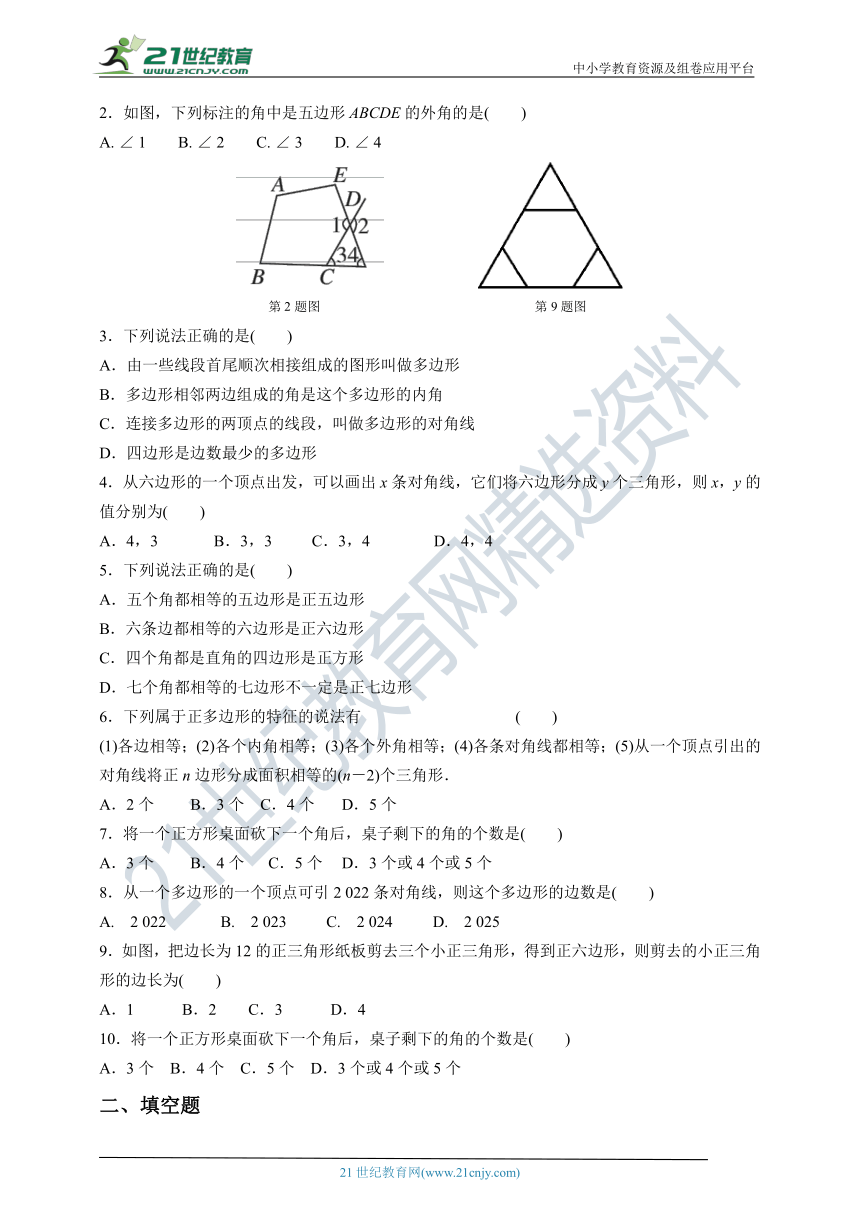
2.如图,下列标注的角中是五边形ABCDE的外角的是( )
A. ∠ 1 B. ∠ 2 C. ∠ 3 D. ∠ 4
第2题图 第9题图
3.下列说法正确的是( )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
5.下列说法正确的是( )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正方形
D.七个角都相等的七边形不一定是正七边形
6.下列属于正多边形的特征的说法有 ( )
(1)各边相等;(2)各个内角相等;(3)各个外角相等;(4)各条对角线都相等;(5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个 C.4个 D.5个
7.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( )
A.3个 B.4个 C.5个 D.3个或4个或5个
8.从一个多边形的一个顶点可引2 022条对角线,则这个多边形的边数是( )
A. 2 022 B. 2 023 C. 2 024 D. 2 025
9.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为( )
A.1 B.2 C.3 D.4
10.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( )
A.3个 B.4个 C.5个 D.3个或4个或5个
二、填空题
11.各个角________,各条边________的多边形叫做正多边形.
12.下列图形中:①等腰三角形;②等边三角形;③矩形;④线段;⑤角;⑥圆;⑦正方形;⑧六边形.其中是正多边形的有: (填序号).
13.从五边形的一个顶点出发有 条对角线.
14.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
15.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,则此多边形为 .
三、解答题
16.“菱形是正多边形”这句话是否正确?为什么?
17.已知,从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边之长.
18.如图,在边长为1的小正方形组成的方格纸中,将各顶点都在格点上的多边形称为格点多边形.奥地利数学家皮克证明了格点多边形的面积公式为S=a+b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.求图中格点多边形的面积.
19.观察下面图形,解答下列问题:
(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整.
边 数 3 4 5 6 7 … n
对角线条数 0 2 5 …
20.试比较图中两个几何图形的异同,请分别写出两个相同点和两个不同点,例如,相同点:正方形的对角线相等,正五边形的对角线也相等;不同点:正方形有两条对角线、正五边形有五条对角线.
相同点:
(1)__________;(2)__________.
不同点:
(1)___________;(2)_____________.
21.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,OD,可以得到几个三角形?它与边数有何关系?
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】下列说法中,正确的有( )
①三角形是边数最少的多边形;
②等边三角形和长方形都是正多边形;
③ n边形有n条边、n个顶点、n个内角和n个外角;
④六边形从一个顶点出发可以画3 条对角线,所有的对角线共有9 条.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
解题秘方:利用多边形的有关概念进行辨析.
解:①三角形是边数最少的多边形,正确;②等边三角形是正多边形,但长方形不是正多边形,不正确;③ n边形有n条边、n个顶点、n个内角和2n个外角,不正确;④根据对角线的定义画出六边形的对角线可知,从一个顶点出发可以画3 条对角线,所有的对角线共有9 条,正确.
答案:B
知识归纳:从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,n 边形一共有条对角线.
【同步练习】
一、选择题
1.下列多边形中,不是凸多边形的是( B )
2.如图,下列标注的角中是五边形ABCDE的外角的是( C )
A. ∠ 1 B. ∠ 2 C. ∠ 3 D. ∠ 4
第2题图 第9题图
3.下列说法正确的是( B )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为( C )
A.4,3 B.3,3 C.3,4 D.4,4
5.下列说法正确的是( D )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正方形
D.七个角都相等的七边形不一定是正七边形
6.下列属于正多边形的特征的说法有 ( B )
(1)各边相等;(2)各个内角相等;(3)各个外角相等;(4)各条对角线都相等;(5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个 C.4个 D.5个
7.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( D )
A.3个 B.4个 C.5个 D.3个或4个或5个
8.从一个多边形的一个顶点可引2 022条对角线,则这个多边形的边数是( D )
A. 2 022 B. 2 023 C. 2 024 D. 2 025
9.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为( D )
A.1 B.2 C.3 D.4
【解析】由题可知剪去的小正三角形的边长与正六边形的边长相等,∴剪去的小正三角形的边长为=4.
10.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( D )
A.3个 B.4个 C.5个 D.3个或4个或5个
【解析】如图所示.
由图可知,桌子剩下的角的个数是3个或4个或5个.
二、填空题
11.各个角________,各条边________的多边形叫做正多边形.
【答案】都相等 都相等
12.下列图形中:①等腰三角形;②等边三角形;③矩形;④线段;⑤角;⑥圆;⑦正方形;⑧六边形.其中是正多边形的有: (填序号).
【答案】②⑦
13.从五边形的一个顶点出发有 条对角线.
【答案】2
14.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
【答案】6
15.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,则此多边形为 .
【答案】六边形
三、解答题
16.“菱形是正多边形”这句话是否正确?为什么?
解:不正确.因为菱形不一定是正多边形,菱形的四条边相等,但四个角不一定相等.
17.已知,从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边之长.
解:设这个多边形的边数为n,则n-3=4,∴n=7.设这个多边形较小的边长为x,则
x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)=56,7x=35,∴x=5.
∴这个多边形的各边之长分别为5,6,7,8,9,10,11.
18.如图,在边长为1的小正方形组成的方格纸中,将各顶点都在格点上的多边形称为格点多边形.奥地利数学家皮克证明了格点多边形的面积公式为S=a+b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.求图中格点多边形的面积.
解:由题意,得a=5,b=5,
∴S=a+b-1=5+-1=.
19.观察下面图形,解答下列问题:
(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整.
边 数 3 4 5 6 7 … n
对角线条数 0 2 5 …
解 (1)
(2)
边数 3 4 5 6 7 … n
对角线条数 0 2 5 9 14 … n(n-3)
20.试比较图中两个几何图形的异同,请分别写出两个相同点和两个不同点,例如,相同点:正方形的对角线相等,正五边形的对角线也相等;不同点:正方形有两条对角线、正五边形有五条对角线.
相同点:
(1)__________;(2)__________.
不同点:
(1)___________;(2)_____________.
答案不唯一,如:
相同点:(1)正方形的各边都相等,正五边形的各边也都相等 (2)正方形的各角都相等,正五边形的各角也都相等
不同点:(1)正方形每个内角的度数与正五边形每个内角的度数不相等 (2)边数不相等
21.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,OD,可以得到几个三角形?它与边数有何关系?
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
解:(1)4个,与边数相等.
(2)4个,为边数减1.
(3)4个,为边数减2.
11.3.1 多边形及其相关概念
【知识重点】
1.多边形的定义:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形. 如果一个多边形由n 条线段组成,那么这个多边形就叫做n 边形.
2.相关概念
(1)内角:多边形相邻两边组成的角叫做它的内角.
(2)外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
(3)对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3.凸多边形:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,否则就是凹多边形. 本节只讨论凸多边形.
4.正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
特别解读
正多边形必备的两个条件:
(1) 各个角都相等;(2) 各条边都相等.
说明: 若一个多边形的各个角都相等或各条边都相等,则它不一定是正多边形.
特别解读
多边形的三个必要条件:
1. 线段在“同一平面内”;
2. 线段“不在同一直线上”且条数不少于3;
3. 首尾顺次相接.
【经典例题】
【例1】下列说法中,正确的有( )
①三角形是边数最少的多边形;
②等边三角形和长方形都是正多边形;
③ n边形有n条边、n个顶点、n个内角和n个外角;
④六边形从一个顶点出发可以画3 条对角线,所有的对角线共有9 条.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
【同步练习】
一、选择题
1.下列多边形中,不是凸多边形的是( )
2.如图,下列标注的角中是五边形ABCDE的外角的是( )
A. ∠ 1 B. ∠ 2 C. ∠ 3 D. ∠ 4
第2题图 第9题图
3.下列说法正确的是( )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
5.下列说法正确的是( )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正方形
D.七个角都相等的七边形不一定是正七边形
6.下列属于正多边形的特征的说法有 ( )
(1)各边相等;(2)各个内角相等;(3)各个外角相等;(4)各条对角线都相等;(5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个 C.4个 D.5个
7.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( )
A.3个 B.4个 C.5个 D.3个或4个或5个
8.从一个多边形的一个顶点可引2 022条对角线,则这个多边形的边数是( )
A. 2 022 B. 2 023 C. 2 024 D. 2 025
9.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为( )
A.1 B.2 C.3 D.4
10.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( )
A.3个 B.4个 C.5个 D.3个或4个或5个
二、填空题
11.各个角________,各条边________的多边形叫做正多边形.
12.下列图形中:①等腰三角形;②等边三角形;③矩形;④线段;⑤角;⑥圆;⑦正方形;⑧六边形.其中是正多边形的有: (填序号).
13.从五边形的一个顶点出发有 条对角线.
14.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
15.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,则此多边形为 .
三、解答题
16.“菱形是正多边形”这句话是否正确?为什么?
17.已知,从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边之长.
18.如图,在边长为1的小正方形组成的方格纸中,将各顶点都在格点上的多边形称为格点多边形.奥地利数学家皮克证明了格点多边形的面积公式为S=a+b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.求图中格点多边形的面积.
19.观察下面图形,解答下列问题:
(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整.
边 数 3 4 5 6 7 … n
对角线条数 0 2 5 …
20.试比较图中两个几何图形的异同,请分别写出两个相同点和两个不同点,例如,相同点:正方形的对角线相等,正五边形的对角线也相等;不同点:正方形有两条对角线、正五边形有五条对角线.
相同点:
(1)__________;(2)__________.
不同点:
(1)___________;(2)_____________.
21.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,OD,可以得到几个三角形?它与边数有何关系?
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】下列说法中,正确的有( )
①三角形是边数最少的多边形;
②等边三角形和长方形都是正多边形;
③ n边形有n条边、n个顶点、n个内角和n个外角;
④六边形从一个顶点出发可以画3 条对角线,所有的对角线共有9 条.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
解题秘方:利用多边形的有关概念进行辨析.
解:①三角形是边数最少的多边形,正确;②等边三角形是正多边形,但长方形不是正多边形,不正确;③ n边形有n条边、n个顶点、n个内角和2n个外角,不正确;④根据对角线的定义画出六边形的对角线可知,从一个顶点出发可以画3 条对角线,所有的对角线共有9 条,正确.
答案:B
知识归纳:从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n 边形分为(n-2)个三角形,n 边形一共有条对角线.
【同步练习】
一、选择题
1.下列多边形中,不是凸多边形的是( B )
2.如图,下列标注的角中是五边形ABCDE的外角的是( C )
A. ∠ 1 B. ∠ 2 C. ∠ 3 D. ∠ 4
第2题图 第9题图
3.下列说法正确的是( B )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形相邻两边组成的角是这个多边形的内角
C.连接多边形的两顶点的线段,叫做多边形的对角线
D.四边形是边数最少的多边形
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为( C )
A.4,3 B.3,3 C.3,4 D.4,4
5.下列说法正确的是( D )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正方形
D.七个角都相等的七边形不一定是正七边形
6.下列属于正多边形的特征的说法有 ( B )
(1)各边相等;(2)各个内角相等;(3)各个外角相等;(4)各条对角线都相等;(5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个 C.4个 D.5个
7.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( D )
A.3个 B.4个 C.5个 D.3个或4个或5个
8.从一个多边形的一个顶点可引2 022条对角线,则这个多边形的边数是( D )
A. 2 022 B. 2 023 C. 2 024 D. 2 025
9.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为( D )
A.1 B.2 C.3 D.4
【解析】由题可知剪去的小正三角形的边长与正六边形的边长相等,∴剪去的小正三角形的边长为=4.
10.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( D )
A.3个 B.4个 C.5个 D.3个或4个或5个
【解析】如图所示.
由图可知,桌子剩下的角的个数是3个或4个或5个.
二、填空题
11.各个角________,各条边________的多边形叫做正多边形.
【答案】都相等 都相等
12.下列图形中:①等腰三角形;②等边三角形;③矩形;④线段;⑤角;⑥圆;⑦正方形;⑧六边形.其中是正多边形的有: (填序号).
【答案】②⑦
13.从五边形的一个顶点出发有 条对角线.
【答案】2
14.过八边形的一个顶点画对角线,把这个八边形分割成 个三角形.
【答案】6
15.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,则此多边形为 .
【答案】六边形
三、解答题
16.“菱形是正多边形”这句话是否正确?为什么?
解:不正确.因为菱形不一定是正多边形,菱形的四条边相等,但四个角不一定相等.
17.已知,从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边之长.
解:设这个多边形的边数为n,则n-3=4,∴n=7.设这个多边形较小的边长为x,则
x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)=56,7x=35,∴x=5.
∴这个多边形的各边之长分别为5,6,7,8,9,10,11.
18.如图,在边长为1的小正方形组成的方格纸中,将各顶点都在格点上的多边形称为格点多边形.奥地利数学家皮克证明了格点多边形的面积公式为S=a+b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.求图中格点多边形的面积.
解:由题意,得a=5,b=5,
∴S=a+b-1=5+-1=.
19.观察下面图形,解答下列问题:
(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整.
边 数 3 4 5 6 7 … n
对角线条数 0 2 5 …
解 (1)
(2)
边数 3 4 5 6 7 … n
对角线条数 0 2 5 9 14 … n(n-3)
20.试比较图中两个几何图形的异同,请分别写出两个相同点和两个不同点,例如,相同点:正方形的对角线相等,正五边形的对角线也相等;不同点:正方形有两条对角线、正五边形有五条对角线.
相同点:
(1)__________;(2)__________.
不同点:
(1)___________;(2)_____________.
答案不唯一,如:
相同点:(1)正方形的各边都相等,正五边形的各边也都相等 (2)正方形的各角都相等,正五边形的各角也都相等
不同点:(1)正方形每个内角的度数与正五边形每个内角的度数不相等 (2)边数不相等
21.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,OD,可以得到几个三角形?它与边数有何关系?
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
解:(1)4个,与边数相等.
(2)4个,为边数减1.
(3)4个,为边数减2.
