第11章 三角形习题课 角度计算的几种常见应用类型(含答案)
文档属性
| 名称 | 第11章 三角形习题课 角度计算的几种常见应用类型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 19:51:03 | ||
图片预览


文档简介
第11章 三角形 习题课 角度计算的几种常见应用类型
三角形内角和与外角和有着广泛的应用,利用它们可以解决有关角的很多问题,一般可用于直接计算角度、三角尺中求角度、与平行线的性质综合求角度、折叠问题中求角度等.
【同步练习】
类型1 直接计算角度
1.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
2.如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于 ( )
A.120° B.115° C.110° D.105°
3.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B=_________.
类型2 三角尺中求角度
4.如图,将一副三角板叠放在一块,AC与EF所夹的钝角的度数为 .
5.一副三角尺如图所示摆放,则∠α与∠β的数量关系为( )
A.∠α+∠β=180° B.∠α+∠β=225°
C.∠α+∠β=270° D.∠α=∠β
6.一副三角尺如图放置,则∠1+∠2的度数和为( )
A.30° B.45° C.60° D.75°
类型3 与平行线的性质综合求角度
7.如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为_________.
8.如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45° B.50° C.55° D.80°
9.如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,则∠B的度数为 .
类型4 折叠中求角度
10.如图,在△ABC中,∠C=90°,∠B=68°,点D,E分别在AB,AC上,将△ADE沿DE折叠,使点A落在点F处,则∠BDF-∠CEF=_________.
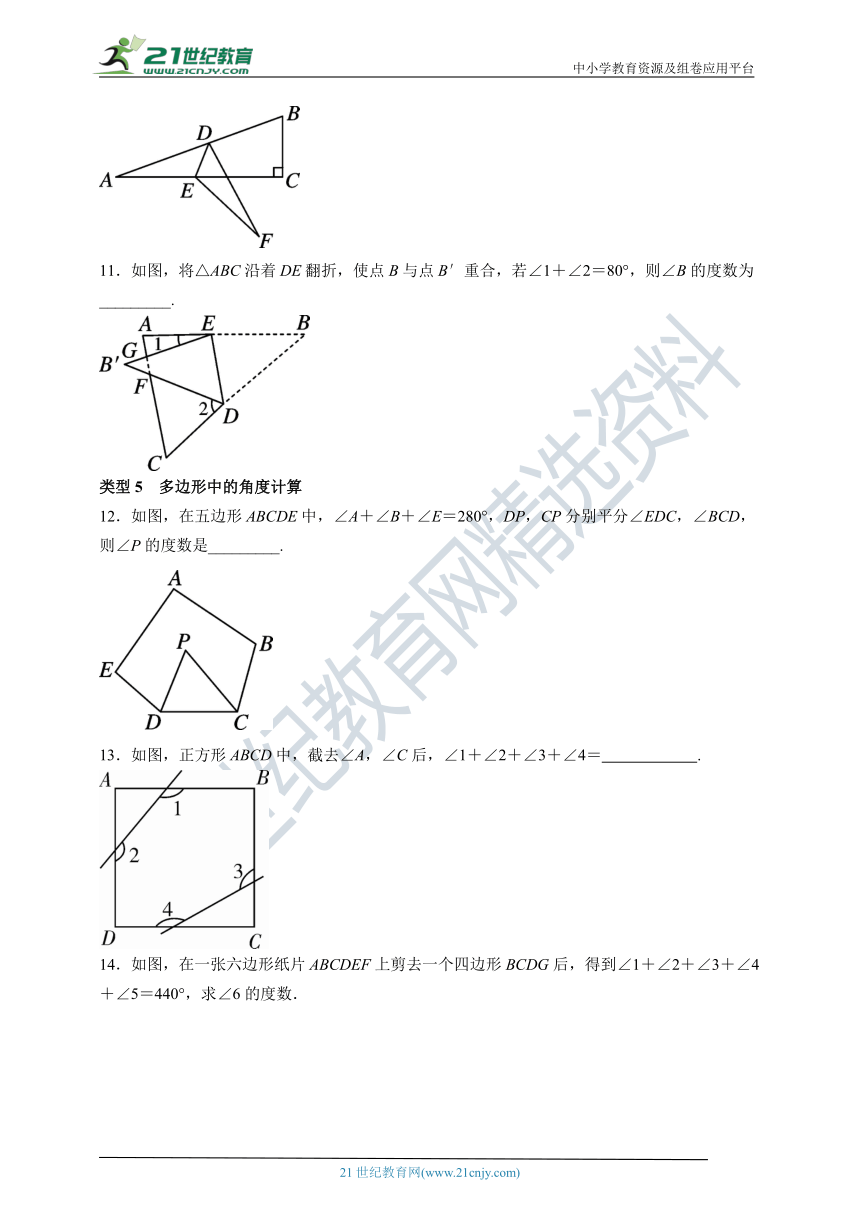
11.如图,将△ABC沿着DE翻折,使点B与点B′重合,若∠1+∠2=80°,则∠B的度数为_________.
类型5 多边形中的角度计算
12.如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是_________.
13.如图,正方形ABCD中,截去∠A,∠C后,∠1+∠2+∠3+∠4= .
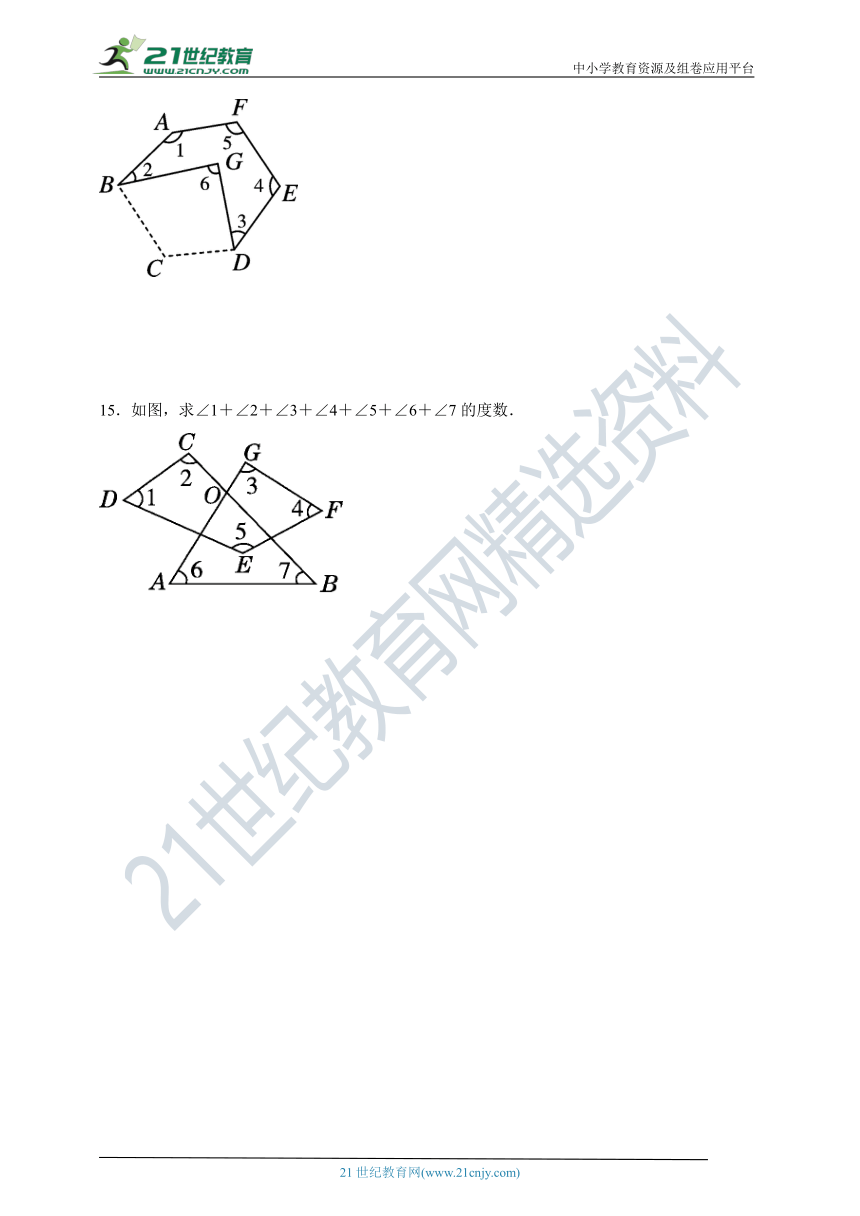
14.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,求∠6的度数.
15.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【同步练习】
类型1 直接计算角度
1.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( C )
A.40° B.45° C.50° D.55°
2.如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于 ( C )
A.120° B.115° C.110° D.105°
3.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B=_________.
【答案】60°
类型2 三角尺中求角度
4.如图,将一副三角板叠放在一块,AC与EF所夹的钝角的度数为 .
【答案】165°
5.一副三角尺如图所示摆放,则∠α与∠β的数量关系为( B )
A.∠α+∠β=180° B.∠α+∠β=225°
C.∠α+∠β=270° D.∠α=∠β
6.一副三角尺如图放置,则∠1+∠2的度数和为( B )
A.30° B.45° C.60° D.75°
类型3 与平行线的性质综合求角度
7.如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为_________.
【答案】10°
8.如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( A )
A.45° B.50° C.55° D.80°
9.如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,则∠B的度数为 .
【答案】30°
类型4 折叠中求角度
10.如图,在△ABC中,∠C=90°,∠B=68°,点D,E分别在AB,AC上,将△ADE沿DE折叠,使点A落在点F处,则∠BDF-∠CEF=_________.
【答案】44°
11.如图,将△ABC沿着DE翻折,使点B与点B′重合,若∠1+∠2=80°,则∠B的度数为_________.
【答案】40°
类型5 多边形中的角度计算
12.如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是_________.
【答案】50°
13.如图,正方形ABCD中,截去∠A,∠C后,∠1+∠2+∠3+∠4= .
【答案】540°
14.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,求∠6的度数.
解:∵六边形ABCDEF的内角和为180°×(6-2)=720°,且∠1+∠2+∠3+∠4+∠5=440°,∴∠GBC+∠C+∠CDG=720°-440°=280°,
∴∠6=360°-(∠GBC+∠C+∠CDG)=360°-280°=80°.
15.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
【解析】连接CG,利用转化思想,将求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数转化为求多边形CDEFG的内角和.
解:连接CG.
在△COG和△AOB中,∠COG=∠AOB,
∴∠6+∠7=∠OCG+∠OGC.
在五边形CDEFG中,∠1+∠2+∠3+∠4+∠5+∠OCG+∠OGC=540°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
三角形内角和与外角和有着广泛的应用,利用它们可以解决有关角的很多问题,一般可用于直接计算角度、三角尺中求角度、与平行线的性质综合求角度、折叠问题中求角度等.
【同步练习】
类型1 直接计算角度
1.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
2.如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于 ( )
A.120° B.115° C.110° D.105°
3.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B=_________.
类型2 三角尺中求角度
4.如图,将一副三角板叠放在一块,AC与EF所夹的钝角的度数为 .
5.一副三角尺如图所示摆放,则∠α与∠β的数量关系为( )
A.∠α+∠β=180° B.∠α+∠β=225°
C.∠α+∠β=270° D.∠α=∠β
6.一副三角尺如图放置,则∠1+∠2的度数和为( )
A.30° B.45° C.60° D.75°
类型3 与平行线的性质综合求角度
7.如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为_________.
8.如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45° B.50° C.55° D.80°
9.如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,则∠B的度数为 .
类型4 折叠中求角度
10.如图,在△ABC中,∠C=90°,∠B=68°,点D,E分别在AB,AC上,将△ADE沿DE折叠,使点A落在点F处,则∠BDF-∠CEF=_________.
11.如图,将△ABC沿着DE翻折,使点B与点B′重合,若∠1+∠2=80°,则∠B的度数为_________.
类型5 多边形中的角度计算
12.如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是_________.
13.如图,正方形ABCD中,截去∠A,∠C后,∠1+∠2+∠3+∠4= .
14.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,求∠6的度数.
15.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【同步练习】
类型1 直接计算角度
1.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( C )
A.40° B.45° C.50° D.55°
2.如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于 ( C )
A.120° B.115° C.110° D.105°
3.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B=_________.
【答案】60°
类型2 三角尺中求角度
4.如图,将一副三角板叠放在一块,AC与EF所夹的钝角的度数为 .
【答案】165°
5.一副三角尺如图所示摆放,则∠α与∠β的数量关系为( B )
A.∠α+∠β=180° B.∠α+∠β=225°
C.∠α+∠β=270° D.∠α=∠β
6.一副三角尺如图放置,则∠1+∠2的度数和为( B )
A.30° B.45° C.60° D.75°
类型3 与平行线的性质综合求角度
7.如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为_________.
【答案】10°
8.如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( A )
A.45° B.50° C.55° D.80°
9.如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,则∠B的度数为 .
【答案】30°
类型4 折叠中求角度
10.如图,在△ABC中,∠C=90°,∠B=68°,点D,E分别在AB,AC上,将△ADE沿DE折叠,使点A落在点F处,则∠BDF-∠CEF=_________.
【答案】44°
11.如图,将△ABC沿着DE翻折,使点B与点B′重合,若∠1+∠2=80°,则∠B的度数为_________.
【答案】40°
类型5 多边形中的角度计算
12.如图,在五边形ABCDE中,∠A+∠B+∠E=280°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是_________.
【答案】50°
13.如图,正方形ABCD中,截去∠A,∠C后,∠1+∠2+∠3+∠4= .
【答案】540°
14.如图,在一张六边形纸片ABCDEF上剪去一个四边形BCDG后,得到∠1+∠2+∠3+∠4+∠5=440°,求∠6的度数.
解:∵六边形ABCDEF的内角和为180°×(6-2)=720°,且∠1+∠2+∠3+∠4+∠5=440°,∴∠GBC+∠C+∠CDG=720°-440°=280°,
∴∠6=360°-(∠GBC+∠C+∠CDG)=360°-280°=80°.
15.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
【解析】连接CG,利用转化思想,将求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数转化为求多边形CDEFG的内角和.
解:连接CG.
在△COG和△AOB中,∠COG=∠AOB,
∴∠6+∠7=∠OCG+∠OGC.
在五边形CDEFG中,∠1+∠2+∠3+∠4+∠5+∠OCG+∠OGC=540°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
