第11章 三角形习题课 三角形中线段的相关应用(含答案)
文档属性
| 名称 | 第11章 三角形习题课 三角形中线段的相关应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 19:49:07 | ||
图片预览


文档简介
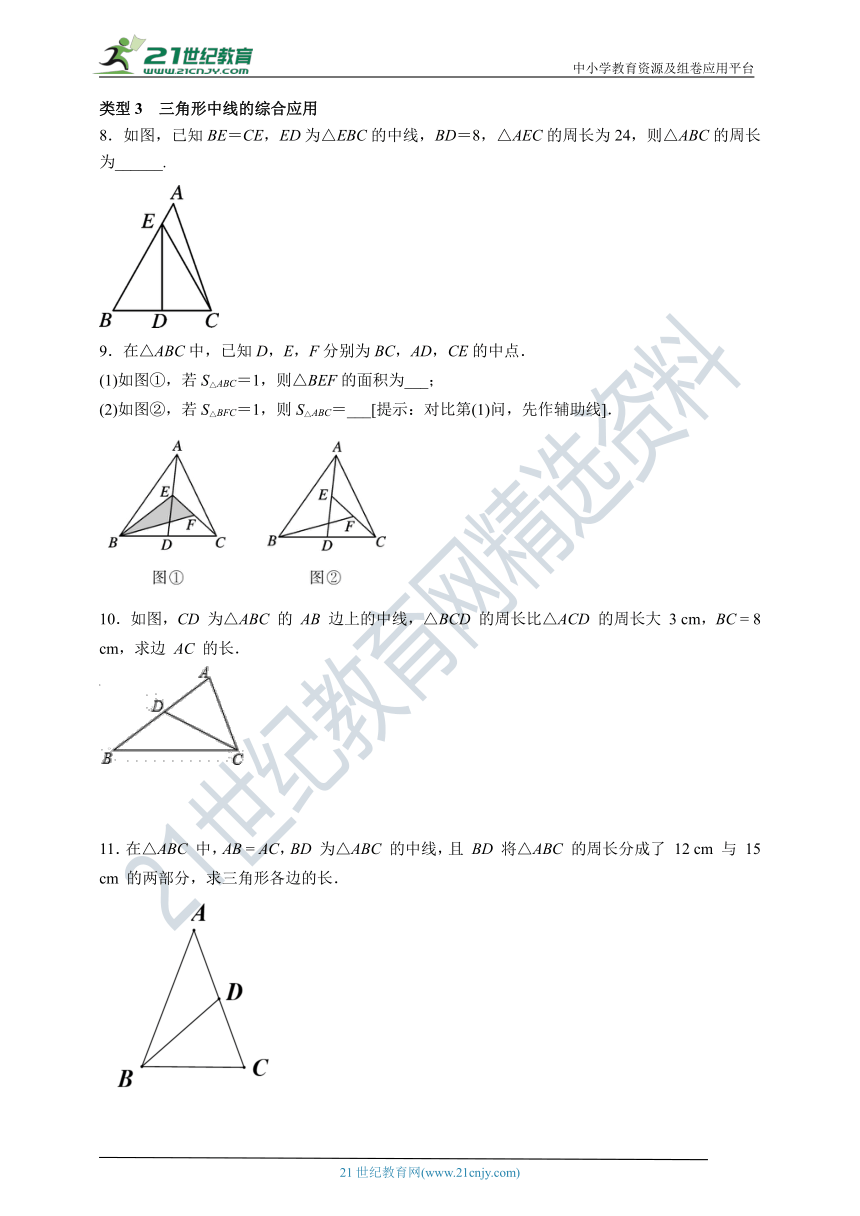
第11章 三角形 习题课 三角形中线段的相关应用
【同步练习】
类型1 三角形的三边关系
1.已知不等边三角形的一边等于5,另一边等于3,若第三边长为奇数,则周长等于( )
A.13 B.11 C.11,13或15 D.15
2.【2020·徐州】若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( )
A.2 cm B.3 cm C.6 cm D.9 cm
3.以长度分别为3、4、x -5的线段为边可以组成一个三角形,那么 x 的取值范围是 .
4.等腰三角形的周长为16,其一边长为6,求另两边长.
类型2 三角形高的综合应用
5.下列四个图形中,线段BE是△ABC的高的是( )
6.如图,在△ABC中,BC=4,AC=5,若BC边上的高AD=4.
(1)求△ABC的面积及AC边上的高BE的长;
(2)求AD∶BE的值.
7.如图,在△ABC 中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为E,F,G.
求证:DE+DF=BG.
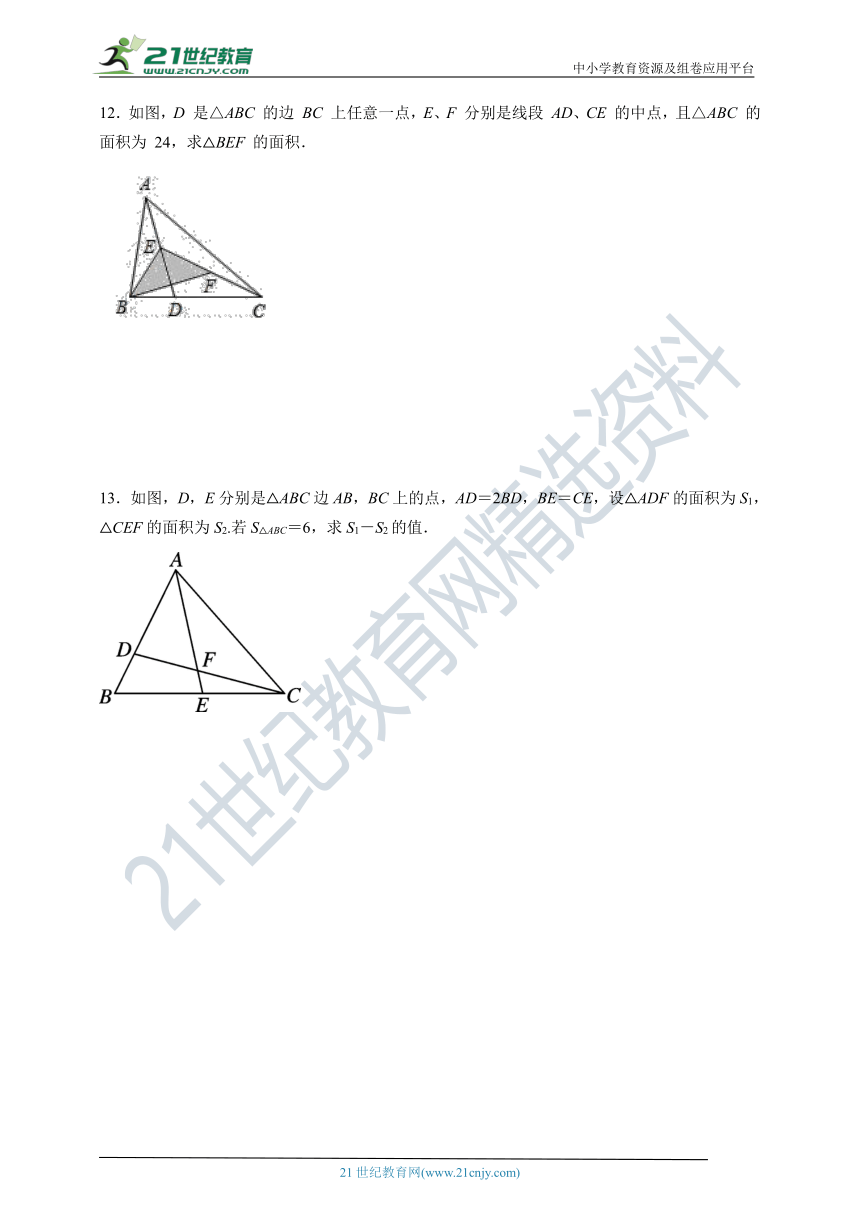
类型3 三角形中线的综合应用
8.如图,已知BE=CE,ED为△EBC的中线,BD=8,△AEC的周长为24,则△ABC的周长为______.
9.在△ABC中,已知D,E,F分别为BC,AD,CE的中点.
(1)如图①,若S△ABC=1,则△BEF的面积为___;
(2)如图②,若S△BFC=1,则S△ABC=___[提示:对比第(1)问,先作辅助线].
10.如图,CD 为△ABC 的 AB 边上的中线,△BCD 的周长比△ACD 的周长大 3 cm,BC = 8 cm,求边 AC 的长.
11.在△ABC 中,AB = AC,BD 为△ABC 的中线,且 BD 将△ABC 的周长分成了 12 cm 与 15 cm 的两部分,求三角形各边的长.
12.如图,D 是△ABC 的边 BC 上任意一点,E、F 分别是线段 AD、CE 的中点,且△ABC 的面积为 24,求△BEF 的面积.
13.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2.若S△ABC=6,求S1-S2的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【同步练习】
类型1 三角形的三边关系
1.已知不等边三角形的一边等于5,另一边等于3,若第三边长为奇数,则周长等于( D )
A.13 B.11 C.11,13或15 D.15
2.【2020·徐州】若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( C )
A.2 cm B.3 cm C.6 cm D.9 cm
3.以长度分别为3、4、x -5的线段为边可以组成一个三角形,那么 x 的取值范围是 .
【答案】6 < x < 12
4.等腰三角形的周长为16,其一边长为6,求另两边长.
解:由于题中没有指明边长为 6 的边是底还是腰,
故应分两种情况讨论:
①当 6 为底边长时,腰长为 (16 - 6)÷2 = 5,这时另两边长分别为 5,5,符合三边关系;
当 6 为腰长时,底边长为 16 - 6 - 6 = 4,这时另两边长分别为 6,4,符合三边关系.
综上所述,另两边长为 5,5 或 6,4.
类型2 三角形高的综合应用
5.下列四个图形中,线段BE是△ABC的高的是( C )
6.如图,在△ABC中,BC=4,AC=5,若BC边上的高AD=4.
(1)求△ABC的面积及AC边上的高BE的长;
(2)求AD∶BE的值.
解:(1)S△ABC=BC·AD=×4×4=8.
∵S△ABC=AC·BE=×5×BE=8,∴BE=.
(2)AD∶BE=4∶=.
7.如图,在△ABC 中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为E,F,G.
求证:DE+DF=BG.
证明:
连接AD.∵S△ABC=S△ABD+S△ADC,
∴AC·BG=AB·DE+AC·DF.
又∵AB=AC,∴DE+DF=BG.
类型3 三角形中线的综合应用
8.如图,已知BE=CE,ED为△EBC的中线,BD=8,△AEC的周长为24,则△ABC的周长为______.
【答案】40
9.在△ABC中,已知D,E,F分别为BC,AD,CE的中点.
(1)如图①,若S△ABC=1,则△BEF的面积为___;
(2)如图②,若S△BFC=1,则S△ABC=___[提示:对比第(1)问,先作辅助线].
【答案】 4
10.如图,CD 为△ABC 的 AB 边上的中线,△BCD 的周长比△ACD 的周长大 3 cm,BC = 8 cm,求边 AC 的长.
解:∵ CD 为△ABC 的 AB 边上的中线,
∴ AD = BD.
∵△BCD 的周长比△ACD 的周长大 3 cm,
∴ (BC + BD + CD)-(AC + AD + CD) = 3.
∴ BC-AC = 3.
∵ BC = 8 cm,
∴ AC = 5 cm.
11.在△ABC 中,AB = AC,BD 为△ABC 的中线,且 BD 将△ABC 的周长分成了 12 cm 与 15 cm 的两部分,求三角形各边的长.
解:如图,依题意设 AD = CD = x cm,
则 AB = AC = 2x cm.
当 x + 2x = 12,BC + x = 15 时,解得 x = 4,BC = 11 cm,
此时 AB = AC = 8 cm,BC = 11 cm,符合题意;
当 x + 2x = 15,BC + x = 12 时,解得 x = 5,BC = 7 cm,
此时 AB = AC = 10 cm,BC = 7 cm,符合题意.
12.如图,D 是△ABC 的边 BC 上任意一点,E、F 分别是线段 AD、CE 的中点,且△ABC 的面积为 24,求△BEF 的面积.
解:∵ 点 E 是 AD 的中点,
∴ S△DBE =S△ABD,S△DCE =S△ADC.
∴ S△DBE + S△DCE =S△ABC =×24 = 12,即 S△BCE = 12.
∵ 点 F 是 CE 的中点,∴ S△BEF =S△BCE =×12 = 6.
13.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2.若S△ABC=6,求S1-S2的值.
解:∵BE=CE,
∴CE=BC.
∵S△ABC=6,
∴S△AEC=S△ABC=×6=3.
∵AD=2BD,S△ABC=6,
∴S△ACD=S△ABC=4.
∴S1-S2=(S△ACD-S△AFC)-(S△AEC-S△AFC)=S△ACD-S△AEC=4-3=1.
即S1-S2的值为1.
【同步练习】
类型1 三角形的三边关系
1.已知不等边三角形的一边等于5,另一边等于3,若第三边长为奇数,则周长等于( )
A.13 B.11 C.11,13或15 D.15
2.【2020·徐州】若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( )
A.2 cm B.3 cm C.6 cm D.9 cm
3.以长度分别为3、4、x -5的线段为边可以组成一个三角形,那么 x 的取值范围是 .
4.等腰三角形的周长为16,其一边长为6,求另两边长.
类型2 三角形高的综合应用
5.下列四个图形中,线段BE是△ABC的高的是( )
6.如图,在△ABC中,BC=4,AC=5,若BC边上的高AD=4.
(1)求△ABC的面积及AC边上的高BE的长;
(2)求AD∶BE的值.
7.如图,在△ABC 中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为E,F,G.
求证:DE+DF=BG.
类型3 三角形中线的综合应用
8.如图,已知BE=CE,ED为△EBC的中线,BD=8,△AEC的周长为24,则△ABC的周长为______.
9.在△ABC中,已知D,E,F分别为BC,AD,CE的中点.
(1)如图①,若S△ABC=1,则△BEF的面积为___;
(2)如图②,若S△BFC=1,则S△ABC=___[提示:对比第(1)问,先作辅助线].
10.如图,CD 为△ABC 的 AB 边上的中线,△BCD 的周长比△ACD 的周长大 3 cm,BC = 8 cm,求边 AC 的长.
11.在△ABC 中,AB = AC,BD 为△ABC 的中线,且 BD 将△ABC 的周长分成了 12 cm 与 15 cm 的两部分,求三角形各边的长.
12.如图,D 是△ABC 的边 BC 上任意一点,E、F 分别是线段 AD、CE 的中点,且△ABC 的面积为 24,求△BEF 的面积.
13.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2.若S△ABC=6,求S1-S2的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【同步练习】
类型1 三角形的三边关系
1.已知不等边三角形的一边等于5,另一边等于3,若第三边长为奇数,则周长等于( D )
A.13 B.11 C.11,13或15 D.15
2.【2020·徐州】若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( C )
A.2 cm B.3 cm C.6 cm D.9 cm
3.以长度分别为3、4、x -5的线段为边可以组成一个三角形,那么 x 的取值范围是 .
【答案】6 < x < 12
4.等腰三角形的周长为16,其一边长为6,求另两边长.
解:由于题中没有指明边长为 6 的边是底还是腰,
故应分两种情况讨论:
①当 6 为底边长时,腰长为 (16 - 6)÷2 = 5,这时另两边长分别为 5,5,符合三边关系;
当 6 为腰长时,底边长为 16 - 6 - 6 = 4,这时另两边长分别为 6,4,符合三边关系.
综上所述,另两边长为 5,5 或 6,4.
类型2 三角形高的综合应用
5.下列四个图形中,线段BE是△ABC的高的是( C )
6.如图,在△ABC中,BC=4,AC=5,若BC边上的高AD=4.
(1)求△ABC的面积及AC边上的高BE的长;
(2)求AD∶BE的值.
解:(1)S△ABC=BC·AD=×4×4=8.
∵S△ABC=AC·BE=×5×BE=8,∴BE=.
(2)AD∶BE=4∶=.
7.如图,在△ABC 中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为E,F,G.
求证:DE+DF=BG.
证明:
连接AD.∵S△ABC=S△ABD+S△ADC,
∴AC·BG=AB·DE+AC·DF.
又∵AB=AC,∴DE+DF=BG.
类型3 三角形中线的综合应用
8.如图,已知BE=CE,ED为△EBC的中线,BD=8,△AEC的周长为24,则△ABC的周长为______.
【答案】40
9.在△ABC中,已知D,E,F分别为BC,AD,CE的中点.
(1)如图①,若S△ABC=1,则△BEF的面积为___;
(2)如图②,若S△BFC=1,则S△ABC=___[提示:对比第(1)问,先作辅助线].
【答案】 4
10.如图,CD 为△ABC 的 AB 边上的中线,△BCD 的周长比△ACD 的周长大 3 cm,BC = 8 cm,求边 AC 的长.
解:∵ CD 为△ABC 的 AB 边上的中线,
∴ AD = BD.
∵△BCD 的周长比△ACD 的周长大 3 cm,
∴ (BC + BD + CD)-(AC + AD + CD) = 3.
∴ BC-AC = 3.
∵ BC = 8 cm,
∴ AC = 5 cm.
11.在△ABC 中,AB = AC,BD 为△ABC 的中线,且 BD 将△ABC 的周长分成了 12 cm 与 15 cm 的两部分,求三角形各边的长.
解:如图,依题意设 AD = CD = x cm,
则 AB = AC = 2x cm.
当 x + 2x = 12,BC + x = 15 时,解得 x = 4,BC = 11 cm,
此时 AB = AC = 8 cm,BC = 11 cm,符合题意;
当 x + 2x = 15,BC + x = 12 时,解得 x = 5,BC = 7 cm,
此时 AB = AC = 10 cm,BC = 7 cm,符合题意.
12.如图,D 是△ABC 的边 BC 上任意一点,E、F 分别是线段 AD、CE 的中点,且△ABC 的面积为 24,求△BEF 的面积.
解:∵ 点 E 是 AD 的中点,
∴ S△DBE =S△ABD,S△DCE =S△ADC.
∴ S△DBE + S△DCE =S△ABC =×24 = 12,即 S△BCE = 12.
∵ 点 F 是 CE 的中点,∴ S△BEF =S△BCE =×12 = 6.
13.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2.若S△ABC=6,求S1-S2的值.
解:∵BE=CE,
∴CE=BC.
∵S△ABC=6,
∴S△AEC=S△ABC=×6=3.
∵AD=2BD,S△ABC=6,
∴S△ACD=S△ABC=4.
∴S1-S2=(S△ACD-S△AFC)-(S△AEC-S△AFC)=S△ACD-S△AEC=4-3=1.
即S1-S2的值为1.
