第11章 三角形章末复习题(含答案)
图片预览


文档简介
第11章 三角形 章末复习
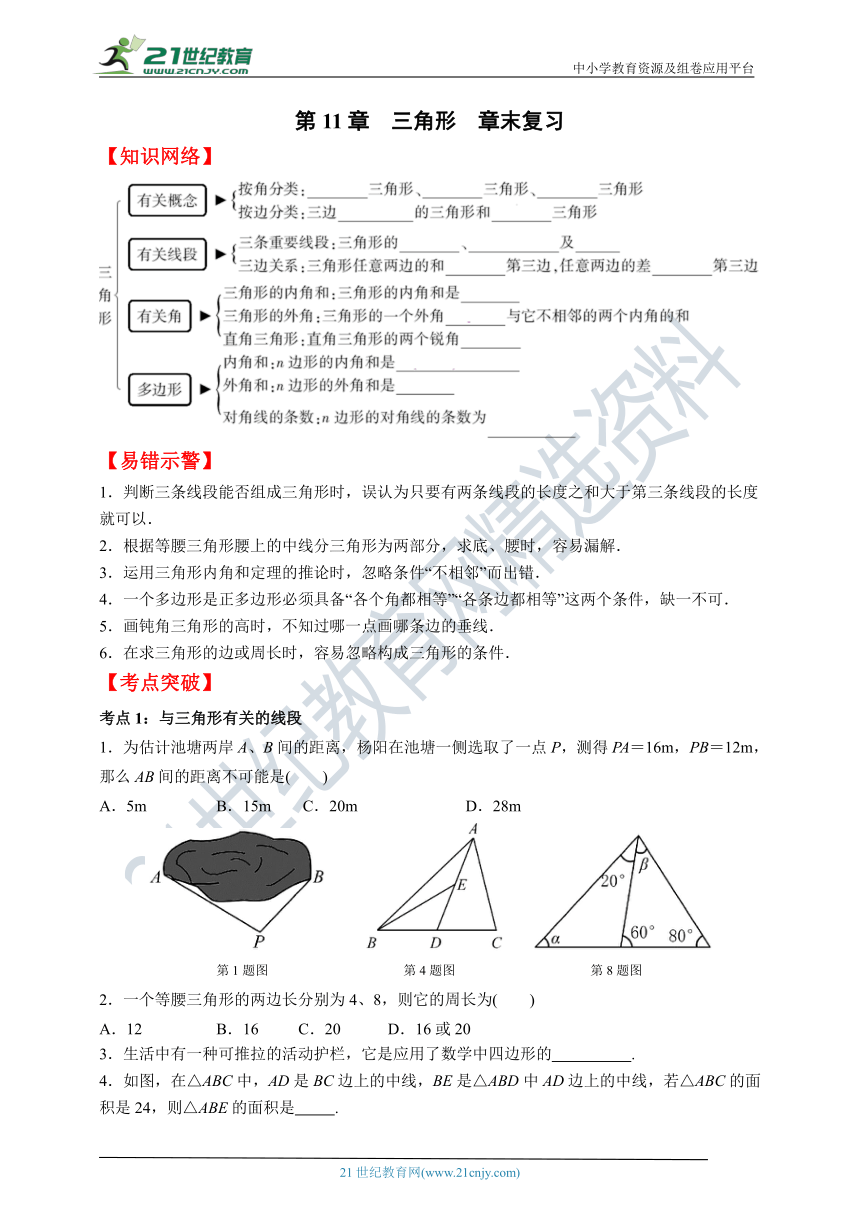
【知识网络】
【易错示警】
1.判断三条线段能否组成三角形时,误认为只要有两条线段的长度之和大于第三条线段的长度就可以.
2.根据等腰三角形腰上的中线分三角形为两部分,求底、腰时,容易漏解.
3.运用三角形内角和定理的推论时,忽略条件“不相邻”而出错.
4.一个多边形是正多边形必须具备“各个角都相等”“各条边都相等”这两个条件,缺一不可.
5.画钝角三角形的高时,不知过哪一点画哪条边的垂线.
6.在求三角形的边或周长时,容易忽略构成三角形的条件.
【考点突破】
考点1:与三角形有关的线段
1.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
A.5m B.15m C.20m D.28m
第1题图 第4题图 第8题图
2.一个等腰三角形的两边长分别为4、8,则它的周长为( )
A.12 B.16 C.20 D.16或20
3.生活中有一种可推拉的活动护栏,它是应用了数学中四边形的 .
4.如图,在△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是 .
5.有两根长度分别为2cm和5cm的木棒.
(1)用长度为3cm的木棒与它们能摆成三角形吗?为什么?
(2)用长度为1cm的木棒呢?
(3)要能摆成三角形,第三边能用的木棒的长度范围是多少?
6.如图所示:已知△ABC.
(1)作出△ABC的三条高线;
(2)如果△ABC的三边分别为AB=6,BC=5,AC=4,那么(1)中的三条高线的比是多少?
考点2:与三角形有关的角
7.一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
8.如图所示,图中∠α、∠β的度数分别是( C )
A.30°,50° B.40°,80° C.40°,40° D.60°,40°
9.将一副三角板如图叠放,则图中∠α的度数为 .
10.已知,在△ABC中,AD是BC边上的高线,且∠ABC=26°,∠ACD=55°,则∠BAC= .
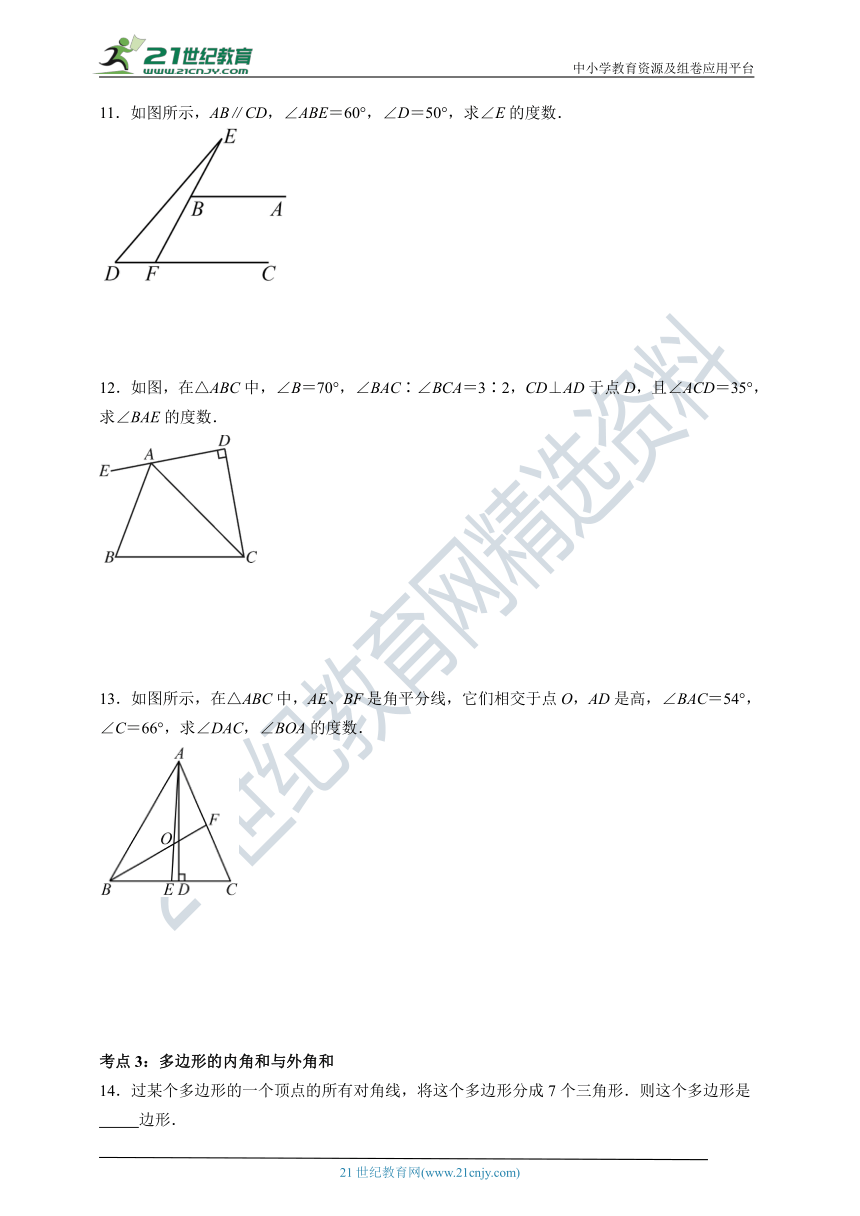
11.如图所示,AB∥CD,∠ABE=60°,∠D=50°,求∠E的度数.
12.如图,在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,CD⊥AD于点D,且∠ACD=35°,求∠BAE的度数.
13.如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC,∠BOA的度数.
考点3:多边形的内角和与外角和
14.过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形.则这个多边形是
边形.
15.已知多边形的内角和与某一个外角的度数之和为2550°,求这个多边形的边数.
16.如图,在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
【综合练习】
1.下列说法正确的是( )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
2.下列各组数可能是一个三角形的边长的是( )
A.1、2、4 B.4、5、9 C.4、6、8 D.5、5、11
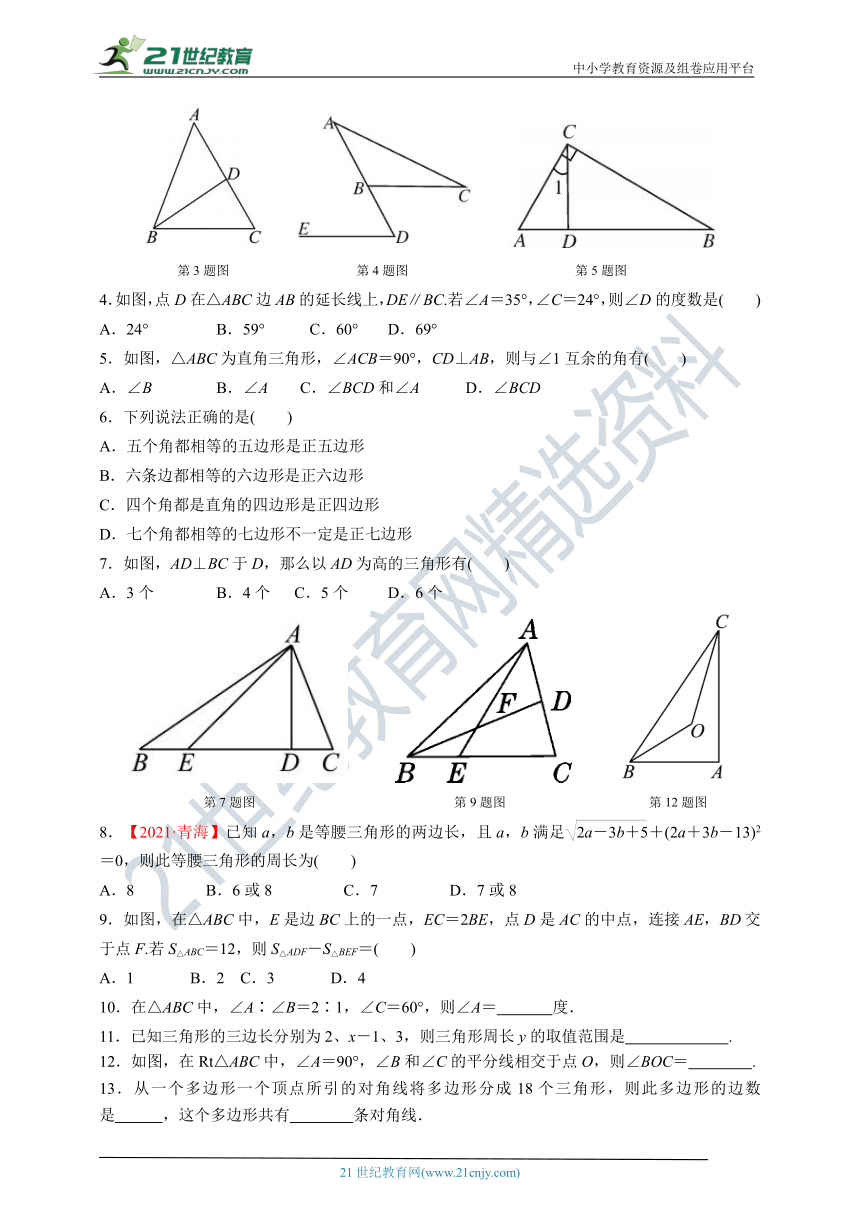
3.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
第3题图 第4题图 第5题图
4.如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
5.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB,则与∠1互余的角有( )
A.∠B B.∠A C.∠BCD和∠A D.∠BCD
6.下列说法正确的是( )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正四边形
D.七个角都相等的七边形不一定是正七边形
7.如图,AD⊥BC于D,那么以AD为高的三角形有( )
A.3个 B.4个 C.5个 D.6个
第7题图 第9题图 第12题图
8.【2021·青海】已知a,b是等腰三角形的两边长,且a,b满足+(2a+3b-13)2=0,则此等腰三角形的周长为( )
A.8 B.6或8 C.7 D.7或8
9.如图,在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F.若S△ABC=12,则S△ADF-S△BEF=( )
A.1 B.2 C.3 D.4
10.在△ABC中,∠A∶∠B=2∶1,∠C=60°,则∠A= 度.
11.已知三角形的三边长分别为2、x-1、3,则三角形周长y的取值范围是 .
12.如图,在Rt△ABC中,∠A=90°,∠B和∠C的平分线相交于点O,则∠BOC= .
13.从一个多边形一个顶点所引的对角线将多边形分成18个三角形,则此多边形的边数是 ,这个多边形共有 条对角线.
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=________.
15.画出下面三角形的高AD.
16.如图所示,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
17.等腰三角形的两边长a,b满足|a-4|+(b-9)2=0,求这个等腰三角形的周长.
18.已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
19.如图,在等边三角形ABC中,BD为AC边上的高,G为△ABC内任意一点,GF⊥AB,GE⊥AC,GH⊥BC,垂足分别为F,E,H.求证:GF+GE+GH=BD.
20.如图,在△ABC中,BD、CD是内角平分线,BP、CP是∠ABC、∠ACB的外角平分线,分别交于D、P.
(1)若∠A=30°,求∠BDC、∠BPC的度数;
(2)若∠A=m°,求∠BDC、∠BPC的度数(直接写出结果,不必说明理由);
(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由;若无影响,直接求出其值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【知识网络】
【易错示警】
1.判断三条线段能否组成三角形时,误认为只要有两条线段的长度之和大于第三条线段的长度就可以.
2.根据等腰三角形腰上的中线分三角形为两部分,求底、腰时,容易漏解.
3.运用三角形内角和定理的推论时,忽略条件“不相邻”而出错.
4.一个多边形是正多边形必须具备“各个角都相等”“各条边都相等”这两个条件,缺一不可.
5.画钝角三角形的高时,不知过哪一点画哪条边的垂线.
6.在求三角形的边或周长时,容易忽略构成三角形的条件.
【考点突破】
考点1:与三角形有关的线段
1.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( D )
A.5m B.15m C.20m D.28m
第1题图 第4题图 第8题图
2.一个等腰三角形的两边长分别为4、8,则它的周长为( C )
A.12 B.16 C.20 D.16或20
3.生活中有一种可推拉的活动护栏,它是应用了数学中四边形的 .
【答案】不稳定性
4.如图,在△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是 .
【答案】6
5.有两根长度分别为2cm和5cm的木棒.
(1)用长度为3cm的木棒与它们能摆成三角形吗?为什么?
(2)用长度为1cm的木棒呢?
(3)要能摆成三角形,第三边能用的木棒的长度范围是多少?
解:(1)不能,由于2+3=5,所以它们不能摆成三角形;
(2)用长度为1cm的木棒时,由于1+2=3<5,所以它们也不能摆成三角形;
(3)设第三根木棒长为xcm,因为2+5=7,所以第三根木棒的长度必须小于7cm;又因为5-2=3,所以第三根木棒的长度必须大于3cm,所以3<x<7.即要能摆成三角形,第三边能用的木棒的长度范围是大于3cm且小于7cm.
6.如图所示:已知△ABC.
(1)作出△ABC的三条高线;
(2)如果△ABC的三边分别为AB=6,BC=5,AC=4,那么(1)中的三条高线的比是多少?
解(1)如图所示:;
(2)设AB、BC、AC边上的高为h1、h2、h3,根据题意,得6h1=5h2=4h3,所以h1∶h2∶h3=∶∶=10∶12∶15.
考点2:与三角形有关的角
7.一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
8.如图所示,图中∠α、∠β的度数分别是( C )
A.30°,50° B.40°,80° C.40°,40° D.60°,40°
9.将一副三角板如图叠放,则图中∠α的度数为 .
【答案】15°
10.已知,在△ABC中,AD是BC边上的高线,且∠ABC=26°,∠ACD=55°,则∠BAC= .
【答案】99°或29°
11.如图所示,AB∥CD,∠ABE=60°,∠D=50°,求∠E的度数.
解:∵AB∥CD,∠ABE=60°,∴∠EFC=∠ABE=60°.又∵∠D=50°,∠D+∠E=∠EFC,∴∠E=∠CFE-∠D=60°-50°=10°.
12.如图,在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,CD⊥AD于点D,且∠ACD=35°,求∠BAE的度数.
【解析】∠BAE不是三角形的内角,但与∠BAD互为邻补角,故可转化求∠BAD的度数,即求∠BAC和∠CAD的度数;而∠BAC和∠CAD分别是△BAC和△ACD的内角,结合题意,根据三角形的内角和及直角三角形的性质,问题得解.
【解答】在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,∴可设∠BAC=3x°,则∠BCA=2x°.∵∠B+∠BAC+∠BCA=180°,∴70°+3x°+2x°=180°,解得x=22.∴∠BAC=3×22°=66°.又CD⊥AD,∴∠D=90°.∴∠CAD+∠ACD=90°,∴∠CAD=90°-∠ACD=90°-35°=55°.∵∠DAE是平角,∴∠BAE=180°-∠BAC-∠CAD=180°-66°-55°=59°.
13.如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC,∠BOA的度数.
解:∵AD是高,∴∠ADC=90°,∵∠C=66°∴∠DAC=180°-90°-66°=24°.∵∠BAC=54°,∠C=66°,AE是角平分线,∴∠BAO=27°,∠ABC=60°.∵BF是∠ABC的角平分线,∴∠ABO=30°,∴∠BOA=180°-∠BAO-∠ABO=123°.
考点3:多边形的内角和与外角和
14.过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形.则这个多边形是
边形.
【答案】九
15.已知多边形的内角和与某一个外角的度数之和为2550°,求这个多边形的边数.
解:设多边形的边数为n,这个外角为x,则0°<x<180°.根据题意,得(n-2)×180°+x=2550°.解得x=2910°-180°n.∵0°<x<180°,∴0°<2910°-180°n<180°,解得15<n<16,∴n=16.即这个多边形的边数为16.
16.如图,在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
解:(1)在四边形ABCD中,∠A+∠B+∠C+∠D=360°, ∵∠A=140°,∠D=80°,∠B=∠C,∴140°+80°+2∠C=360°,∴∠C=70°;
(2)∵∠A=140°,∠D=80°,BE∥AD,∴∠ABE=180°-∠A=180°-140°=40°,∠BED=180°-∠D=180°-80°=100°.又∵BE是∠ABC的角平分线,∴∠EBC=∠ABE=40°.∴∠C=∠BED-∠EBC=100°-40°=60°;
(3)∵∠A=140°,∠D=80°,∠ABC+∠BCD=360°-(∠A+∠D)=360°-(140°+80°)=140°,又∵BE、CE分别是∠ABC、∠BCD的角平分线,∴∠EBC+∠ECB=∠ABC+∠BCD=(∠ABC+∠BCD)=×140°=70°.∴在△BEC中,∠BEC=180°-(∠EBC+∠ECB)=180°-70°=110°.
【综合练习】
1.下列说法正确的是( C )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
2.下列各组数可能是一个三角形的边长的是( C )
A.1、2、4 B.4、5、9 C.4、6、8 D.5、5、11
3.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( A )
A.85° B.80° C.75° D.70°
第3题图 第4题图 第5题图
4.如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( B )
A.24° B.59° C.60° D.69°
5.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB,则与∠1互余的角有( C )
A.∠B B.∠A C.∠BCD和∠A D.∠BCD
6.下列说法正确的是( D )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正四边形
D.七个角都相等的七边形不一定是正七边形
7.如图,AD⊥BC于D,那么以AD为高的三角形有( D )
A.3个 B.4个 C.5个 D.6个
第7题图 第9题图 第12题图
8.【2021·青海】已知a,b是等腰三角形的两边长,且a,b满足+(2a+3b-13)2=0,则此等腰三角形的周长为( D )
A.8 B.6或8 C.7 D.7或8
【解析】由题意,得解得
当b为底边长时,三角形的三边长为2,2,3,周长为7;
当a为底边长时,三角形的三边长为2,3,3,周长为8,
∴等腰三角形的周长为7或8.
9.如图,在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F.若S△ABC=12,则S△ADF-S△BEF=( B )
A.1 B.2 C.3 D.4
【解析】∵EC=2BE,点D是AC的中点,
∴S△ABE=S△ABC=×12=4,S△ABD=S△ABC=×12=6.
∴S△ADF-S△BEF=(S△ADF+S△ABF)-(S△BEF+S△ABF)=S△ABD-S△ABE=6-4=2,故选B.
10.在△ABC中,∠A∶∠B=2∶1,∠C=60°,则∠A= 度.
【答案】80
11.已知三角形的三边长分别为2、x-1、3,则三角形周长y的取值范围是 .
【答案】6<y<10
12.如图,在Rt△ABC中,∠A=90°,∠B和∠C的平分线相交于点O,则∠BOC= .
【答案】135°
13.从一个多边形一个顶点所引的对角线将多边形分成18个三角形,则此多边形的边数是 ,这个多边形共有 条对角线.
【答案】20 170
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=________.
【答案】540°
15.画出下面三角形的高AD.
解:如图所示,AD即为所作高.
16.如图所示,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
解:(1)∵AD⊥BC于D,∴∠ADB=∠ADC=90°.∵∠ABC=40°,∠C=60°,∴∠BAD=50°,∠CAD=30°.∴∠BAC=50°+30°=80°,∵AE是∠BAC的平分线,∴∠BAE=40°.∴∠DAE=50°-40°=10°;
(2)AD是△ABE、△ABD、△ABC、△AED、△AEC、△ADC的高.
17.等腰三角形的两边长a,b满足|a-4|+(b-9)2=0,求这个等腰三角形的周长.
解:∵|a-4|+(b-9)2=0,
∴|a-4|=0,(b-9)2=0.∴a=4,b=9.
若腰长为4,则4+4<9,不能构成三角形;
若腰长为9,则9+4>9,能构成三角形.
故这个等腰三角形的周长为9+9+4=22.
18.已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
解:(1)甲对,乙不对.理由:∵θ=360°,∴(n-2)·180°=360°,解得n=4.∵θ=630°,∴(n-2)·180°=630°,解得n=.∵n为整数,∴θ不能取630°;
(2)依题意,得(n-2)·180°+360°=(n+x-2)·180°,解得x=2.
19.如图,在等边三角形ABC中,BD为AC边上的高,G为△ABC内任意一点,GF⊥AB,GE⊥AC,GH⊥BC,垂足分别为F,E,H.求证:GF+GE+GH=BD.
证明:如图,连接GA,GB,GC.
∵BD是AC边上的高,∴S△ABC=AC·BD.
∵GF⊥AB,GE⊥AC,GH⊥BC,
∴S△ABC=S△ABG+S△BCG+S△ACG
=AB·GF+BC·GH+AC·GE.
∵△ABC为等边三角形,∴AB=BC=AC,
∴S△ABC=AC·(GF+GE+GH)=AC·BD.
∴GF+GE+GH=BD.
20.如图,在△ABC中,BD、CD是内角平分线,BP、CP是∠ABC、∠ACB的外角平分线,分别交于D、P.
(1)若∠A=30°,求∠BDC、∠BPC的度数;
(2)若∠A=m°,求∠BDC、∠BPC的度数(直接写出结果,不必说明理由);
(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由;若无影响,直接求出其值.
解:(1)∵∠A=30°,∴∠ABC+∠ACB=150°,∵BD、CD分别平分∠ABC、∠ACB,∴∠DBC+∠DCB=75°,∴∠BDC=180°-75°=105°.∵∠EBC+∠FCB=360°-150°=210°,又∵BP、CP分别平分∠EBC、∠FCB,∴∠PBC+∠PCB=105°,∴∠BPC=75°;
(2)∠BDC=90°+m°,∠BPC=90°-m°;
(3)无影响,∠D+∠P=180°.
【知识网络】
【易错示警】
1.判断三条线段能否组成三角形时,误认为只要有两条线段的长度之和大于第三条线段的长度就可以.
2.根据等腰三角形腰上的中线分三角形为两部分,求底、腰时,容易漏解.
3.运用三角形内角和定理的推论时,忽略条件“不相邻”而出错.
4.一个多边形是正多边形必须具备“各个角都相等”“各条边都相等”这两个条件,缺一不可.
5.画钝角三角形的高时,不知过哪一点画哪条边的垂线.
6.在求三角形的边或周长时,容易忽略构成三角形的条件.
【考点突破】
考点1:与三角形有关的线段
1.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
A.5m B.15m C.20m D.28m
第1题图 第4题图 第8题图
2.一个等腰三角形的两边长分别为4、8,则它的周长为( )
A.12 B.16 C.20 D.16或20
3.生活中有一种可推拉的活动护栏,它是应用了数学中四边形的 .
4.如图,在△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是 .
5.有两根长度分别为2cm和5cm的木棒.
(1)用长度为3cm的木棒与它们能摆成三角形吗?为什么?
(2)用长度为1cm的木棒呢?
(3)要能摆成三角形,第三边能用的木棒的长度范围是多少?
6.如图所示:已知△ABC.
(1)作出△ABC的三条高线;
(2)如果△ABC的三边分别为AB=6,BC=5,AC=4,那么(1)中的三条高线的比是多少?
考点2:与三角形有关的角
7.一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
8.如图所示,图中∠α、∠β的度数分别是( C )
A.30°,50° B.40°,80° C.40°,40° D.60°,40°
9.将一副三角板如图叠放,则图中∠α的度数为 .
10.已知,在△ABC中,AD是BC边上的高线,且∠ABC=26°,∠ACD=55°,则∠BAC= .
11.如图所示,AB∥CD,∠ABE=60°,∠D=50°,求∠E的度数.
12.如图,在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,CD⊥AD于点D,且∠ACD=35°,求∠BAE的度数.
13.如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC,∠BOA的度数.
考点3:多边形的内角和与外角和
14.过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形.则这个多边形是
边形.
15.已知多边形的内角和与某一个外角的度数之和为2550°,求这个多边形的边数.
16.如图,在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
【综合练习】
1.下列说法正确的是( )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
2.下列各组数可能是一个三角形的边长的是( )
A.1、2、4 B.4、5、9 C.4、6、8 D.5、5、11
3.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
第3题图 第4题图 第5题图
4.如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
5.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB,则与∠1互余的角有( )
A.∠B B.∠A C.∠BCD和∠A D.∠BCD
6.下列说法正确的是( )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正四边形
D.七个角都相等的七边形不一定是正七边形
7.如图,AD⊥BC于D,那么以AD为高的三角形有( )
A.3个 B.4个 C.5个 D.6个
第7题图 第9题图 第12题图
8.【2021·青海】已知a,b是等腰三角形的两边长,且a,b满足+(2a+3b-13)2=0,则此等腰三角形的周长为( )
A.8 B.6或8 C.7 D.7或8
9.如图,在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F.若S△ABC=12,则S△ADF-S△BEF=( )
A.1 B.2 C.3 D.4
10.在△ABC中,∠A∶∠B=2∶1,∠C=60°,则∠A= 度.
11.已知三角形的三边长分别为2、x-1、3,则三角形周长y的取值范围是 .
12.如图,在Rt△ABC中,∠A=90°,∠B和∠C的平分线相交于点O,则∠BOC= .
13.从一个多边形一个顶点所引的对角线将多边形分成18个三角形,则此多边形的边数是 ,这个多边形共有 条对角线.
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=________.
15.画出下面三角形的高AD.
16.如图所示,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
17.等腰三角形的两边长a,b满足|a-4|+(b-9)2=0,求这个等腰三角形的周长.
18.已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
19.如图,在等边三角形ABC中,BD为AC边上的高,G为△ABC内任意一点,GF⊥AB,GE⊥AC,GH⊥BC,垂足分别为F,E,H.求证:GF+GE+GH=BD.
20.如图,在△ABC中,BD、CD是内角平分线,BP、CP是∠ABC、∠ACB的外角平分线,分别交于D、P.
(1)若∠A=30°,求∠BDC、∠BPC的度数;
(2)若∠A=m°,求∠BDC、∠BPC的度数(直接写出结果,不必说明理由);
(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由;若无影响,直接求出其值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【知识网络】
【易错示警】
1.判断三条线段能否组成三角形时,误认为只要有两条线段的长度之和大于第三条线段的长度就可以.
2.根据等腰三角形腰上的中线分三角形为两部分,求底、腰时,容易漏解.
3.运用三角形内角和定理的推论时,忽略条件“不相邻”而出错.
4.一个多边形是正多边形必须具备“各个角都相等”“各条边都相等”这两个条件,缺一不可.
5.画钝角三角形的高时,不知过哪一点画哪条边的垂线.
6.在求三角形的边或周长时,容易忽略构成三角形的条件.
【考点突破】
考点1:与三角形有关的线段
1.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( D )
A.5m B.15m C.20m D.28m
第1题图 第4题图 第8题图
2.一个等腰三角形的两边长分别为4、8,则它的周长为( C )
A.12 B.16 C.20 D.16或20
3.生活中有一种可推拉的活动护栏,它是应用了数学中四边形的 .
【答案】不稳定性
4.如图,在△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是 .
【答案】6
5.有两根长度分别为2cm和5cm的木棒.
(1)用长度为3cm的木棒与它们能摆成三角形吗?为什么?
(2)用长度为1cm的木棒呢?
(3)要能摆成三角形,第三边能用的木棒的长度范围是多少?
解:(1)不能,由于2+3=5,所以它们不能摆成三角形;
(2)用长度为1cm的木棒时,由于1+2=3<5,所以它们也不能摆成三角形;
(3)设第三根木棒长为xcm,因为2+5=7,所以第三根木棒的长度必须小于7cm;又因为5-2=3,所以第三根木棒的长度必须大于3cm,所以3<x<7.即要能摆成三角形,第三边能用的木棒的长度范围是大于3cm且小于7cm.
6.如图所示:已知△ABC.
(1)作出△ABC的三条高线;
(2)如果△ABC的三边分别为AB=6,BC=5,AC=4,那么(1)中的三条高线的比是多少?
解(1)如图所示:;
(2)设AB、BC、AC边上的高为h1、h2、h3,根据题意,得6h1=5h2=4h3,所以h1∶h2∶h3=∶∶=10∶12∶15.
考点2:与三角形有关的角
7.一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
8.如图所示,图中∠α、∠β的度数分别是( C )
A.30°,50° B.40°,80° C.40°,40° D.60°,40°
9.将一副三角板如图叠放,则图中∠α的度数为 .
【答案】15°
10.已知,在△ABC中,AD是BC边上的高线,且∠ABC=26°,∠ACD=55°,则∠BAC= .
【答案】99°或29°
11.如图所示,AB∥CD,∠ABE=60°,∠D=50°,求∠E的度数.
解:∵AB∥CD,∠ABE=60°,∴∠EFC=∠ABE=60°.又∵∠D=50°,∠D+∠E=∠EFC,∴∠E=∠CFE-∠D=60°-50°=10°.
12.如图,在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,CD⊥AD于点D,且∠ACD=35°,求∠BAE的度数.
【解析】∠BAE不是三角形的内角,但与∠BAD互为邻补角,故可转化求∠BAD的度数,即求∠BAC和∠CAD的度数;而∠BAC和∠CAD分别是△BAC和△ACD的内角,结合题意,根据三角形的内角和及直角三角形的性质,问题得解.
【解答】在△ABC中,∠B=70°,∠BAC∶∠BCA=3∶2,∴可设∠BAC=3x°,则∠BCA=2x°.∵∠B+∠BAC+∠BCA=180°,∴70°+3x°+2x°=180°,解得x=22.∴∠BAC=3×22°=66°.又CD⊥AD,∴∠D=90°.∴∠CAD+∠ACD=90°,∴∠CAD=90°-∠ACD=90°-35°=55°.∵∠DAE是平角,∴∠BAE=180°-∠BAC-∠CAD=180°-66°-55°=59°.
13.如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC,∠BOA的度数.
解:∵AD是高,∴∠ADC=90°,∵∠C=66°∴∠DAC=180°-90°-66°=24°.∵∠BAC=54°,∠C=66°,AE是角平分线,∴∠BAO=27°,∠ABC=60°.∵BF是∠ABC的角平分线,∴∠ABO=30°,∴∠BOA=180°-∠BAO-∠ABO=123°.
考点3:多边形的内角和与外角和
14.过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形.则这个多边形是
边形.
【答案】九
15.已知多边形的内角和与某一个外角的度数之和为2550°,求这个多边形的边数.
解:设多边形的边数为n,这个外角为x,则0°<x<180°.根据题意,得(n-2)×180°+x=2550°.解得x=2910°-180°n.∵0°<x<180°,∴0°<2910°-180°n<180°,解得15<n<16,∴n=16.即这个多边形的边数为16.
16.如图,在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
解:(1)在四边形ABCD中,∠A+∠B+∠C+∠D=360°, ∵∠A=140°,∠D=80°,∠B=∠C,∴140°+80°+2∠C=360°,∴∠C=70°;
(2)∵∠A=140°,∠D=80°,BE∥AD,∴∠ABE=180°-∠A=180°-140°=40°,∠BED=180°-∠D=180°-80°=100°.又∵BE是∠ABC的角平分线,∴∠EBC=∠ABE=40°.∴∠C=∠BED-∠EBC=100°-40°=60°;
(3)∵∠A=140°,∠D=80°,∠ABC+∠BCD=360°-(∠A+∠D)=360°-(140°+80°)=140°,又∵BE、CE分别是∠ABC、∠BCD的角平分线,∴∠EBC+∠ECB=∠ABC+∠BCD=(∠ABC+∠BCD)=×140°=70°.∴在△BEC中,∠BEC=180°-(∠EBC+∠ECB)=180°-70°=110°.
【综合练习】
1.下列说法正确的是( C )
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
2.下列各组数可能是一个三角形的边长的是( C )
A.1、2、4 B.4、5、9 C.4、6、8 D.5、5、11
3.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( A )
A.85° B.80° C.75° D.70°
第3题图 第4题图 第5题图
4.如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( B )
A.24° B.59° C.60° D.69°
5.如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB,则与∠1互余的角有( C )
A.∠B B.∠A C.∠BCD和∠A D.∠BCD
6.下列说法正确的是( D )
A.五个角都相等的五边形是正五边形
B.六条边都相等的六边形是正六边形
C.四个角都是直角的四边形是正四边形
D.七个角都相等的七边形不一定是正七边形
7.如图,AD⊥BC于D,那么以AD为高的三角形有( D )
A.3个 B.4个 C.5个 D.6个
第7题图 第9题图 第12题图
8.【2021·青海】已知a,b是等腰三角形的两边长,且a,b满足+(2a+3b-13)2=0,则此等腰三角形的周长为( D )
A.8 B.6或8 C.7 D.7或8
【解析】由题意,得解得
当b为底边长时,三角形的三边长为2,2,3,周长为7;
当a为底边长时,三角形的三边长为2,3,3,周长为8,
∴等腰三角形的周长为7或8.
9.如图,在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F.若S△ABC=12,则S△ADF-S△BEF=( B )
A.1 B.2 C.3 D.4
【解析】∵EC=2BE,点D是AC的中点,
∴S△ABE=S△ABC=×12=4,S△ABD=S△ABC=×12=6.
∴S△ADF-S△BEF=(S△ADF+S△ABF)-(S△BEF+S△ABF)=S△ABD-S△ABE=6-4=2,故选B.
10.在△ABC中,∠A∶∠B=2∶1,∠C=60°,则∠A= 度.
【答案】80
11.已知三角形的三边长分别为2、x-1、3,则三角形周长y的取值范围是 .
【答案】6<y<10
12.如图,在Rt△ABC中,∠A=90°,∠B和∠C的平分线相交于点O,则∠BOC= .
【答案】135°
13.从一个多边形一个顶点所引的对角线将多边形分成18个三角形,则此多边形的边数是 ,这个多边形共有 条对角线.
【答案】20 170
14.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=________.
【答案】540°
15.画出下面三角形的高AD.
解:如图所示,AD即为所作高.
16.如图所示,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
解:(1)∵AD⊥BC于D,∴∠ADB=∠ADC=90°.∵∠ABC=40°,∠C=60°,∴∠BAD=50°,∠CAD=30°.∴∠BAC=50°+30°=80°,∵AE是∠BAC的平分线,∴∠BAE=40°.∴∠DAE=50°-40°=10°;
(2)AD是△ABE、△ABD、△ABC、△AED、△AEC、△ADC的高.
17.等腰三角形的两边长a,b满足|a-4|+(b-9)2=0,求这个等腰三角形的周长.
解:∵|a-4|+(b-9)2=0,
∴|a-4|=0,(b-9)2=0.∴a=4,b=9.
若腰长为4,则4+4<9,不能构成三角形;
若腰长为9,则9+4>9,能构成三角形.
故这个等腰三角形的周长为9+9+4=22.
18.已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,请说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
解:(1)甲对,乙不对.理由:∵θ=360°,∴(n-2)·180°=360°,解得n=4.∵θ=630°,∴(n-2)·180°=630°,解得n=.∵n为整数,∴θ不能取630°;
(2)依题意,得(n-2)·180°+360°=(n+x-2)·180°,解得x=2.
19.如图,在等边三角形ABC中,BD为AC边上的高,G为△ABC内任意一点,GF⊥AB,GE⊥AC,GH⊥BC,垂足分别为F,E,H.求证:GF+GE+GH=BD.
证明:如图,连接GA,GB,GC.
∵BD是AC边上的高,∴S△ABC=AC·BD.
∵GF⊥AB,GE⊥AC,GH⊥BC,
∴S△ABC=S△ABG+S△BCG+S△ACG
=AB·GF+BC·GH+AC·GE.
∵△ABC为等边三角形,∴AB=BC=AC,
∴S△ABC=AC·(GF+GE+GH)=AC·BD.
∴GF+GE+GH=BD.
20.如图,在△ABC中,BD、CD是内角平分线,BP、CP是∠ABC、∠ACB的外角平分线,分别交于D、P.
(1)若∠A=30°,求∠BDC、∠BPC的度数;
(2)若∠A=m°,求∠BDC、∠BPC的度数(直接写出结果,不必说明理由);
(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由;若无影响,直接求出其值.
解:(1)∵∠A=30°,∴∠ABC+∠ACB=150°,∵BD、CD分别平分∠ABC、∠ACB,∴∠DBC+∠DCB=75°,∴∠BDC=180°-75°=105°.∵∠EBC+∠FCB=360°-150°=210°,又∵BP、CP分别平分∠EBC、∠FCB,∴∠PBC+∠PCB=105°,∴∠BPC=75°;
(2)∠BDC=90°+m°,∠BPC=90°-m°;
(3)无影响,∠D+∠P=180°.
