不等式的性质[下学期]

课件18张PPT。初中七年级数学好好学习
天天向上不等式与不等式组
－－－－－9.1.2.不等式的性质问题1：什么是不等式?
含有不等号的式子叫不等式。一元一次不等式是只含有一个未知数，且
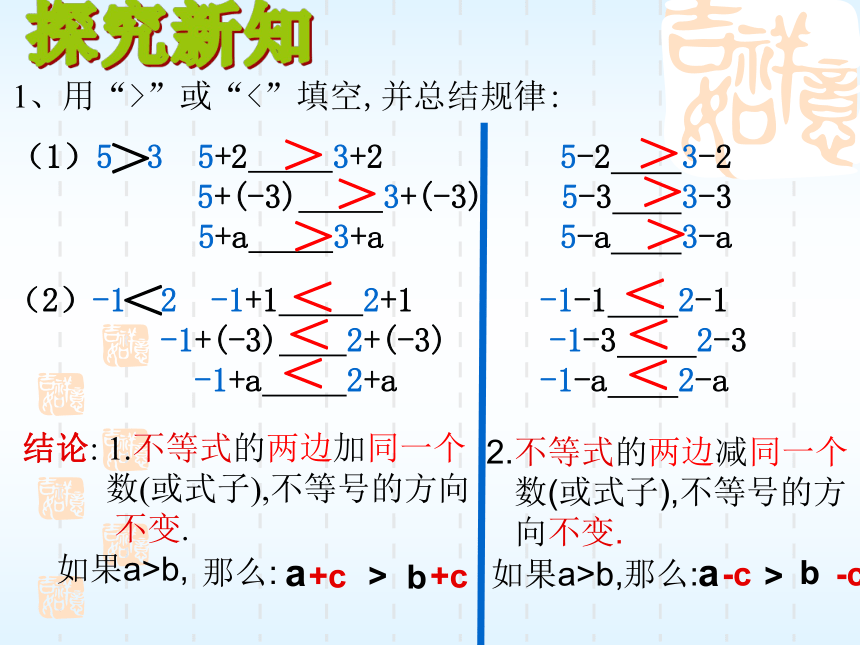
未知数的次数是1 的不等式。注:不等号包括”>”,”<”,” ”,”≥”,”≤”.问题2： 什么是一元一次不等式？探究新知1、用“>”或“<”填空,并总结规律:
（1）5 3 5+2 3+2 5-2 3-2
5+(-3) 3+(-3) 5-3 3-3
5+a 3+a 5-a 3-a
＜＜＞＞＞＞＞＞＞（2）-1 2 -1+1 2+1 -1-1 2-1
-1+(-3) 2+(-3) -1-3 2-3
-1+a 2+a -1-a 2-a
＜＜＜＜结论: 1.不等式的两边加同一个
数(或式子),不等号的方向
不变.＜2.不等式的两边减同一个
数(或式子),不等号的方
向不变.+c +cab>如果a>b,那么:ab>-c -c如果a>b,那么:不等式性质1：不等式的两边加上（或减去）同一个数
（或式子），不等号的方向不变。ab>练习：一、判断下列说法是否正确，对的打勾，错的打叉
并说明原因。（1）若1+2<4，则1+2 <4
（2）若x>y,则x >y
（3）若x-5>y-5, 则x>y
（4）若xy+5
（5）若2x>x+1, 则2x >x+1（ ）（ ）（ ）（ ）（ ）√√√X+3+3-a-a两边同时加上5+5-x-x如果a b,那么:><<√(1)如果4-2>1，那么4-2+3____ -1+3
二、填空(3)如果a-1>b，那么a-1 >b______;(2)如果3x+5<8,那么3x<8______; +1(4)如果5x>-2x+7，那么5x+___ >7;-5+12x>结论: 1.不等式的两边乘以同一个
正数，不等号的方向不变。2.不等式的两边除以同一个
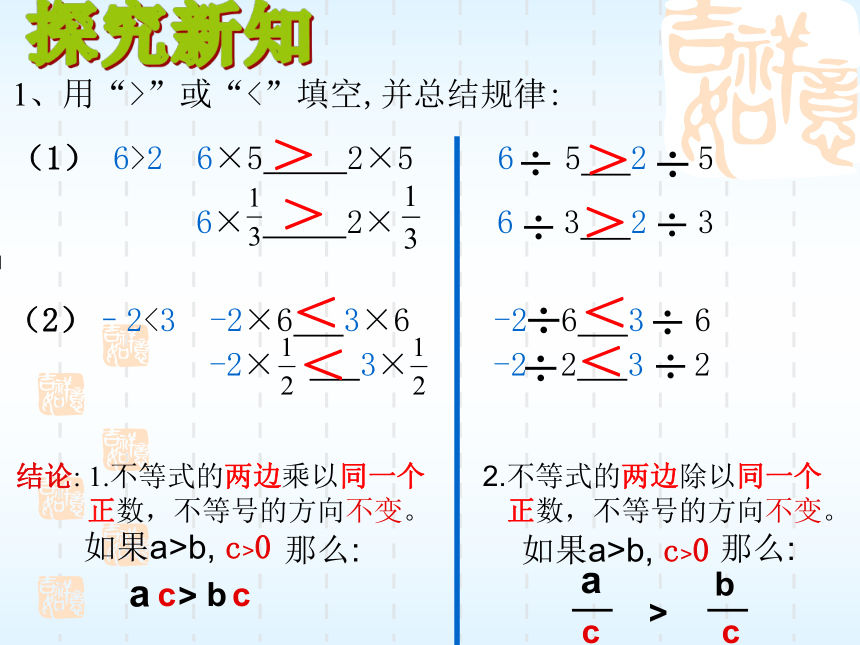
正数，不等号的方向不变。abc c>a b>c c探究新知1、用“>”或“<”填空,并总结规律:
（1） 6>2 6×5 2×5 6 5 2 5
6× 2× 6 3 2 3
（2）–2<3 -2×6 3×6 -2 6 3 6
-2× 3× -2 2 3 2

＞＞＞＞＜＜＜＜如果a>b, c>0那么:如果a>b, c>0那么: 如果a>b,c >0 那么ac>bc；如果a>b,c >0，那么－>－.不等式的性质2: 不等式两边乘以(或除以)同一个正数，
不等号的方向不变。ccab练习：一、判断下列说法是否正确，对的打勾，错的打叉
并说明原因。（1）若a>b，则 3a<3 b
（2）若x>y, 则
（3）若 , 则
（4）若x0(1)如果5x>15，那么5x 5>15 　　 ，(2)如果 ，那么 ,二、填空53结论: 1.不等式的两边乘以同一个
负数，不等号的方向改变。2.不等式的两边除以同一个
负数，不等号的方向改变。abc c”或“<”填空,并总结规律:
（1） 6>2 6×(-5) 2×(-5) 6 (-5)__ 2 (-5)
6× 2× 6 (-2) 2 (-2)
（2） 2<3 2×(-6) 3×(-6) 2 (-6) 3 (-6)
2× 3× 2 (-2)___3 (-2)
＞＞＞＜＜＞＜＜如果a>b, c<0那么:如果a>b, c<0那么: 如果a>b,c <0 那么acb,c <0，那么－<－.不等式的性质3: 不等式两边乘以(或除以)同一个负数，
不等号的方向改变。ccab练习：一、判断下列说法是否正确，对的打勾，错的打叉
并说明原因。（1）若a>b，则 a<-3 b
（2）若x>y, 则
（3）若 ,则
（4）若 ,则（ ）（ ）（ ）（ ）√√√-3(1)如果-5x>15，那么-5x (-5) < 15 　　 ，(2)如果 ，那么 ,二、填空(-5)(-3)X一、选择1.下列不等式变形符合等式性质的是（ ）
A.如果2x-1>3,那么2x>3-1 B.如果-2x<5,那么x<5+2
C.如果 ，那么x>-3 D.如果x>y,那么x-5>y+52.下列说法正确的是（ ）
A.不等式两边各加上一个式子，不等号方向不变
B.不等式两边各乘以一个数，不等号方向不变
C.不等式两边都除以同一个数，不等号的方向不变
D.不等式两边各减去一个相同的数，不等号的方向不变 CD>>><<二.小结：不等式的性质1：不等式的两边加上（或减去）同一个数（或式子），
不等号的方向不变。 如果a>b,c >0 ,那么ac>bc；如果a>b,c >0,那么－>－.不等式的性质2: 不等式两边乘以(或除以)同一个正数，
不等号的方向不变。ccabab>如果a b,那么:>作业：P133 练习1,2 如果a>b,c <0 那么acb,c <0，那么－<－.不等式的性质3: 不等式两边乘以(或除以)同一个负数，
不等号的方向改变。ccababa>babcca>ba b+c+ca b-c-c>>aaabbba>b(c>0)a bcca bcc>>