不等式的性质[下学期]

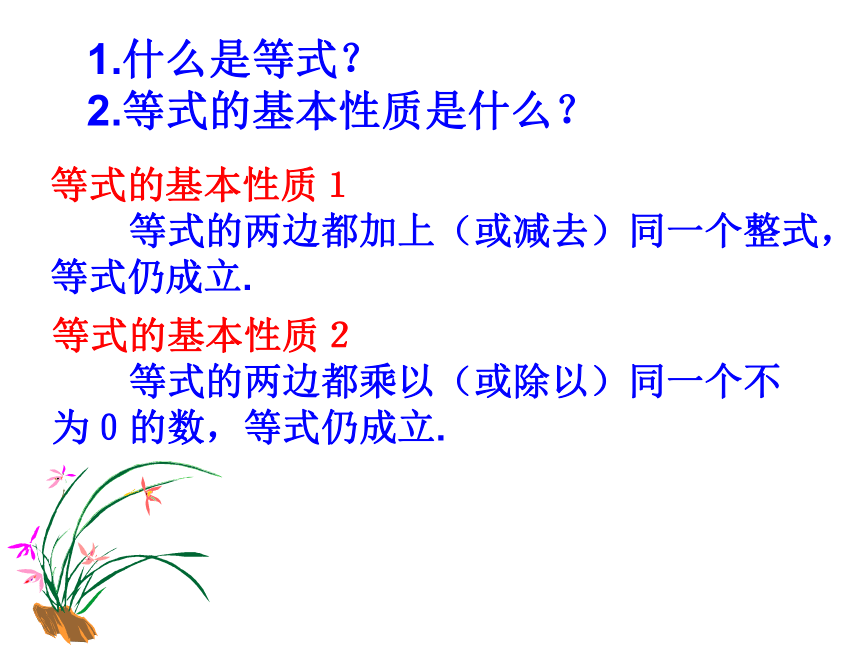
课件24张PPT。1.什么是等式？
2.等式的基本性质是什么？等式的基本性质１
　　等式的两边都加上（或减去）同一个整式，等式仍成立.
等式的基本性质２
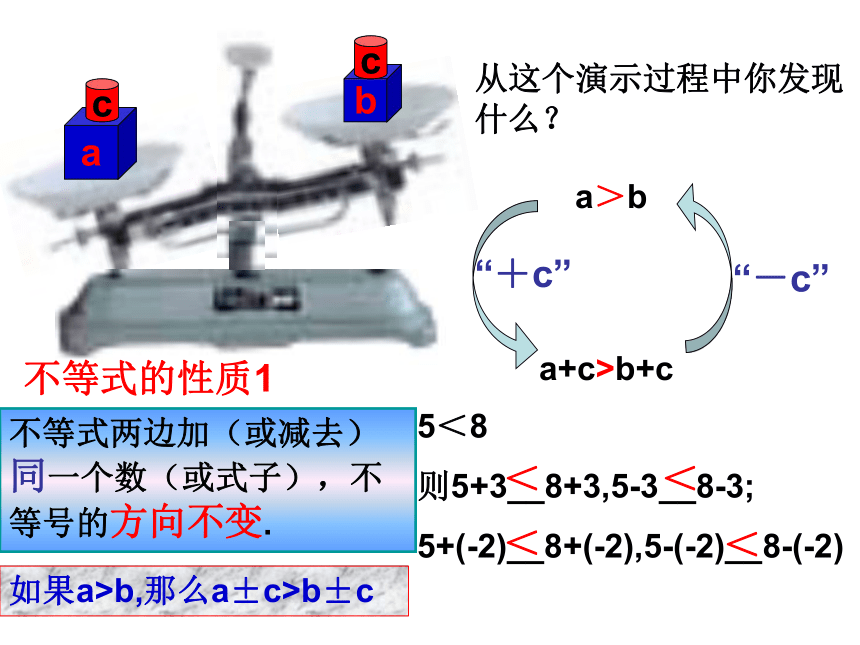
　　等式的两边都乘以（或除以）同一个不为０的数，等式仍成立.9.1.2不等式的性质（1）abcca＞ba+c>b+c“＋c”“－c”从这个演示过程中你发现什么？5＜8　
则5+3__8+3,5-3__8-3;
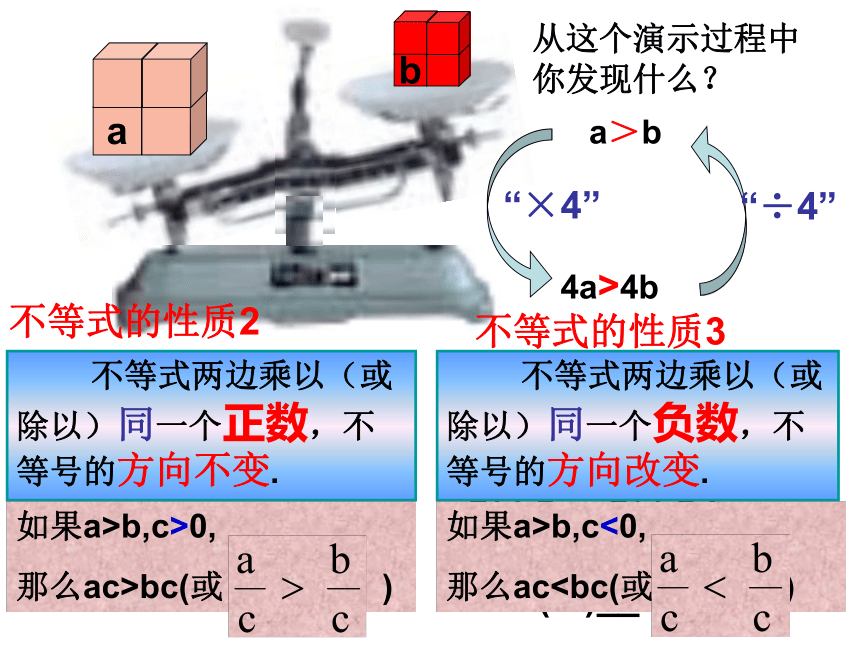
5+(-2)__8+(-2),5-(-2)__8-(-2)不等式两边加（或减去）同一个数（或式子），不等号的方向不变.不等式的性质1＜＜＜＜如果a>b,那么a±c>b±cb从这个演示过程中你发现什么？a＞b4a>4ba“×4”“÷4” 不等式两边乘以（或除以）同一个正数，不等号的方向不变.不等式的性质2如果a>b,c>0,
那么ac>bc(或 )＜＜5× (-３)__8× (-３),
5× (-2)__8× (-2)5＜8　
则5×3__8×3,
5×２__8×２;＞＞ 不等式两边乘以（或除以）同一个负数，不等号的方向改变.不等式的性质3如果a>b,c<0,
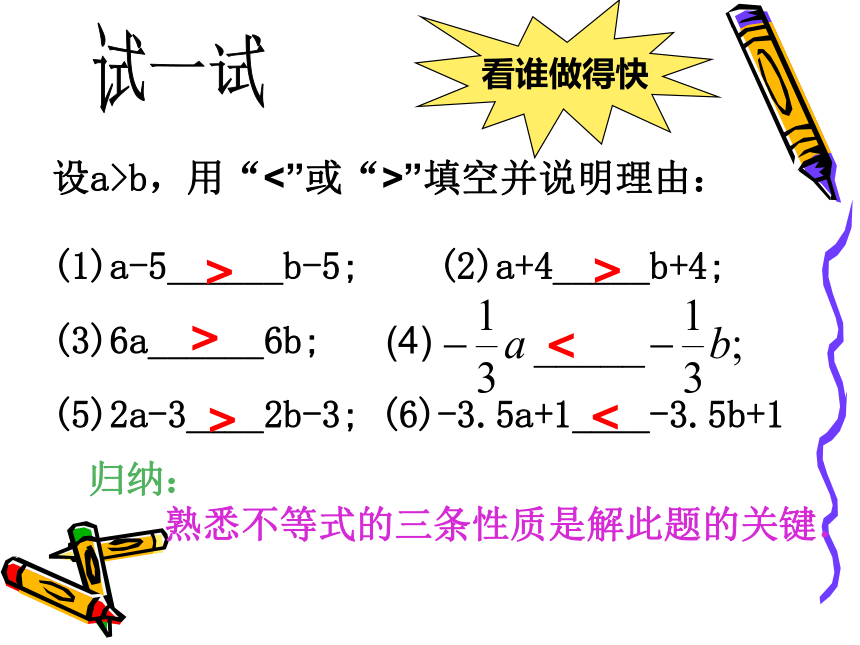
那么acb，用“<”或“>”填空并说明理由：
(1)a-5______b-5; (2)a+4_____b+4;>>><(3)6a______6b; (4)(5)2a-3____2b-3; (6)-3.5a+1____-3.5b+1><试一试 看谁做得快归纳：
　　熟悉不等式的三条性质是解此题的关键．例：利用不等式性质解下列不等式，并在数轴上表示解集：解一解（1）不等式两边同加上7得：
X-7+7>26+7
∴x>33(３)不等式两边同除以 2/３，得：
　x＞７５
解:(1)x-7>26; (2)3x<2x+1;(4)-4x>3(3)（５）x-１≤3x＋１１
1.用“＞”或“＜”在横线上填空，并在题后
括号内填写理由.
∵a＞b (2)∵ a＞b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m＞5n (4)∵4x＞5x
∴ -m ( ) ∴ x 0( )
(5)∵ ＜ (6)∵a-1＜8
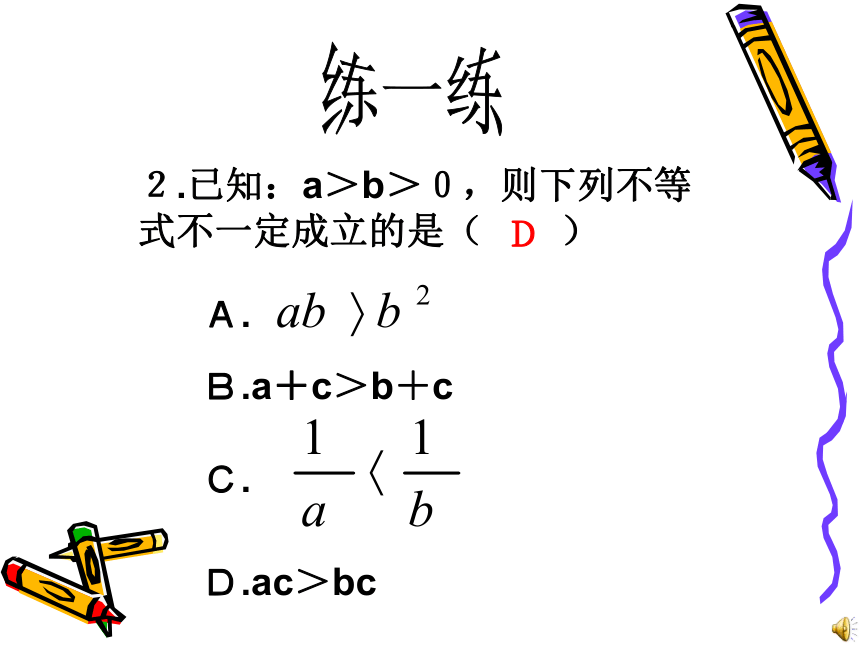
∴ a 2b( ) ∴ a 9( ) 练一练练一练２.已知：a＞b＞０，则下列不等式不一定成立的是（　　）Ａ.Ｂ.a＋c＞b＋cＤ.ac＞bcＣ.Ｄ练一练３.若a＞b，且c为有理数，则（　　）Ａ.ac＞bcＢ. ac＜bc Ｃ.Ｄ
４.由 x＞y 得 ax＞ay 的条件是（ ）
A.a＞0 B.a＜0 C.a≥0 D.a≤0
练一练Ａ
５.由 x＞y 得 ax≤ay 的条件是（ ）
A.a＞0 B.a＜0 C.a≥0 D.a≤0
练一练Ｄ６.由 a＞b 得 am2＞bm2 的条件是（ ）
A.m＞0 B.m＜0
C.m≠0 D.m是任意有理数
练一练Ｃ７.若 a＞1，则下列各式中错误的是（ ）
　A.4a＞4 　　　　 B.a+5＞6
C. 　＜ 　　　D.a-1＜0D练一练练一练8.用不等式的性质解下列不等式，并在数轴上表示解集：
(1)x+5>-1； (2)4x≤3x-5;
(4)-8x≥10
应用生活　　某服装商店以１５０元的价格购进一件服装，如果该商店以x元的价格出售，可获得大于４０﹪的利润.请用不等式表示该问题中的不等关系，然后利用不等式的基本性质说明：能否得到x的取值范围为“x＞２１０”？　　解：由题意，得：
X－１５０＞１５０×４０﹪∴x＞２１０即X－１５０＞６０（2）已知关于x的不等式（1－a）x＞2的解集
为 　　　 ，则a的取值范围是（　 ）
（A）a＞0　（B）a＞1　（C）a＜0　（D）a<1B思考题＜（3）已知有理数a、b、c在数轴上对应的点如图所示，则下列式子中 ① c+b>a+b ②-c+a>-b+a
③cbab 正确的个数有( )

（A）0 个 (B) 1 个 (C)2个 (D) 3个 B思考题园丁指路? 反思归纳 通过本节课的交流探究，你有哪些收获？一： 1.不等式的性质1、2、3.二：通过合作学习，体会从特殊到一般、数形结合、类比、化归等数学思想，同时感受到成功的喜悦. 2.等式性质与不等式性质的不同之处；
3.在运用“不等式性质3”时应注意的问题.１.比较３x与２x的大小知识拓展２.设x＞y，试比较代数式－（８－１０x）与－（８－１０y）的大小，如果较大的代数式为正数，则其中最小的正数x或y的值是多少？１.某供电公司为了鼓励市民用电，制定了如下标准收取电费：若每户每月用电不超过１００ＫＷ·h，则每千瓦时电收费０.５元；若每户每月用电超过１００ＫＷ·h，则超出部分每千瓦时电收费０.４元.小颖叫某月的电费不多于８０元，那么她家这个月的用电量最多是多少？课后思考１.某供电公司为了鼓励市民用电，制定了如下标准收取电费：若每户每月用电不超过１００ＫＷ·h，则每千瓦时电收费０.５元；若每户每月用电超过１００ＫＷ·h，则超出部分每千瓦时电收费０.４元.小颖叫某月的电费不多于８０元，那么她家这个月的用电量最多是多少？课后思考解：小颖家这个月用电量是xＫＷ·h，根据题意，得：０.５×１００＋０.４（x－１００）≤８０∴０.４x＋１０≤８０∴x≤１７５答：小颖家这个月用电量最多１７５ＫＷ·h.２.某商场计划投入一笔资金采购一批紧俏商品，经过市场调查发现，如果月初出售，可获利15％，并可用本和利再投资其他商品，到月末又可获利10％；如果月末出售可获利30％，但要付出仓库储费700元。请问根据商场的资金情况，如何购销获利较多？课后思考作业： 作业本及书本习题9.1 再见