1.1空间向量及其运算(第一课时)课件(共23张PPT)-2023-2024学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.1空间向量及其运算(第一课时)课件(共23张PPT)-2023-2024学年高二上学期数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 21:29:30 | ||
图片预览






文档简介
(共23张PPT)
1.1空间向量及其运算
——(第一课时)
复习导入
平面向量的概念
定义
既有大小又有方向的量叫做向量
长度/模
向量的大小叫做向量的长度(或模)
表示法
几何表示法
字母表示法
用有向线段表示。
A
B
C
D
用小写字母、等表示,或者用表示向量的有向线段的起点和终点字母表示。
复习导入
几类特殊的平面向量
零向量
单位向量
相等向量
相反向量
规定长度为的向量叫零向量,记为
模长为的的向量叫单位向量
长度相等且方向相同的向量
长度相等且方向相反的向量,的相反向量,记为
共线向量
方向相同或相反的非零向量
规定:零向量与任意向量平行,即对于任意向量,都有
复习导入
平面向量的线性运算
加法
减法
数乘
+
+
三角形法则
平行四边形法则
三角形法则
①
②当时,与同向;
当时,;
当时,与向.
加法交换律:
加法结合律:
数乘分配律:
新知探究
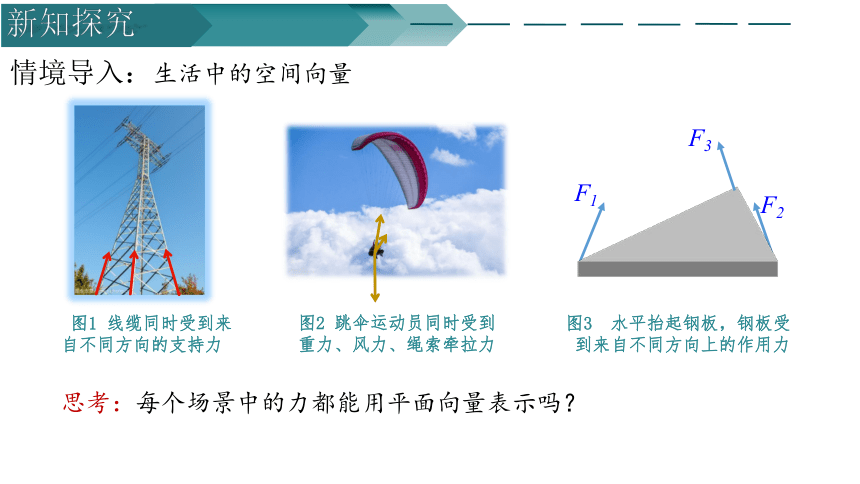
情境导入:生活中的空间向量
F1
F2
F3
图1 线缆同时受到来
自不同方向的支持力
图2 跳伞运动员同时受到
重力、风力、绳索牵拉力
图3 水平抬起钢板,钢板受
到来自不同方向上的作用力
思考:每个场景中的力都能用平面向量表示吗?
新知探究
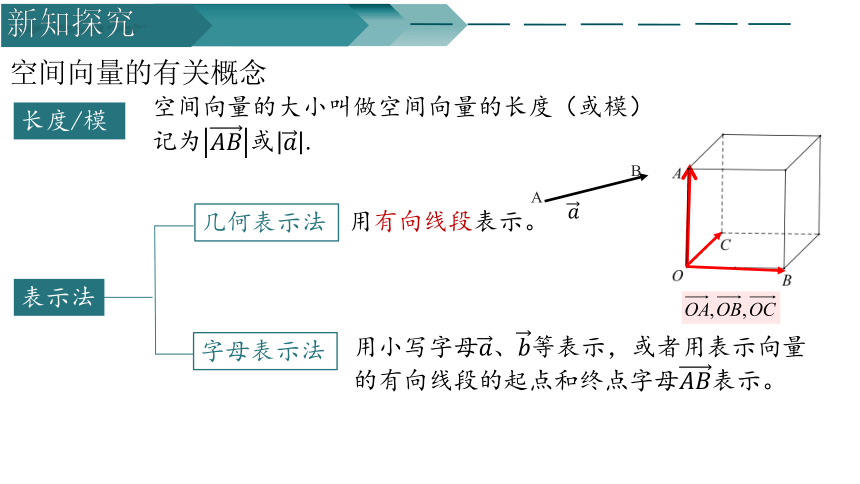
空间向量的有关概念
定义
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量。
类比平面向量,你能给出空间向量的有关概念吗?
新知探究
空间向量的有关概念
长度/模
空间向量的大小叫做空间向量的长度(或模)记为.
表示法
几何表示法
字母表示法
用有向线段表示。
用小写字母、等表示,或者用表示向量的有向线段的起点和终点字母表示。
A
B
新知探究
空间向量的有关概念
零向量
单位向量
相等向量
相反向量
规定长度为的向量叫零向量,记为
模长为的的向量叫单位向量
长度相等且方向相同的向量
长度相等且方向相反的向量,的相反向量,记为
共线向量
表示若干空间向量的有向线段所在直线平行或重合
规定:零向量与任意向量平行,即对于任意向量,都有
新知探究
辨析.判断正误.
(1)空间两个向量方向相反时,它们互为相反向量( )
(2)若空间两个向量相等,则它们方向相同,且起点相同( )
(3)若空间两个向量起点相同且长度相等,则这两个向量相等( )
(4)将空间所有单位向量平移到同一个起点,则它们的终点构成一个圆( )
(2)× 空间向量可平行移动,相等向量起点可以不同.
(3)× 缺少另一条件:方向相同.
(1)× 缺少另一条件:长度相等.
(4)× 它们的终点构成一个球面.
新知探究
空间向量的有关概念
思考:空间向量是如何运算的呢?与平面向量的运算有什么关系吗?
a
b
a
b
O
A
B
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,这样任意两个空间向量的运算,都可以转化为平面向量的运算.
新知探究
空间向量的有关概念
由此,我们把平面向量的线性运算推广到空间,定义空间向量的加法、减法(如图)以及数乘运算(如图):
(1)
(2)
(3)当时,
当时,
当时,
新知探究
空间向量的有关概念
与平面向量一样,空间向量的线性运算满足以下运算律(其中):
交换律:
结合律:
分配律:
b
c
a
a + b + c
a + b
b
a
a + b + c
b + c
c
新知探究
练一练:如图,已知平行六面体,化简下列向量表达式,并标出化简结果的向量.
A
B
C
D
A1
B1
C1
D1
(1)
(2)
(3)
(4)
一般地,对于三个不共面的向量以任意点为起点,为邻边作平行六面体,则的和等于以为起点的平行六面体对角线所表示的向量
新知探究
练一练:如图,已知空间四边形中,向量 , ,若为的中点,为的重心,试用, , 表示下列向量:
(1) ; (2) .
A
M
C
G
D
B
新知探究
空间向量的共线向量定理
共线向量定理:类似于平面向量共线的充要条件,对任意两个空间向量,,的充要条件是存在实数,使.
新知探究
方向向量
是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.
我们把与向量平行的非零向量称为直线的方向向量
新知探究
共面向量
注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,
也可能不共面.
d
b
a
c
共面向量:平行于同一平面的向量,叫做共面向量.
新知探究
空间向量的共面向量定理
共面向量定理:如果两个向量不共线,那么向量与共面的充要条件是存在唯一的有序实数对,使.
b
思考:定理中符合条件的有序实数对(x, y)为什么存在?又为什么唯一?
例1:如图,已知平行四边形,过平面外一点作射线,,,,在四条射线上分别取点,,,,使.求证:,,,四点共面.
证明:因为,
所以
因为四边形是平行四边形,所以
因此
由向量共面的充要条件可知,,共面,又
过同一点,从而,,,四点共面.
例题讲解
方法总结
、、三点共线
、、、 点共面
练习1:如图,已知,,,分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:,,,四点共面.
证明:如图,连接EG,BG.
因为=+=+(+)=++=+,
由向量共面的充要条件可知,向量,,共面,
又,,过同一点E,从而E,F,G,H四点共面.
从而,,,四点共面.
练习巩固
练习2:已知为空间任意一点,,,,四点共面,但任意三点不共线,如果,则的值为____________
【答案】
,
因为为空间任意一点,满足任意三点不共线,且四点共面,
所以,故.
练习巩固
练习3:已知点在确定的平面内,是平面外任意一点,实数满足,则的最小值为____________
【答案】
因为,点在确定的平面内,
所以,即,所以,
所以当时,的有最小值2.
小结
空间向量及其线性运算
空间向量
常见的空间向量
线性运算
共面向量
共线向量
定义、长度(模)、表示法
零向量、单位向量、相等向量、相反向量
加法、减法、数乘
1.1空间向量及其运算
——(第一课时)
复习导入
平面向量的概念
定义
既有大小又有方向的量叫做向量
长度/模
向量的大小叫做向量的长度(或模)
表示法
几何表示法
字母表示法
用有向线段表示。
A
B
C
D
用小写字母、等表示,或者用表示向量的有向线段的起点和终点字母表示。
复习导入
几类特殊的平面向量
零向量
单位向量
相等向量
相反向量
规定长度为的向量叫零向量,记为
模长为的的向量叫单位向量
长度相等且方向相同的向量
长度相等且方向相反的向量,的相反向量,记为
共线向量
方向相同或相反的非零向量
规定:零向量与任意向量平行,即对于任意向量,都有
复习导入
平面向量的线性运算
加法
减法
数乘
+
+
三角形法则
平行四边形法则
三角形法则
①
②当时,与同向;
当时,;
当时,与向.
加法交换律:
加法结合律:
数乘分配律:
新知探究
情境导入:生活中的空间向量
F1
F2
F3
图1 线缆同时受到来
自不同方向的支持力
图2 跳伞运动员同时受到
重力、风力、绳索牵拉力
图3 水平抬起钢板,钢板受
到来自不同方向上的作用力
思考:每个场景中的力都能用平面向量表示吗?
新知探究
空间向量的有关概念
定义
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量。
类比平面向量,你能给出空间向量的有关概念吗?
新知探究
空间向量的有关概念
长度/模
空间向量的大小叫做空间向量的长度(或模)记为.
表示法
几何表示法
字母表示法
用有向线段表示。
用小写字母、等表示,或者用表示向量的有向线段的起点和终点字母表示。
A
B
新知探究
空间向量的有关概念
零向量
单位向量
相等向量
相反向量
规定长度为的向量叫零向量,记为
模长为的的向量叫单位向量
长度相等且方向相同的向量
长度相等且方向相反的向量,的相反向量,记为
共线向量
表示若干空间向量的有向线段所在直线平行或重合
规定:零向量与任意向量平行,即对于任意向量,都有
新知探究
辨析.判断正误.
(1)空间两个向量方向相反时,它们互为相反向量( )
(2)若空间两个向量相等,则它们方向相同,且起点相同( )
(3)若空间两个向量起点相同且长度相等,则这两个向量相等( )
(4)将空间所有单位向量平移到同一个起点,则它们的终点构成一个圆( )
(2)× 空间向量可平行移动,相等向量起点可以不同.
(3)× 缺少另一条件:方向相同.
(1)× 缺少另一条件:长度相等.
(4)× 它们的终点构成一个球面.
新知探究
空间向量的有关概念
思考:空间向量是如何运算的呢?与平面向量的运算有什么关系吗?
a
b
a
b
O
A
B
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,这样任意两个空间向量的运算,都可以转化为平面向量的运算.
新知探究
空间向量的有关概念
由此,我们把平面向量的线性运算推广到空间,定义空间向量的加法、减法(如图)以及数乘运算(如图):
(1)
(2)
(3)当时,
当时,
当时,
新知探究
空间向量的有关概念
与平面向量一样,空间向量的线性运算满足以下运算律(其中):
交换律:
结合律:
分配律:
b
c
a
a + b + c
a + b
b
a
a + b + c
b + c
c
新知探究
练一练:如图,已知平行六面体,化简下列向量表达式,并标出化简结果的向量.
A
B
C
D
A1
B1
C1
D1
(1)
(2)
(3)
(4)
一般地,对于三个不共面的向量以任意点为起点,为邻边作平行六面体,则的和等于以为起点的平行六面体对角线所表示的向量
新知探究
练一练:如图,已知空间四边形中,向量 , ,若为的中点,为的重心,试用, , 表示下列向量:
(1) ; (2) .
A
M
C
G
D
B
新知探究
空间向量的共线向量定理
共线向量定理:类似于平面向量共线的充要条件,对任意两个空间向量,,的充要条件是存在实数,使.
新知探究
方向向量
是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.
我们把与向量平行的非零向量称为直线的方向向量
新知探究
共面向量
注意:空间任意两个向量是共面的,但空间任意三个向量既可能共面,
也可能不共面.
d
b
a
c
共面向量:平行于同一平面的向量,叫做共面向量.
新知探究
空间向量的共面向量定理
共面向量定理:如果两个向量不共线,那么向量与共面的充要条件是存在唯一的有序实数对,使.
b
思考:定理中符合条件的有序实数对(x, y)为什么存在?又为什么唯一?
例1:如图,已知平行四边形,过平面外一点作射线,,,,在四条射线上分别取点,,,,使.求证:,,,四点共面.
证明:因为,
所以
因为四边形是平行四边形,所以
因此
由向量共面的充要条件可知,,共面,又
过同一点,从而,,,四点共面.
例题讲解
方法总结
、、三点共线
、、、 点共面
练习1:如图,已知,,,分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:,,,四点共面.
证明:如图,连接EG,BG.
因为=+=+(+)=++=+,
由向量共面的充要条件可知,向量,,共面,
又,,过同一点E,从而E,F,G,H四点共面.
从而,,,四点共面.
练习巩固
练习2:已知为空间任意一点,,,,四点共面,但任意三点不共线,如果,则的值为____________
【答案】
,
因为为空间任意一点,满足任意三点不共线,且四点共面,
所以,故.
练习巩固
练习3:已知点在确定的平面内,是平面外任意一点,实数满足,则的最小值为____________
【答案】
因为,点在确定的平面内,
所以,即,所以,
所以当时,的有最小值2.
小结
空间向量及其线性运算
空间向量
常见的空间向量
线性运算
共面向量
共线向量
定义、长度(模)、表示法
零向量、单位向量、相等向量、相反向量
加法、减法、数乘
