2023-2024学年青岛版数学九年级上册1.2.2相似三角形的判定1 课件 16张PPT
文档属性
| 名称 | 2023-2024学年青岛版数学九年级上册1.2.2相似三角形的判定1 课件 16张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 678.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-31 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1.2.2相似三角形的判定1
PART 1
相似三角形
01
相似比
02
回顾
两个三角形,如果一个三角形的各个角与另一个三角形的各个角对应相等,各边对应成比例,那么这两个三角形叫做相似三角形
相似多边形对应边的比叫做相似比
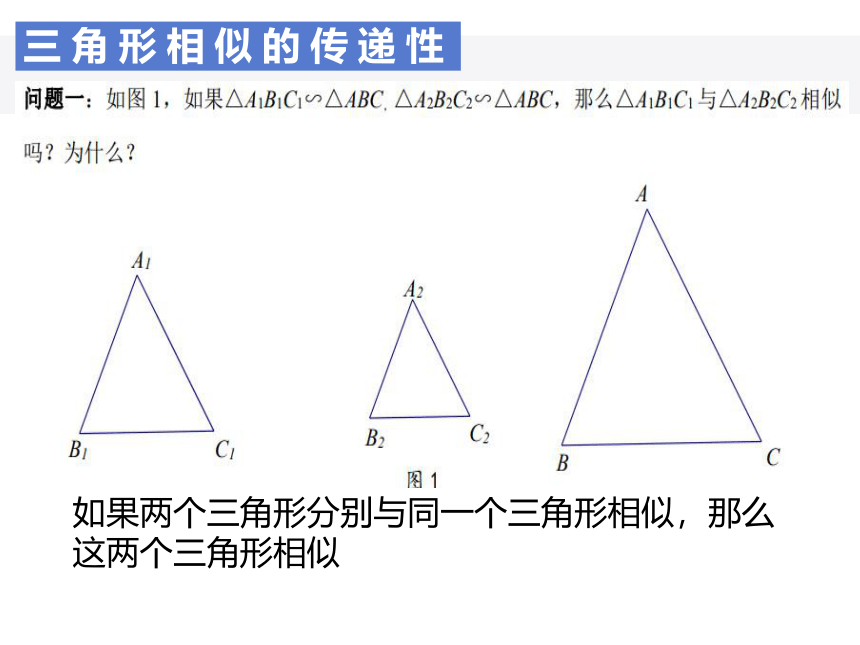
三角形相似的传递性
如果两个三角形分别与同一个三角形相似,那么这两个三角形相似
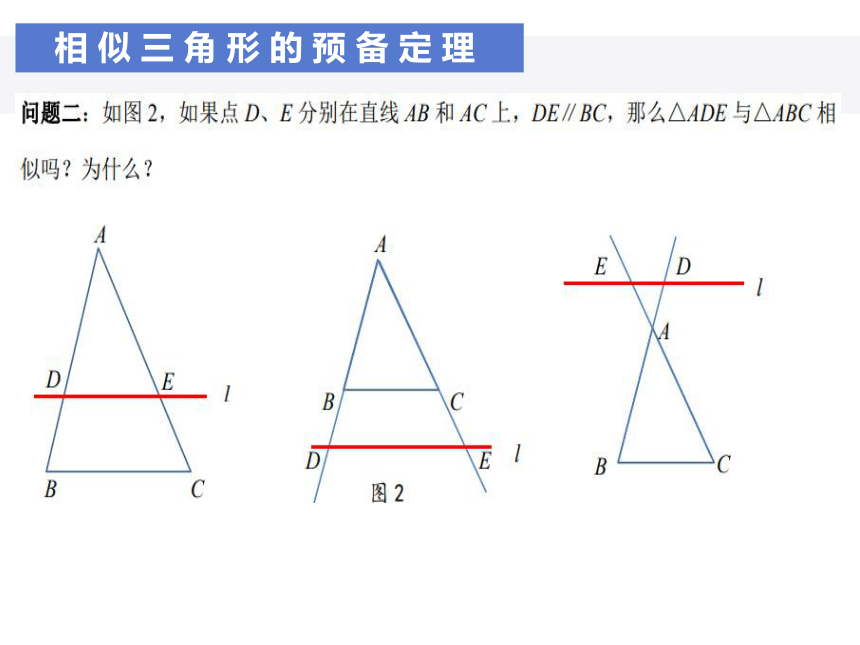
相似三角形的预备定理
相似三角形的预备定理
相似三角形的预备定理:平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似
平行法
几何语言:
∵DE∥BC
∴△ADE∽△ABC
B
C
D
E
A
A
B
C
D
E
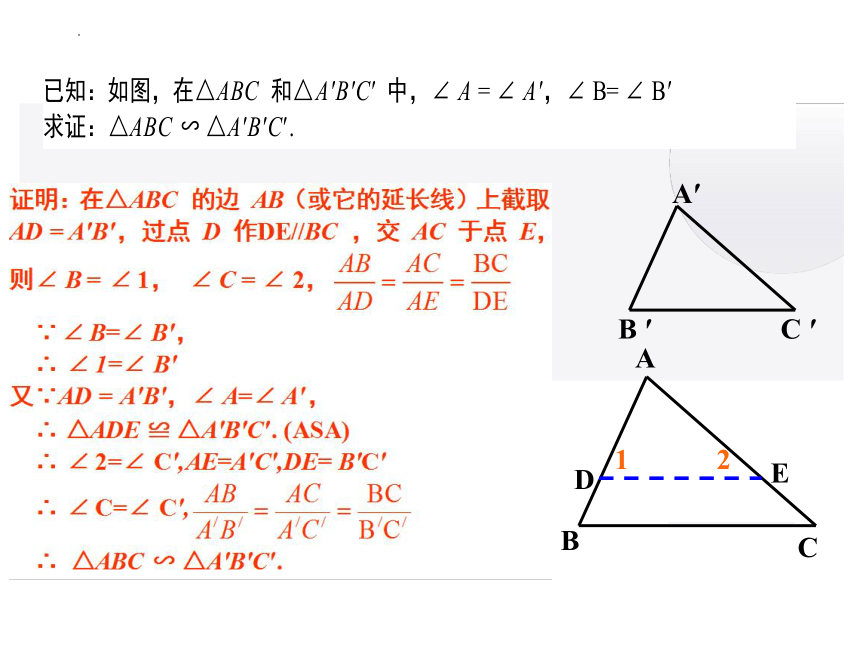
相似三角形判定定理1
C
A
B
A′
B ′
C ′
D
E
C
A
B
A′
B ′
C ′
D
E
1
2
相似三角形判定定理1
C
A
B
A′
B ′
C ′
D
E
如果一个三角形的两角与另外一个三角形的两角对应相等,那么这两个三角形相似
两角对应相等,两个三角形相似
例题
例1、已知:如图,∠ACB=∠AED。
找出图中所有相似的三角形。
A
B
C
D
E
O
例题精讲
解:△ABC∽△ADE, △BOE∽△DOC.
理由:∵ ∠ACB=∠AED
∠A=∠A
∴△ABC∽△ADE
∴∠B=∠D
∵∠BOE=∠DOC
∴△BOE∽△DOC.
例题
例2、已知:如图,在Rt△ABC中,∠C=90°,CD⊥AB垂足为D.找出图中所有相似的三角形.
┏
┏
D
C
B
A
△ABC∽△ACD
△ABC∽△CBD
△ACD∽△CBD
能否证:AC2=AD●AB
挑战自我
△ABD∽△ACE
△CDF∽△CAE
△CDF∽△BDA
△BEF∽△CDF
△BEF∽△BDA
△BEF∽△CEA
练习
1.下列说法:①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③一个三角形的两个内角分别是40°,65°,另一个三角形的两个内角分别是65°,75°,这两个三角形不相似;④有一个角为60°的两个直角三角形相似.其中正确的说法是 ( )A.②④ B.①③ C.①②④ D.②③④
训练点 相似三角形的判定定理1
提示:在判定两个三角形相似时,若知道两对角的度数或角之间的关系,通常利用三角形内角和定理找出两对角相等来判定两个三角形相似.
练习
2.如图,点D,E分别在△ABC的边AB,AC上,且∠1=∠2=∠B,则图中相似三角形有 ( ) A.1对 B.2对 C.3对 D.4对
解析:∵∠1=∠B,∠DAE=∠BAC,∴△ADE∽△ABC;∵∠2=∠B,∠CAD=∠BAC,∴△ACD∽△ABC,∴△ADE∽△ACD;∵∠1=∠B,∴DE∥BC,∴∠BCD=∠CDE.又∵∠B=∠2,∴△BCD∽△CDE.故选D.
练习
3.如图,∠ABD=∠C,AD=2,AC=8,则AB的长为________.
解析:∵∠BAD=∠CAB,∠ABD=∠C,∴△ABD∽△ACB,∴ ,∴AB2=AD·AC.∵AD=2,AC=8,∴AB=4.故答案为:4.
4
练习
4.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,过点A作AE⊥BD,垂足为点E.(1)求证:△ABE∽△DBC;(2)求线段AE的长.
解:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB.∵AD∥BC,∴∠ADB=∠DBC,∴∠ABE=∠DBC.∵AE⊥BD,∴∠AEB=∠C=90°,∴△ABE∽△DBC.(2)∵AB=AD,AE⊥BD,∴BE=DE,即BD=2BE.由△ABE∽△DBC,得 .∵AB=AD=25,BC=32,∴ ,∴BE=20,∴AE= =15.
THANKS
1.2.2相似三角形的判定1
PART 1
相似三角形
01
相似比
02
回顾
两个三角形,如果一个三角形的各个角与另一个三角形的各个角对应相等,各边对应成比例,那么这两个三角形叫做相似三角形
相似多边形对应边的比叫做相似比
三角形相似的传递性
如果两个三角形分别与同一个三角形相似,那么这两个三角形相似
相似三角形的预备定理
相似三角形的预备定理
相似三角形的预备定理:平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似
平行法
几何语言:
∵DE∥BC
∴△ADE∽△ABC
B
C
D
E
A
A
B
C
D
E
相似三角形判定定理1
C
A
B
A′
B ′
C ′
D
E
C
A
B
A′
B ′
C ′
D
E
1
2
相似三角形判定定理1
C
A
B
A′
B ′
C ′
D
E
如果一个三角形的两角与另外一个三角形的两角对应相等,那么这两个三角形相似
两角对应相等,两个三角形相似
例题
例1、已知:如图,∠ACB=∠AED。
找出图中所有相似的三角形。
A
B
C
D
E
O
例题精讲
解:△ABC∽△ADE, △BOE∽△DOC.
理由:∵ ∠ACB=∠AED
∠A=∠A
∴△ABC∽△ADE
∴∠B=∠D
∵∠BOE=∠DOC
∴△BOE∽△DOC.
例题
例2、已知:如图,在Rt△ABC中,∠C=90°,CD⊥AB垂足为D.找出图中所有相似的三角形.
┏
┏
D
C
B
A
△ABC∽△ACD
△ABC∽△CBD
△ACD∽△CBD
能否证:AC2=AD●AB
挑战自我
△ABD∽△ACE
△CDF∽△CAE
△CDF∽△BDA
△BEF∽△CDF
△BEF∽△BDA
△BEF∽△CEA
练习
1.下列说法:①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③一个三角形的两个内角分别是40°,65°,另一个三角形的两个内角分别是65°,75°,这两个三角形不相似;④有一个角为60°的两个直角三角形相似.其中正确的说法是 ( )A.②④ B.①③ C.①②④ D.②③④
训练点 相似三角形的判定定理1
提示:在判定两个三角形相似时,若知道两对角的度数或角之间的关系,通常利用三角形内角和定理找出两对角相等来判定两个三角形相似.
练习
2.如图,点D,E分别在△ABC的边AB,AC上,且∠1=∠2=∠B,则图中相似三角形有 ( ) A.1对 B.2对 C.3对 D.4对
解析:∵∠1=∠B,∠DAE=∠BAC,∴△ADE∽△ABC;∵∠2=∠B,∠CAD=∠BAC,∴△ACD∽△ABC,∴△ADE∽△ACD;∵∠1=∠B,∴DE∥BC,∴∠BCD=∠CDE.又∵∠B=∠2,∴△BCD∽△CDE.故选D.
练习
3.如图,∠ABD=∠C,AD=2,AC=8,则AB的长为________.
解析:∵∠BAD=∠CAB,∠ABD=∠C,∴△ABD∽△ACB,∴ ,∴AB2=AD·AC.∵AD=2,AC=8,∴AB=4.故答案为:4.
4
练习
4.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,过点A作AE⊥BD,垂足为点E.(1)求证:△ABE∽△DBC;(2)求线段AE的长.
解:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB.∵AD∥BC,∴∠ADB=∠DBC,∴∠ABE=∠DBC.∵AE⊥BD,∴∠AEB=∠C=90°,∴△ABE∽△DBC.(2)∵AB=AD,AE⊥BD,∴BE=DE,即BD=2BE.由△ABE∽△DBC,得 .∵AB=AD=25,BC=32,∴ ,∴BE=20,∴AE= =15.
THANKS
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
