22.3实际问题与二次函数-2023-2024学年人教版九年级数学上册同步练习(含答案)
文档属性
| 名称 | 22.3实际问题与二次函数-2023-2024学年人教版九年级数学上册同步练习(含答案) | 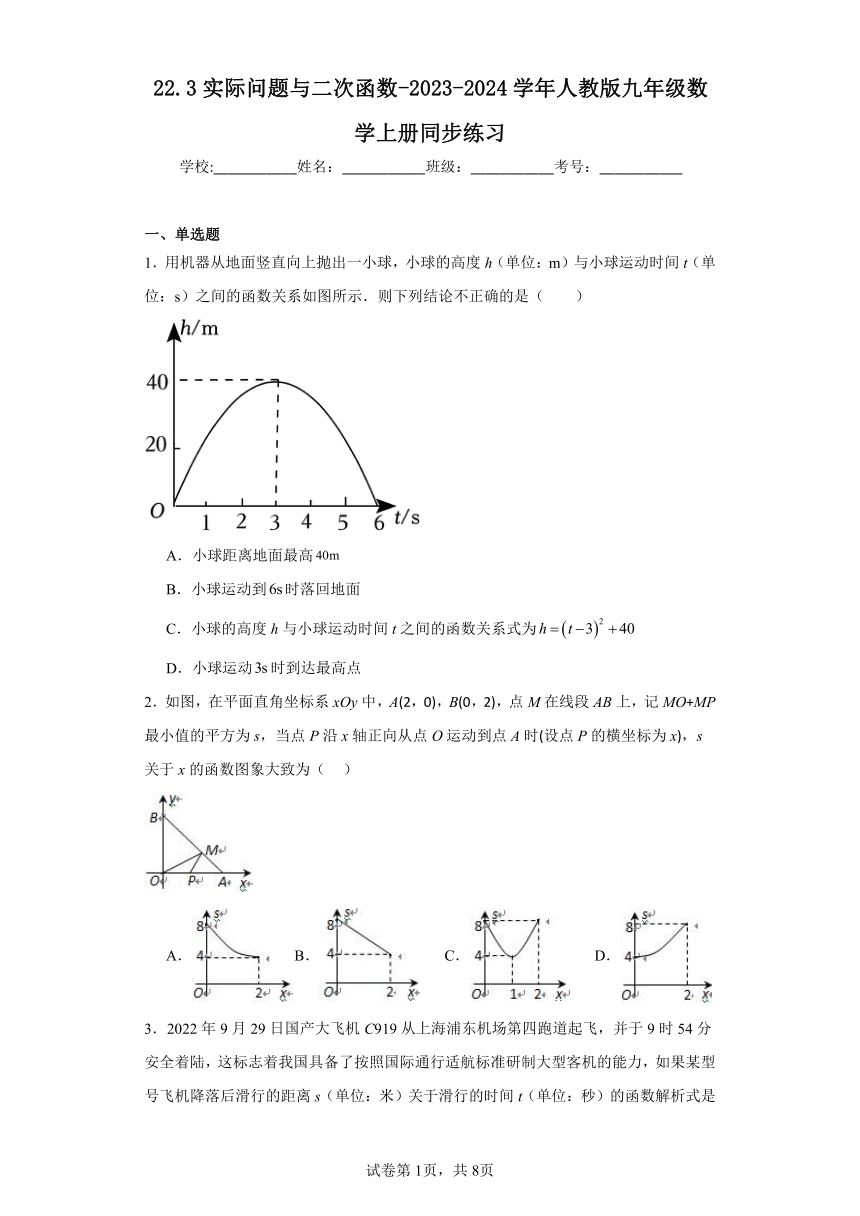 | |
| 格式 | docx | ||
| 文件大小 | 430.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 14:45:35 | ||
图片预览




文档简介
22.3实际问题与二次函数-2023-2024学年人教版九年级数学上册同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用机器从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球距离地面最高
B.小球运动到时落回地面
C.小球的高度h与小球运动时间t之间的函数关系式为
D.小球运动时到达最高点
2.如图,在平面直角坐标系xOy中,A(2,0),B(0,2),点M在线段AB上,记MO+MP最小值的平方为s,当点P沿x轴正向从点O运动到点A时(设点P的横坐标为x),s关于x的函数图象大致为( )
A. B. C. D.
3.2022年9月29日国产大飞机C919从上海浦东机场第四跑道起飞,并于9时54分安全着陆,这标志着我国具备了按照国际通行适航标准研制大型客机的能力,如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则该飞机着陆后滑行最长时间为( )
A.243秒 B.486秒 C.18秒 D.36秒
4.如图(1)所示,E为矩形的边上一点,动点P,Q同时从点B出发,点P沿折线运动到点C时停止,点Q沿运动到点C时停止,它们运动的速度都是1cm/秒,设P,Q同时出发t秒时,的面积为.已知y与t的函数关系图像如图(2)(曲线为抛物线的一部分),则下列结论不正确的是( )
A. B.当秒时,
C.当时, D.当的面积为时,t的值是或秒
5.果农计划对果园加大种植密度,据测算,果园的总产量个与增种果树的棵数棵间的函数关系式为,要使总产量在60320个以上,需要增加果树的棵数范围是
A. B.或 C. D.或
6.如图所示,点P是边长为1的正方形对角线上一动点(P与点A、C不重合),点E在上,且,设,的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
A. B. C. D.
7.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
8.板球是以击球、投球和接球为主的运动,该项目主要锻炼手眼的协调能力,集上肢动作控制能力、技巧与力量为一体的综合性运动.如图,是运动员击球过程中板球运动的轨迹示意图,板球在点A处击出,落地前的点B处被对方接住,已知板球经过的路线是抛物线,其表达式为y=-x2+x+1,则板球运行中离地面的最大高度为( )
A.1m B.m C.m D.4m
9.如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线的一部分,则杯口的口径AC为( )
A.7 B.8 C.9 D.10
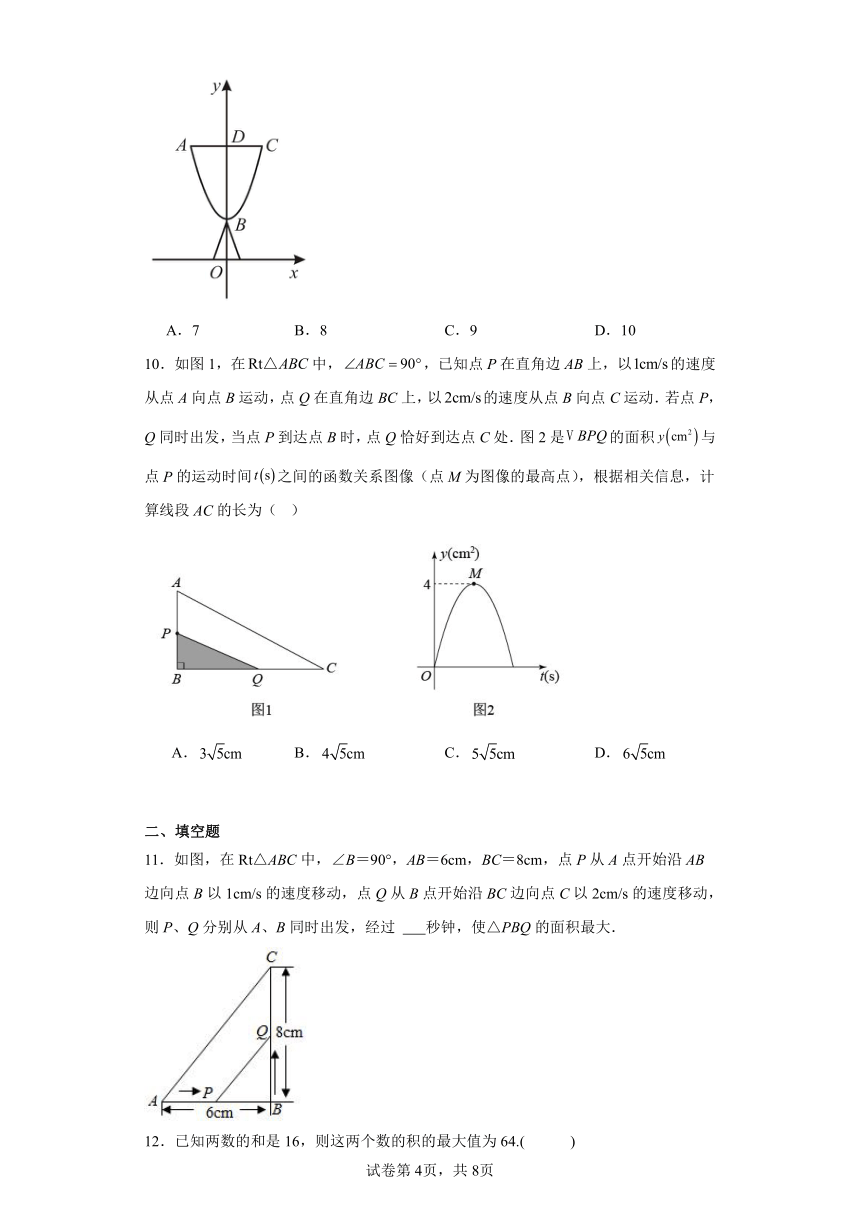
10.如图1,在中,,已知点P在直角边AB上,以的速度从点A向点B运动,点Q在直角边BC上,以的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处.图2是的面积与点P的运动时间之间的函数关系图像(点M为图像的最高点),根据相关信息,计算线段AC的长为( )
A. B. C. D.
二、填空题
11.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,则P、Q分别从A、B同时出发,经过 秒钟,使△PBQ的面积最大.
12.已知两数的和是16,则这两个数的积的最大值为64.( )
13.如图,抛物线y=x2-x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t
(1)点Q的横坐标是 (用含t的代数式表示);
(2)若⊙P与⊙Q 相离,则t的取值范围是
14.图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ,tanβ= ,以O为原点,OA所在直线为x轴建立直角坐标系,则点P到水面OA的距离是 m.
15.炮弹从炮口射出后,飞行的高度与飞行的时间之间的函数关系是,其中是炮弹发射的初速度,是炮弹的发射角,当, 时,炮弹飞行的最大高度是 .
16.烟花厂为建党100周年特别设计制作了一种新型礼炮,这种礼炮的升空高度与飞行时间的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为 .
17.超市销售的某商品进价10元/件.在销售过程中发现,该商品每天的销售量y(件)与售价x(元/件)之间满足函数关系式y=-5x+150,该商品售价定为 元/件时,每天销售该商品获利最大.
18.距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度(米)与物体运动的时间(秒)之间满足函数关系,其图像如图所示,物体运动的最高点离地面米,物体从发射到落地的运动时间为秒,设表示秒到秒时的值的“极差”(即秒到秒时的最大值与最小值的差).
(1) , ;
(2)当时,的取值范围是 .
19.某企业研发出了一种新产品准备销售,已知研发、生产这种产品的成本为30元/件,据调查年销售量y(万件)关于售价x(元/件)的函数解析式为: ,则当该产品的售价x为 .(元/件)时,企业销售该产品获得的年利润最大.
20.已知某商品销售利润(元)与该商品销售单价(个)满足,则该商品获利最多为 元.
三、解答题
21.某校九年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出100千克.
小强:如果以12元/千克的价格销售,那么每天可售出80千克.
小红:通过调查验证,我发现每天的销售量(千克)与销售单价(元)之间存在一次函数关系.
小强:我发现每天的销售量在70千克至100千克之间.
那么当销售单价为何值时,该超市销售这种水果每天获取的利润为320元?
22.中百仓储试销一种新型商品,经市场调查,该商品第天的进价(元/件)与(天)之间的相关信息如下表:
时间(天)
进价(元∕件) 40
该商品在销售过程中,日销售量(件)与(天)之间的函数关系如图所示.
在销售过程中,中百仓储每天以每件80元的价格将当天所进商品全部售出.
(1)求该商品的日销售量(件)与(天)之间的函数关系式;
(2)中百仓储在销售该商品的过程中,第几天的销售利润最大?最大日销售利润是多少?
23.某厂按用户的月需求量x (件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本为y (万元),y与x的关系式为(a,b为常数).经市场调研发现,月需求量x与月份n (n为整数,)的关系式为,且得到了下表中的数据.
月份n(月) 1 2
成本y(万元/件) 11 12
(1)请直接写出a,b的值;
(2)设第n个月的利润为W(万元),请求出W与n的函数关系式,并求出这一年的12个月中,哪个月份的利润为84万元;
(3)在这一年的前8个月中,哪个月的利润最大?最大利润是多少?
24.某景区超市销售一种纪念品,这种商品的成本价元件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于元件,市场调查发现,该商品每天当量件与销售单价元件之间的函数关系如图所示
(1)求与之间的函数关系式,并写出自变量x的取值范围:
(2)求每天的销售利润元与销售单价元件之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
25.小马同学在体育课上积极练习掷实心球,在练习过程中善于观察的他发现,实心球掷出后在空中的轨迹是一条抛物线,每个同学掷实心球的出手高度是一个固定值(身高米).如图,小马身高1.75米,设他抛出的实心球(记为点)到投掷点的水平距离为(单位:米),实心球(点)在空中的高度为(单位:米),与之间满足的函数表达式为.
(1)的值为________;
(2)当时,
①若实心球落地点为,此时,求小丁本次掷实心球的水平距离;
②落地点要超过,则的取值范围为________;
(3)已知男生掷实心球项目满分为10.30米,小马通过反复练习,使得自己掷出的实心球到投掷点的水平距离为4米时,恰好达到最大高度4米,你认为他能取得满分吗?请说明理由.(参考数据:,,,,)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.C
5.C
6.D
7.C
8.B
9.C
10.B
11.3
12.√
13. 5-t 0≤t<1,2<t≤
14.
15.1125m
16.
17.20
18. , , .
19.50
20.
21.销售单价为12元/千克时,该超市销售这种水果每天获取的利润为320元
22.(1)
(2)第25天的销售利润最大,最大利润为2450元
23.(1)a=6,b=300;(2)w=12n2-156n+564,5月份和8月份的利润均为84万元;(3)在这一年的前8个月中,1月的利润最大,最大利润是420万元.
24.(1);
(2)每件销售价为元时,每天的销售利润最大,最大利润是元
25.(1)2.4
(2)①;②
(3)能,理由见解析
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用机器从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球距离地面最高
B.小球运动到时落回地面
C.小球的高度h与小球运动时间t之间的函数关系式为
D.小球运动时到达最高点
2.如图,在平面直角坐标系xOy中,A(2,0),B(0,2),点M在线段AB上,记MO+MP最小值的平方为s,当点P沿x轴正向从点O运动到点A时(设点P的横坐标为x),s关于x的函数图象大致为( )
A. B. C. D.
3.2022年9月29日国产大飞机C919从上海浦东机场第四跑道起飞,并于9时54分安全着陆,这标志着我国具备了按照国际通行适航标准研制大型客机的能力,如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则该飞机着陆后滑行最长时间为( )
A.243秒 B.486秒 C.18秒 D.36秒
4.如图(1)所示,E为矩形的边上一点,动点P,Q同时从点B出发,点P沿折线运动到点C时停止,点Q沿运动到点C时停止,它们运动的速度都是1cm/秒,设P,Q同时出发t秒时,的面积为.已知y与t的函数关系图像如图(2)(曲线为抛物线的一部分),则下列结论不正确的是( )
A. B.当秒时,
C.当时, D.当的面积为时,t的值是或秒
5.果农计划对果园加大种植密度,据测算,果园的总产量个与增种果树的棵数棵间的函数关系式为,要使总产量在60320个以上,需要增加果树的棵数范围是
A. B.或 C. D.或
6.如图所示,点P是边长为1的正方形对角线上一动点(P与点A、C不重合),点E在上,且,设,的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
A. B. C. D.
7.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
8.板球是以击球、投球和接球为主的运动,该项目主要锻炼手眼的协调能力,集上肢动作控制能力、技巧与力量为一体的综合性运动.如图,是运动员击球过程中板球运动的轨迹示意图,板球在点A处击出,落地前的点B处被对方接住,已知板球经过的路线是抛物线,其表达式为y=-x2+x+1,则板球运行中离地面的最大高度为( )
A.1m B.m C.m D.4m
9.如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线的一部分,则杯口的口径AC为( )
A.7 B.8 C.9 D.10
10.如图1,在中,,已知点P在直角边AB上,以的速度从点A向点B运动,点Q在直角边BC上,以的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处.图2是的面积与点P的运动时间之间的函数关系图像(点M为图像的最高点),根据相关信息,计算线段AC的长为( )
A. B. C. D.
二、填空题
11.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,则P、Q分别从A、B同时出发,经过 秒钟,使△PBQ的面积最大.
12.已知两数的和是16,则这两个数的积的最大值为64.( )
13.如图,抛物线y=x2-x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t
(1)点Q的横坐标是 (用含t的代数式表示);
(2)若⊙P与⊙Q 相离,则t的取值范围是
14.图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ,tanβ= ,以O为原点,OA所在直线为x轴建立直角坐标系,则点P到水面OA的距离是 m.
15.炮弹从炮口射出后,飞行的高度与飞行的时间之间的函数关系是,其中是炮弹发射的初速度,是炮弹的发射角,当, 时,炮弹飞行的最大高度是 .
16.烟花厂为建党100周年特别设计制作了一种新型礼炮,这种礼炮的升空高度与飞行时间的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为 .
17.超市销售的某商品进价10元/件.在销售过程中发现,该商品每天的销售量y(件)与售价x(元/件)之间满足函数关系式y=-5x+150,该商品售价定为 元/件时,每天销售该商品获利最大.
18.距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度(米)与物体运动的时间(秒)之间满足函数关系,其图像如图所示,物体运动的最高点离地面米,物体从发射到落地的运动时间为秒,设表示秒到秒时的值的“极差”(即秒到秒时的最大值与最小值的差).
(1) , ;
(2)当时,的取值范围是 .
19.某企业研发出了一种新产品准备销售,已知研发、生产这种产品的成本为30元/件,据调查年销售量y(万件)关于售价x(元/件)的函数解析式为: ,则当该产品的售价x为 .(元/件)时,企业销售该产品获得的年利润最大.
20.已知某商品销售利润(元)与该商品销售单价(个)满足,则该商品获利最多为 元.
三、解答题
21.某校九年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出100千克.
小强:如果以12元/千克的价格销售,那么每天可售出80千克.
小红:通过调查验证,我发现每天的销售量(千克)与销售单价(元)之间存在一次函数关系.
小强:我发现每天的销售量在70千克至100千克之间.
那么当销售单价为何值时,该超市销售这种水果每天获取的利润为320元?
22.中百仓储试销一种新型商品,经市场调查,该商品第天的进价(元/件)与(天)之间的相关信息如下表:
时间(天)
进价(元∕件) 40
该商品在销售过程中,日销售量(件)与(天)之间的函数关系如图所示.
在销售过程中,中百仓储每天以每件80元的价格将当天所进商品全部售出.
(1)求该商品的日销售量(件)与(天)之间的函数关系式;
(2)中百仓储在销售该商品的过程中,第几天的销售利润最大?最大日销售利润是多少?
23.某厂按用户的月需求量x (件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本为y (万元),y与x的关系式为(a,b为常数).经市场调研发现,月需求量x与月份n (n为整数,)的关系式为,且得到了下表中的数据.
月份n(月) 1 2
成本y(万元/件) 11 12
(1)请直接写出a,b的值;
(2)设第n个月的利润为W(万元),请求出W与n的函数关系式,并求出这一年的12个月中,哪个月份的利润为84万元;
(3)在这一年的前8个月中,哪个月的利润最大?最大利润是多少?
24.某景区超市销售一种纪念品,这种商品的成本价元件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于元件,市场调查发现,该商品每天当量件与销售单价元件之间的函数关系如图所示
(1)求与之间的函数关系式,并写出自变量x的取值范围:
(2)求每天的销售利润元与销售单价元件之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
25.小马同学在体育课上积极练习掷实心球,在练习过程中善于观察的他发现,实心球掷出后在空中的轨迹是一条抛物线,每个同学掷实心球的出手高度是一个固定值(身高米).如图,小马身高1.75米,设他抛出的实心球(记为点)到投掷点的水平距离为(单位:米),实心球(点)在空中的高度为(单位:米),与之间满足的函数表达式为.
(1)的值为________;
(2)当时,
①若实心球落地点为,此时,求小丁本次掷实心球的水平距离;
②落地点要超过,则的取值范围为________;
(3)已知男生掷实心球项目满分为10.30米,小马通过反复练习,使得自己掷出的实心球到投掷点的水平距离为4米时,恰好达到最大高度4米,你认为他能取得满分吗?请说明理由.(参考数据:,,,,)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.C
5.C
6.D
7.C
8.B
9.C
10.B
11.3
12.√
13. 5-t 0≤t<1,2<t≤
14.
15.1125m
16.
17.20
18. , , .
19.50
20.
21.销售单价为12元/千克时,该超市销售这种水果每天获取的利润为320元
22.(1)
(2)第25天的销售利润最大,最大利润为2450元
23.(1)a=6,b=300;(2)w=12n2-156n+564,5月份和8月份的利润均为84万元;(3)在这一年的前8个月中,1月的利润最大,最大利润是420万元.
24.(1);
(2)每件销售价为元时,每天的销售利润最大,最大利润是元
25.(1)2.4
(2)①;②
(3)能,理由见解析
答案第1页,共2页
答案第1页,共2页
同课章节目录
